贝叶斯理论在水文不确定性分析中的应用
周平朱仁义
(巢湖学院物理与电子科学系,安徽巢湖238000)
贝叶斯理论在水文不确定性分析中的应用
周平朱仁义
(巢湖学院物理与电子科学系,安徽巢湖238000)
本文简要介绍了贝叶斯理论的基本原理。阐述了贝叶斯理论在水文不确定性分析中的应用,包括在模型参数、模型结构、水文组合预报、区域洪水频率分析中的应用情况。并指出了贝叶斯理论在水文不确定性分析中的应用前景。
贝叶斯理论;不确定性;参数
水文过程是一个高度复杂的非线性过程,其发生、发展过程中受众多不确定性因素影响,本身呈现出随机、模糊、混沌、灰色和未确知等自然不确定性。而现有的水文模型都是采用数学物理方法对复杂水文过程的一种简化,使模拟的水文过程又受到水文输入、模型结构和模型参数不确定性的影响。
基于贝叶斯理论的水文不确定性分析,能将认知的先验信息和样本信息有效结合,以概率分布的形式描述水文不确定性。不仅可以给出水文变量的均值,还能给出其方差和指定概率的置信区间,描述水文变量发生的不确定性程度,比确定性水文模型描述水文过程更具合理性和科学性。基于贝叶斯理论的水文不确定性分析能使决策者将风险考虑到决策中去,实现水文分析与决策有机结合,更好地实现水文分析的作用,体现其价值。本文简述贝叶斯理论在水文不确定性分析中的应用现状,并指出其应用前景。
1 贝叶斯理论的基本原理
贝叶斯公式通常以事件形式或随机变量形式表示。
事件形式:设事件A1,A2,…,An互不相容,并且有(Ω为必然事件),则对任一事件Ai,有:

若以随机变量形式表示,为:

式中,x、y为随机变量,f(.)是随机变量的先验概率密度函数,一般根据经验知识确定是随机变量x、y间关系,在x已知的条件下,表示为y的条件概率密度,在y已知的情况下,表示为x的似然函数;已知(作为发生的样本)情况下,x的后验密度函数(又称验后密度函数);X为随机变量x的取值范围。当人们对变量x的先验没有任何信息时,认为x在它允许取值的范围内机会是相等的,即认为的先验分布f(.)在其值域上是均匀分布的。
2 贝叶斯理论在水文不确定性分析中应用
假设已获取容量为n的样本X=(x1,x2,…,xn),需估计与此样本有关的随机变量θ的概率密度,且假定在θ已知的情况下,样本X的出现的概率为。则基于贝叶斯公式(1)和式(2)的贝叶斯统计推断θ的后验密度π(θX)主要包括以下2个步骤[1-4]。
步骤1:根据参数θ的先验信息确定其先验分布π(θ)。
步骤2:确定θ的后验密度π(θX)。设h(θ,X)为θ和X的联合概率密度函数,则:

式中,m(X)为X的边缘密度函数,定义为:

由式(3)和式(4)得:
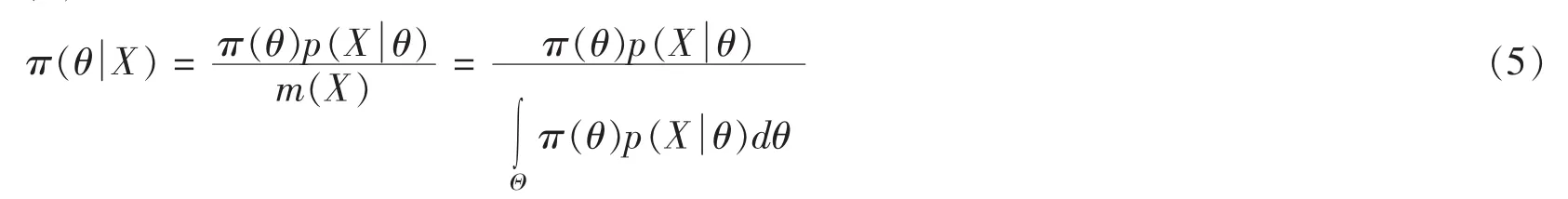
式中,p(X)为样本X=(x1,x2,…,xn)的联合概率密度函数。

正态分布似然函数表示如:

2.1 在水文模型参数不确定性分析中应用
水文模型参数反映的是流域水文特征,是一些原则上可以实测的物理量,但由于实际中往往难以做到,通常都是根据一定的测站资料,通过一定的目标函数,率定出一组“最佳参数”。由于资料的代表性、测量误差、目标函数的选取、计算方法的简化等局限性,一般只能得到局部最优参数,抑或出现“异参同效”现象,致使水文模型参数具有不确定性,导致根据此参数进行模拟和预测的水文过程具有不确定性。[5]
水文模型参数的后验估计,只需将式(5)中的变量θ作为模型参数即可。式(5)通常情况下难以用解析形式表达。因此,通常通过Monte Carlo随机模拟方法获得水文模型参数θ的后验密度估计。基于马尔可夫链蒙特卡罗法(MCMC)常被用来产生后验分布的概率密度函数。MCMC基本上是一种通过展开马氏链来获得相关样本的混合型蒙特卡罗方法。MCMC的关键是如何选择推荐分布(转移密度)使抽样更加有效。MCMC的性能很大程度上取决其采样的算法,常用的采样算法有Metropolis算法、Metropolis-Hastings算法、吉布斯(Gibbs)采样和Adapative Metropolis算法等[3,6,7]。
将通过MCMC方法抽样得到的模型参数θ带入模型,即可获得模拟样本,通过对大量的模拟样本进行统计分析,就可以得到模拟值或预报量的统计特征[5]。
2.2 在水文模型结构不确定性分析中应用
模型结构不确定性一般表现在两个方面,一是同一模型的不同子结构组成对预报结果产生的不确定性;二是采用不同模型给预报结果带来的不确定性。不同模型各具优缺点,若选择一个较优模型计算值的同时舍弃另外模型的计算值是不明智的,因为舍弃的模型计算值一般都蕴含某些有用的独立信息。不同的模型组合往往能得到较好的模拟或预报计算值。实现模型组合的方法有很多种,如以模型计算与实测数据的残差信息作为目标函数,采用组合权重法实现不同模型的组合;以不同模型的计算值作为神经网络的输入节点值,实测值作为网络的输出值,基于神经网络构建组合预测模型等。假定k个模型对实测X的组合预测值为Y,它们间的关系为,通常可以通过线性回归方法建立关系L或者将X、Y通过亚高斯模型实现正态分位数转换后再建立线性回归关系[2,8]。

若先验密度函数g(X)与似然函数L(X Y)均采用正态分布函数表示,即

则f(X Y)也服从正态分布,其均值E(X Y)和方差D(X Y)分别为[1,9]:

若先验密度和似然函数形式比较复杂,也可采用如神经网络等智能算法建立g(X)、L(XY)的函数关系[3]。
2.3 在区域洪水频率分析中应用
水文事件的总体是未知的。现行的洪水频率计算方法,运用概率统计的理论,用单站资料作为样本,对假设总体及参数进行统计推断。由于观测资料有限,在样本资料较短的情况下,由单站样本资料推求总体往往有较大的误差和任意性。提高洪水频率分析的精度方法主要有洪水分布线型和改进参数估计这两条途径。其中参数估计可以结合地区信息,以地区的区域化参数作为单站频率曲线的先验参数,结合单站资料进行参数的后验估计,可使推出的参数既含有单站信息也具有地区信息,增强估计参数的可靠性[1]。
若根据地区信息得到水文频率曲线参数θ的先验概率密度为g(θ),单站发生的样本为X=(x1,x2,…,xn),则参数θ的后验密度估计为:

参数θ的数学期望E(θ)为:

单站水文变量x的后验密度函数f′(x)为:

2.4 在洪水预报中应用
Roman Krzysztofwicz等人[6,7]基于贝叶斯概率水文预报理论(Bayesian Forecasting system),认为应采用概率分布定量地描述水文预报的不确定度;同时,决策者应当根据这个概率分布,而不是直接根据预报来制定决策。该预报理论已经获得广泛运用,其基本思路是:首先根据其特性和对水文预报的影响大小,将总不确定度分解成两大部分,即输入不确定度和水文不确定度,然后采用不同的方法进行处理。
以W表示模型输入,S表示输出,H表示预报变量,并以它们的小写字母w、s和h表示相应的现值、观测值和估计量。设输入W的不确定度以概率密度表示,V=1表示有雨,V=0表示无雨。以U表示所有确定性输入,以Y表示状态变量,并假定H过程是马尔可夫过程。在时刻t,已知量为预报变量的前期过程h0、状态变量y、输入变量u、v。设模型响应为s=γ(u,v),为模型输入的条件概率密度函数[3,10-13]。

式中,Φ为水文不确定度,即h的后验密度,定义为:

3 贝叶斯在水文不确定性分析中应用前景
贝叶斯理论在水文不确定性分析中,已经取得一定的进展,主要是应用方面。未来在理论方面可以进一步研究的方向主要包括以下:
(1)先验分布的确定,特别是一些无信息的先验分布问题。
(2)贝叶斯分析的稳健性问题。
(3)似然函数的选择问题。
(4)后验密度函数的随机抽样算法问题。
在应用方面,可以进一步拓宽其应用的领域。并和反映水文系统特性的灰色理论、模糊理论、随机理论有机结合。可以将先验分布考虑成灰色先验分布,似然函数表示成模糊似然函数,耦合这些表示水文不确定性的方法,实现对水文系统更深层次的认识。
[1]吴伯贤.贝叶斯方法在洪水频率分析中的应用[J].成都科技大学学报,1990,(49):69-75.
[2]戴荣.贝叶斯模型平均法在水文模型综合中的应用研究[D].南京:河海大学,2008.
[3]邢贞相.确定性水文模型的贝叶斯概率预报方法研究[D].南京:河海大学,2007.
[4]黄伟军,丁晶.水文水资源系统贝叶斯分析现状与前景[J].水科学进展,19945,(3):242-247.
[5]梁忠民,戴荣.基于MCMC的水文模型参数不确定性及其对预报的影响分析[C].南京:中国水利水电出版社,2008.
[6]R K.Bayesian system for probabilistic river stage forecasting[J].Journal of Hydrology.2002,268(1-4):16-40.
[7]RK,JMC.Hydrologicuncertaintyprocessorforprobabilisticstagetransitionforecasting[J].JournalofHydrology.2004,293(1-4).
[8]黄伟军,赵永龙,丁晶.径流的最优组合预测及其贝叶斯分析[J].成都科技大学学报,1996,(94):97-102.
[9]张铭,李承军,张勇传.贝叶斯概率水文预报系统在中长期径流预报中的应用[J].水科学进展,2009,20(1):40-44.
[10]王善序.贝叶斯概率水文预报简介[J].水文,2001,21(5):33-34.
[11]钱名开,徐时进,王善序等.淮河息县站流量概率预报模型研究[J].水文,2004,24(2):23-25.
[12]鄢来标,康玲.河道洪水概率预报方法研究[J].水力发电,2008,34(12):40-41.
[13]张洪刚,郭生练,刘攀.基于贝叶斯方法的实时洪水校正模型[J].武汉大学学报(工学版).2005,38(1):58-43.
Abstract:The basic principles of Bayesian analysis was introduced in this paper.Then the application of Bayesian analysis in hydrologic uncertainty was illustrated,including the application to watershed hydrologic forecasting,the application to river flood forecasting,the application to combined hydrologic forecasting,and the application to regionalization flood frequency analysis,etc.Finally,the prospect of the application of Bayesian analysis in hydrologic uncertainty was presented.
Key words:Bayesian analysis;uncertainty;parameter
责任编辑:宏彬
APPLICATIONS OF BAYESIAN THEOREM FOR HYDROLOGICAL UNCERTAINTY ANALYSIS
ZHOU PingZHU Ren-yi
(Physics Department of Chaohu College,Chaohu Anhui 238000)
O212.8
A
1672-2868(2010)03-0023-05
2010-03-06
周平(1982-),女,安徽巢湖人。巢湖学院物理与电子科学系教师,硕士。

