构建新升本院校数学与应用数学专业（师范）基于分类培养的分层教学模式

赵开斌钱云张千祥

（巢湖学院数学系，安徽巢湖238000）

构建新升本院校数学与应用数学专业（师范）基于分类培养的分层教学模式

赵开斌钱云张千祥

（巢湖学院数学系，安徽巢湖238000）

针对新升本院校数学与应用数学专业（师范）学生实际情况，探索基于分类培养的分层教学模式并进行实践，取得良好效果。

新升本院校；培养目标；分层教学模式

1 现状与背景分析

随着高校扩招，最近几年我国新升了一批本科院校，这批院校承担了扩招的主要任务，为我国高校的跨越式发展作出了巨大贡献，同时也派生出一系列新问题。

新升本院校数学与应用数学专业（师范）所招的学生，相当来说，数学基础不是太好。学生第一志愿报考的为数较少，绝大多数新生迫于高考严峻形势，填报志愿时填写专业服从，数学学习态度与意愿千差万别。数学学科较其他学科，有其自身特点：理论性较强，知识累积性强，知识呈一环扣一环的螺旋式递进结构，对数学思维有较高要求。学生入校后稍有懈怠，开始环节没能学好，严重影响后期的学习，尽管大多数学生录取时，高考分数差不多，但在大学学过一年半载以后，差距逐步显现，随着时间推移表现愈发明显。如有的学生一、二年级数学分析、高等代数没学好，后期课程的学习非常困难，或本身数学思维欠缺，也将严重影响数学的学习，典型表现为考试时不及格面过大，本课题组就考试就不及格面过大问题，进行了深入探讨。我系06级《概率论》课程以班级为单位的学生成绩呈双正态分布，而不是正态分布，表明同一班级学生中有一群体学习态度有问题，或学习上有障碍。尽管现各高校基本上实习重修制，但如对这一群体学生不予以特别关注，不进行有针对性的帮助，学习态度有问题的重修时仍存在问题，学习有障碍的重修时仍有障碍。

针对以上问题，本课题组提出并在我系实行新升本院校数学与应用数学专业（师范）分类培养分层教学的模式。

新升本院校数学与应用数学专业（师范）的培养目标大体上应有三类培养方向。

第一类方向为以后从事数学教育方向的（教师，主要是中学教师）；第二类方向为以后从事数学科学研究（考研的）；第三类为以后从事数学实际应用方向的人才。针对上述培养目标及学分制的要求，在三、四年级选修课程方面设置不同的模块，指导学生们根据自己今后发展方向选择自己的选修课模块，但在一、二年级的必修课程，也应充分考虑学生的差异性，进行分层教学。

对于第一类过去非常重视，今后仍需重视，为社会培养输送优秀的中学数学教师是师范院校的已任。对于第二类（考研的）这几年研究生招生扩招，这部分比重逐年增加，考研应该是学生自身的选择，专业培养上本不应该为其特别关注，但考虑到这一群体对改善学风，提高就业有显著贡献；也需要重视，特别强调对第三类方向的高度重视，大力加强数学实际能力的培养。新升本院校大都属应用型学校，培养应用型人才，应用型人才的显著特点是注重知识的有效管理与应用。而不是进行知识的发现与挖掘，也就是说数学与应用数学专业的学生既要注重学数学，更要注重用数学。过去数学与应用数学专业学生除了要求学习数学与应用数学的基本理论和基本方法，还要求接受严格的数学思维训练，属精英培养模式，现在这样“一刀切”的要求未免“削足适履”，脱离大众教育现实，上述三类培养方向，除第二类仍需要求严格的数学思维训练，一，三类主要是学习数学与应用数学的基本理论和基本方法。

确立了三类培养目标，围绕三类培养目标，本项目组提出应实行分层教学模式。分层教学模式是教师根据学生的学习基础，接受能力和学习需求，制定出不同的教学目标和内容，提出不同的教学要求，采取不同的教学方式进行教学，从而最大限度的调动每一个学生的学习积极性，让不同层次的学生都能保证充分发展的一种教学模式。分层教学的构想来源于当代多种先进教学思想的融合，包括个体差异与因材施教理论，布鲁姆的掌握学习理论，维果茨基的“最近发展区”理论以及巴班斯基的“教学过程最优化理论”。其精髓是因材施教。因材施教原则在我国早就被广泛关注，我国古代教育家、思想家孔子曾提出“中人以上，可以语上也，中人以下，不可以语上也”即教学要“因材施教，因人而异”。因材施教原则要求教师教学时要从学生实际出发，教学目标、教学内容、教学方法要适合学生的认知水平，考虑学生的个性特点和个性差异让每个学生都能在各自原有的基础上得到充分发展，真正做到“为了一切学生”。

我国中学教育中很多学校都在探索分层教学，高校开展的较晚，目前公共课程大学英语，高等数学也有探索，大都是停留在分班授课层次[2][3]。个别课程也在进行分层教学尝试[4]。整个专业进行分层教学的尝试，目前未见（就本课题组所知是如此）。

2 分层教学模式的实践与探索

分层教学的实施是以教学大纲为准绳，根据数学与应用数学专业的知识结构和学生的认识能力，发展方向合理的确定各层次学生的教学要求，改变过去“一刀切”的做法。力求准确的把握各类学生的认知“最近发展区域”，在一、二年级的数学分析，高等代数等数学基础课核心课程教学中，强调基本理论，基本方法的掌握，对一部分学有余力数学基础较好的学生进行严格数学思维的训练。既不降低大纲要求，更不能使学生消化不良丧失信心，当然这里的基本理论基本方法有个界定问题，何为基本理论基本方法，本课题组认为，基本理论基本方法是今后学习必不可缺的理论和方法，是可持续性学习必不可少的理论和方法。对学困生采取低起点，先慢后快，由浅入深，循序渐近的方法。将基础训练目标分解成有梯度的连贯的几个分目标。允许学困生根据自己的实际情况，一步或几步逐步的达到大纲要求。对没有考研打算，又不想从事教师职业的学生，应大力加强数学应用能力的培养，倡导用数学、做数学，加强数学实验、数学建模、数学软件、计算机编程课程的教学，为以后从事数学实际应用工作打下扎实基础。对学优生（今后考研的）则强调数学思想的启迪，数学知识的挖掘、数学思维的严格训练以便这部分同学今后的继续深造。对三、四年级学生根据其自身成绩、兴趣、发展方向，学业导师为其选课提供参考。

2.1 数学核心课程三个层次的分层教学模式

因材施教，关注学生的个性发展，满足学生不同层次的要求。教师首先深入了解学生的情况，我国高校生师比较高，教师要全面了解学生情况有点勉为其难，本项目组设想设计一些科学的测评方案供学生准确为自己定位，对自己成绩、兴趣、发展方向界定提供依据和参考。

在一年级、二年级、三年级的数学核心课程中，分为Ⅰ，Ⅱ，Ⅲ三个层次进行数学，比例大约为30%，30%和40%，分层的依据有三条：

①一是学生的数学基础与素养（通过测试题测试）

②二是结合学生毕业后的意向（对应三类培养目标）

③三是学生的学习意愿

各教学层次在知识的系统掌握方面目标是相同的，就是在有限的时间内让每个学生掌握基本的数学知识。但针对每个层次学生的特点确定不同的教学目标和要求。目标的制定以“跳一跳够得着”为标准，既不要因为目标过高而使学生丧失学习兴趣，又不要因目标过低而使学生的潜能挖掘不出来。

对于层次Ⅰ的学生（以后发展方向为考研，从事数学研究、高校教师工作），由于学生的数学基础与素养较好，学习态度端正。在完成大纲规定的基本数学知识基础上，对相关知识进行拓宽加深，课堂教学中可适当开展研究性学习，培养学生的创造能力和创造意识，突出学生在教学中的主体地位。学生的数学知识获得不完全是通过教师传授而是学生在一定背景和环境下，利用必要的学习资源，通过师生之间的交流，及学生的有效学习主动获得。教师的主导作用体现在：提供资源、创设情景，引导学生主动参与、自主进行问题探索学习；设置活跃创造性智能的环境条件，实施激疑顿悟的启发教育，让学生有意识地遵循和利用创造性思维方法，来突破常规、放开思想、寻找复杂消息、有效解决复杂问题。教学内容上，注重数学理论的挖掘，设计一些难易适中的问题让学生进行思考、研讨，鼓励学生自己查阅相关文献，撰写小论文，不断提高学生创新意识和创新能力。

承担层次Ⅰ教学任务的老师有一定的科研背景和科研能力。

对于层次Ⅱ学生（面向培养中学教师），系统地、严谨地传授大纲规定的数学基础知识，比较难的证明过程和理论略述。使学生熟练地掌握相应地数学思想、数学思维，不过分注重理论深度。但应拓宽知识点的背景，来龙去脉，透彻地介绍一些相应地数学史，注重知识点与中学数学的联系。从历史的角度探讨数学知识的产生发展过程，学习数学家思考问题和解决问题的方法。除了数学知识、解题能力以外，重要是培养学生数学观念，即让学生学会进行数学的思考，用数学思想知方法处理问题，用数学精神感知人文精神，这对以后从事初等教学教育是非常重要的。课堂教学设计的问题相对要简单些、梯度小一点，采用“小步子、慢速度”的教学原则，课堂教学采取精讲多练、循序渐进、布置作业也多以模仿性、基础性为主，加强课后辅导工作，承担这一层的教学的教师做到教学认真、严谨、耐心，最好有教过中学教学经验的老师。

对于层次Ⅲ学生（以后从事数学应用工作），在完成教学大纲规定内容的基础上，着重培养学生利用数学知识解决实际问题的能力，教学方式注重案例教学、讲授知识点，尽量联系社会生活中实例，通过分析、假设、数学化建立相应数学模型，教学过程中穿插一些数学实验演示，利用数学软件解决实际问题的实例。对数学理论要求放低些，弱化理论证明，让学生了解相应理论背景、作用以及应用过程。结合教学内容，突出数学建模思想，教会学生如何用数学语言描述实际问题，如何用数学工具来解决实际问题，让学生深切地感受到他们现在所学的那些看来枯燥无味但又似乎是天经地义的概念、定理和公式，并非无本之末、无源之水，也不是人们头脑中所固有的，而是有其现实的来源与背景，正如严士健先生指出的：“教材应结合日常生活及其他领域中的问题，举出更好地例子，以便学生体验数学教学与生活的关系，训练学生应用数学分析问题解决问题的能力，更主要的是让学生具有应用数学的意识，真正认为数学有用，知道哪些生活、学习或生产问题可以用数学来解决。“学数学”是为了“用数学”，“教数学”是为了让学生理解“数学思想”。从事这一层次基础课教学的老师有从事数学建模活动的经历，善于创造实际问题的情景，让学生解决一些简单的实际问题，并强调将数学结果同实际语言表达出来。

对于（Ⅱ），（Ⅲ）两层次的学生，尽管降低了数学理论要求，但学生在学习过程中可能还会有障碍。教师应有目的鼓励并引导学生学习，提高学生的学习兴趣，善于抓住学生学习的积极因素，利用一切机会让学生参与教学活动，大胆设疑、大胆探索、大胆提问，借以激发学生的学习兴趣。更重要的是教师还要适当地、不失时机地给学生鼓励和表扬，以强化学生的自我效能感。从心理学角度看，随着自我效能感的增强，学生自我表现愿望得以满足，他们的学习兴趣也就会愈加浓厚。

2.2 分层教学的考核方式

分层教学必然涉及到分班，因而必涉及考试问题与成绩评定问题。由于一份试卷不能同时兼顾多钟层次不同教学要求，理论上讲应当分开考试，才能较好地衡量学生的学习效果。但分开考试难免出现高层次班级学生低于低层次班级学生的分数的情况。对于学生，分数问题是一个敏感的问题，往往涉及评优、奖学金等切身利益，如处理不当，分层教学很难实施。

成绩评定是教学中的重要环节，直接反映学生的学习情况，同时也反映教师的教学效果。因此分层教学必须处理好学生的成绩评定问题，结合学年学分制，分层教学应更关注教学过程，成绩评定实行平时考核成绩+期末考试成绩的综合模式，赋予平时成绩以更大的权重。平时考核的内容与形式根据不同层次的学生的实际情况和教学目标，由授课教师自行确定。如对（Ⅰ）层次学生，平常考核以单元测验、课程论文与研讨的方式为主，对（Ⅱ），（Ⅲ）层次学生，平常考核的习题课练习、习题课提问和数学试验操作为主，辅以作业、笔记检查（以督促学生学习）。而期末考试各层次学生采用统一命题、统一阅卷、闭卷考试，以保证分层教学中各层次学生都必须达到教学大纲规定的要求。命题时必须熟练课程教学的基本要求，提高试题的信度和效度，在保证教学基本要求的前提下适当降低灵活性和提高性，基本题目的分值应保证在70分上下，保证基础较差、稍作努力的学生能够及格；同时考试题目可以出部分提高性、综合性的题目。但这些题目的分值要控制在20分以内，也可以在试题中增加附加题。每个学生可以根据自己的水平决定做或不做；还可以组织有关的学科竞赛：如（Ⅰ）层次采用数学竞赛；（Ⅱ）层次采用教学基本功竞赛；（Ⅲ）层次采用数模竞赛，将课程综合性、提高性的内容以这种方式考虑进来，在有关评奖评优活动中适当参考学科竞赛的成绩。总之，在成绩评定方面，在不违背教育教学规定的前提下进行一定的创新，克服分层教学中成绩评定的障碍。

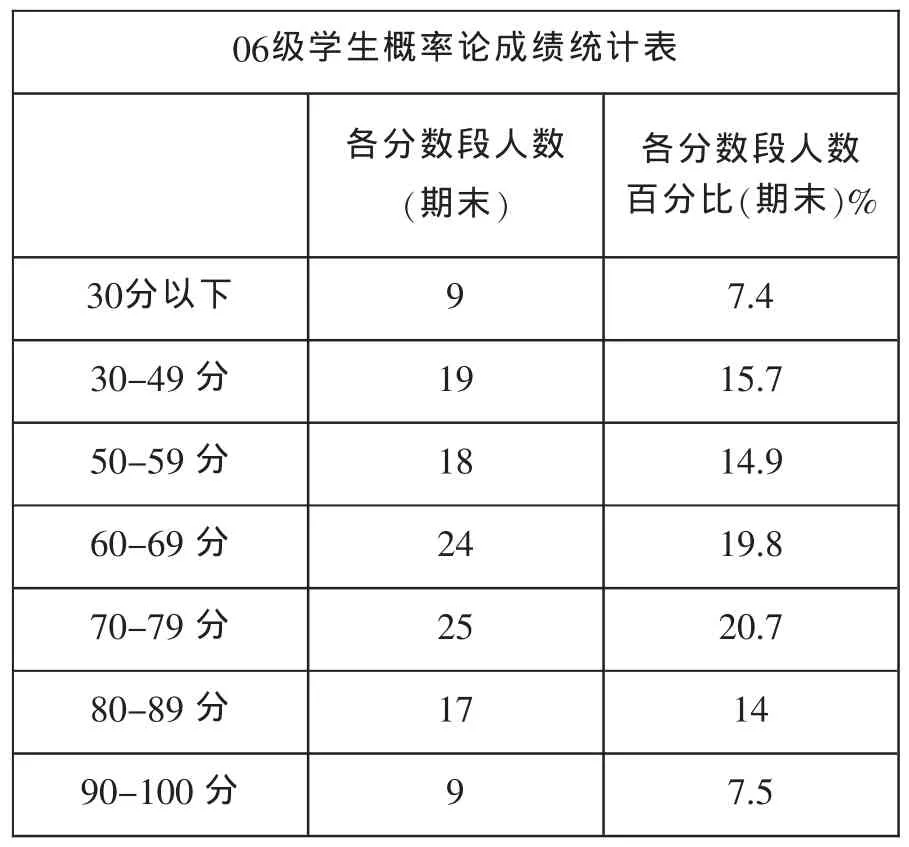
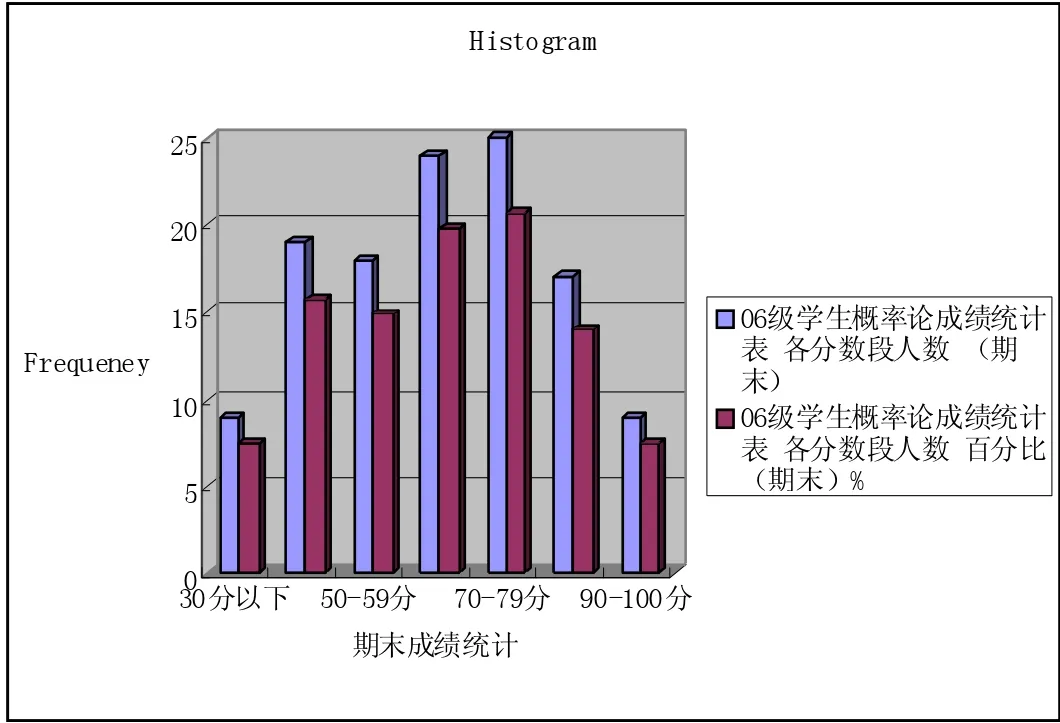
06级学生概率论成绩统计表各分数段人数各分数段人数（期末）百分比（期末）% 9 7.4 1915.7 1814.9 2419.8 2520.7 1714 9 7.5

3 分层教学实施产生的效果

分层的教学改革是对现代教育理念下学分制的完善与补充，是在现有教学软、硬件资源相对不足情况下与学分制的有机结合，是使每个学生都得到激励，提高学生学习数学的积极性，促进包括基础较差学生在内的所有学生发展的有效措施。通过我系一、二年级两年来的分层教学实践，学生的学习兴趣得到了提高，学生自主学习的能力得到了增强，不同层次学生学习的有效性和目的性得到了充分体现。表现在我系准备考研同学人数明显增加，报名参加大学生数学建模竞赛的人数也增加了很多。很多同学的教育教学技能得到了加强（报名参赛的同学也很踊跃）。更为明显的是各门课程的平均成绩和及格率也得到了稳定的提高。

下面是我系06级学生和08级概论论成绩的比较：

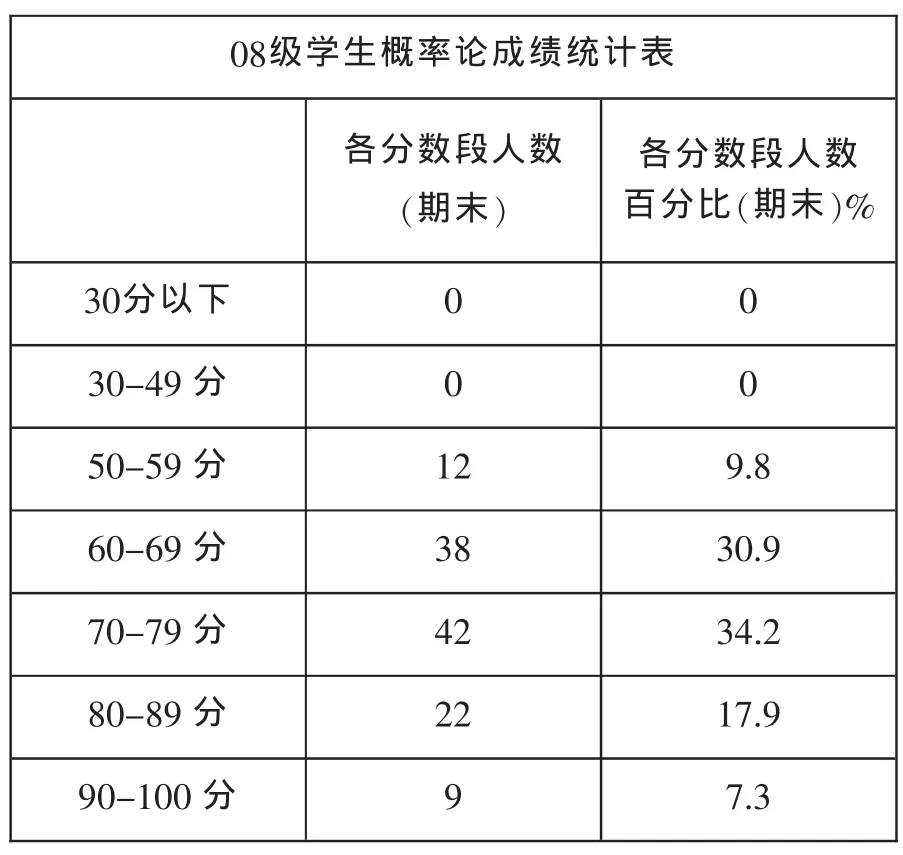
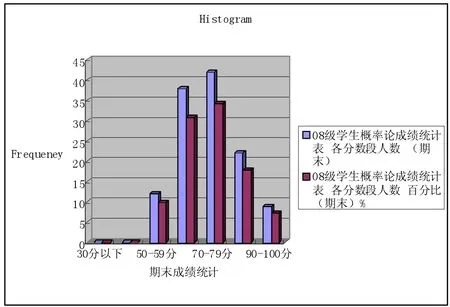
08级学生概率论成绩统计表各分数段人数（期末）各分数段人数百分比（期末）% 30分以下00 30-49分00 50-59分129.8 60-69分3830.9 70-79分4234.2 80-89分2217.9 90-100分97.3

结论

分层教学作为一种教学组织形式，其实施具有一定现实背景和理论支撑，结合我系学生的培养目标及实际情况，分为三个层次实施教学。通过二年多的实践，取得了一定的成就。今后我们将进一步遵循认识论和教学规律，持之以恒地实践。从实际情况出发，不断总结经验教训，力争取得更为显著的效果。

[1]柯力，王华，方向明.对构建大学个性化教学体系的思考[J].中国高等研究，2004，（10）.

[2]朱石焕；康会光.高等数学分层教学的改革与实践[J].中国科技创新导刊，2008，（17）.

[3]师尚贵，李士明.高等师范院校公共课分层教学的理论研究[J].大庆师范学院高报，2006，（3）.

[4]段宝彬等.常微分方程课程分层教学的探索与实践[J].大学数学，2009，（6）.

责任编辑：陈凤

G642

A

1672－2868（2010）03－0126－05

2010－02－26

本文受安徽省高等学校省级教学研究项目资助（项目编号：2008jyxm438）。

赵开斌（1965－），男，安徽无为县人。副教授。