InAs/InxGa1－xSb 二类超晶格红外探测器的吸收波长与电子-空穴波函数交叠的研究*

黄建亮 卫炀 马文全杨涛 陈良惠

(中科院半导体研究所纳米光电实验室，北京100083)

(2009年7月21日收到;2009年9月3日收到修改稿)

InAs/InxGa1－xSb 二类超晶格红外探测器的吸收波长与电子-空穴波函数交叠的研究*

黄建亮 卫炀 马文全†杨涛 陈良惠

(中科院半导体研究所纳米光电实验室，北京100083)

(2009年7月21日收到;2009年9月3日收到修改稿)

运用包络函数模型和传输矩阵方法计算了二类超晶格的能级结构.考虑到InAs与InxGa1－xSb结合存在应变，在计算中InAs/InxGa1－xSb二类超晶格的带阶采用模型固体理论处理.因为吸收系数与电子-空穴波函数交叠成正比，所以研究了InAs/InxGa1－xSb二类超晶格红外探测器的吸收波长和电子-空穴波函数交叠与InAs层厚度，InxGa1－xSb层厚度，In组分之间和周期数的关系.结果表明，吸收波长随InAs层厚度的增大而增大，随InxGa1－xSb层厚度增大而增大，随In组分增加而增大，随周期数的增大，先减小后不变.而电子-空穴波函数的交叠随InAs层厚度的增大而减小，随InxGa1－xSb层厚度增大也减小，随In组分增加而稍微增大，随周期数的增大，先增大后缓慢增加，然后基本上保持不变.另外，发现在相同的吸收波长下，InAs层的厚度与InxGa1－xSb层的厚度的比值越大，波函数的交叠也越大.

二类超晶格，红外探测器，波函数的交叠，传输矩阵

PACC:0670D，2940P

1. 引言

红外探测器在国家安全领域与民用领域有着非常重要的意义.红外探测器发展的趋势是更高的灵敏度，更高的工作温度以及更大的面阵规模［1—3］.制冷型红外探测器虽然有着更高的成本，但其极高的探测灵敏度也是非制冷型红外探测器所无法企及的，因此制冷型红外探测器在军事领域以及某些需要较高探测灵敏度的民用领域具有重要的应用.目前，就制冷型红外探测器而言，在3—5μm的中波波段，碲镉汞红外探测器已经非常成熟，而且碲镉汞红外探测器具有很高的量子效率、优异的探测性能和较高的工作温度.但是随着探测波长的增加，碲镉汞红外探测器的材料生长和器件工艺制作难度急剧增加，因此，碲镉汞红外探测器在8—12μm的长波波段受到一定的挑战，而且探测器成本极为昂贵，在波长大于14μm和约小于20μm的甚长波波段碲镉汞探测器则遇到巨大挑战.另一方面，起步于20世纪90年代量子阱红外探测器，虽然通过能带工程的方法和分子束外延以及金属有机气相化学沉积技术的日趋完美，量子阱红外探测器的探测波长可以覆盖从中波到甚长波波段，但是与碲镉汞红外探测器相比，量子阱红外探测器具有更低的量子效率，更低的探测灵敏度以及更低的工作温度.

最近几年，InAs/InxGa1－xSb二类超晶格材料日益受到重视，因为InAs/InxGa1－xSb二类超晶格中的InAs的导带底比InxGa1－xSb的价带顶还要低，从而电子和空穴空间分离，俄歇复合率大大减小，载流子寿命较长［4］.而且在长波及甚长波波段，InAs/ InxGa1－xSb二类超晶格对俄歇复合的抑制作用也较明显［5］.因为以上特性，InAs/InxGa1－xSb二类超晶格材料引起了广泛的注意，其在长波及甚长波波段红外探测器中的应用及优势是不言而喻的.根据最近的一些报道，基于InAs/GaSb二类超晶格的中波红外探测器工作温度可以达到240K［6，7］和300K［7］，并且具有很高的探测率，240K的探测率可达2×109cm(Hz)1/2/W.另外，InAs/GaSb二类超晶格红外探测器的探测波长已经做到了长波［8］甚至甚长波的波段［9］.除载流子寿命因素外，探测率还与量子效率相关［10］，而量子效率与吸收系数成指数关系，吸收系数又正比于波函数的交叠［11］.所以在InAs/InxGa1－xSb二类超晶格红外探测器的优化设计中，除探测波长，还应考虑波函数的交叠.

本文给出了计算InAs/InxGa1－xSb结构的分立能级和电子-空穴波函数交叠的理论模型.模型基于包络函数方法，传输矩阵方法以及要计算的探测波长处于红外波段的假定，考虑了InAs/InxGa1－xSb材料之间存在应变，引入了模型固体理论来处理带阶.假定计算的探测波长处于红外波段，这样可以避免在边界处的InAs的电子包络波函数与InxGa1－xSb的空穴包络波函数相衔接，电子和空穴的有效质量不受影响，直接运用查找的有效质量来计算.此理论模型计算出的InAs/InxGa1－xSb的吸收波长和波函数交叠的趋势与目前报道的一些实验符合很好.

2. 理论

InAs/InxGa1－xSb超晶格的异质结能带结构如图1所示，能带结构为二类超晶格的能带结构.由于能带为二类结构以及界面之间存在应变导致能带结构发生变化，不能直接运用导带与价带的带阶比值来计算带阶，从而运用模型固体理论［12］来计算带阶.由于缺少InAs及InxGa1－xSb的平均价带能量Eav随温度的变化参数，所以引入ΔΕ=0.1 eV，其意义为InAs的导带底能级与InxGa1－xSb价带顶能级的差，这一数值是目前被广泛接受的，且与In组分无关［13］.如图1所示.通过模型固体理论计算得出导带的变化，价带变化以及重空穴的受到应变之后的变化.得出考虑应变之后的带阶为

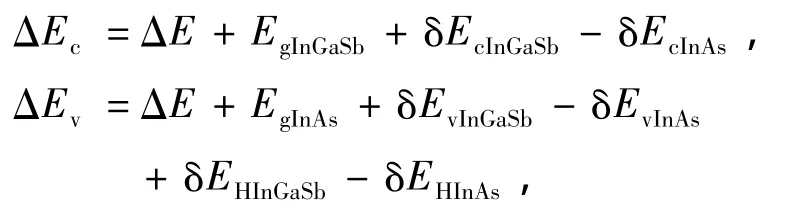
其中ΔΕc，ΔEv分别为导带的带阶和价带重空穴的带阶;EgInGaSb，EgInAs为InxGa1－xSb和InAs的带隙; δEcInGaSb，δEcInAs，δEvInGaSb，δEvInAs分别为InxGa1－xSb和InAs受到应变后，导带和价带发生的变化量; ΔEHInGaSb，ΔEHInAs为InxGa1－xSb和InAs受到应变之后重空穴能级进一步发生分裂量.这些参数都可以通过模型固体理论来求解(参考附录)，InxGa1－xSb和InAs的基本参数来源于文献［14］.

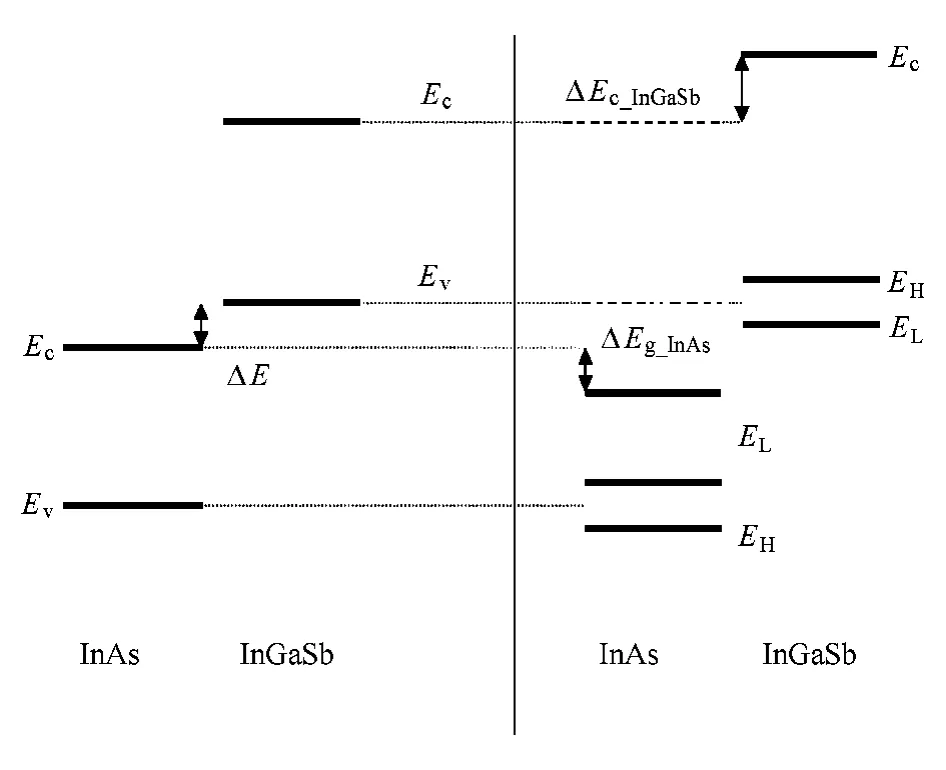
图1 InAs/InGaSb能带结构图，左边为InAs-InGaSb未生长在一起时的能带结构图，右边为InAs-InGaSb生长在一起形成二类超晶格时的能带图

得出带阶之后，运用传输矩阵方法［15］求解超晶格的能带结构，从而得出电子和重空穴的一系列分立能级，对于红外探测器而言，电子基态E0与空穴基态能量EH0之差即为吸收能量，但是此计算出的能级是相对于阱底(阱底能级为0 eV)的大小，所以能级差为

根据λ=1.24/δE，从而进一步得出吸收波长.

InAs/InxGa1－xSb二类超晶格红外探测器利用带间跃迁吸收，即超晶格材料吸收红外光后，电子从价带能级跃迁到导带能级，对于InAs/InxGa1－xSb二类超晶格结构，电子和空穴在空间上是分离的，但是吸收系数正比于电子和空穴波函数的交叠，即电子和空穴波函数的交叠越大，吸收系数就越大，因而量子效率就越大，红外探测器的探测率就越大，这对于探测器而言就越有利.因此，在二类超晶格红外探测器的设计中，考虑电子和空穴波函数的交叠是必须的，并且具有非常重要的意义.所以本文中，电子和空穴波函数的交叠这个重要参数将被重点讨论.InAs/InxGa1－xSb的吸收系数可以写为［12］

其中u(c/n)为光场的平均能量密度，e0为光偏振方向的单位矢量，A0为光场强度，p为动量算符，ψi，ψf分别为跃迁的初始态波函数和末态波函数，Ei，Ef为初始状态和末状态的能级.方程(1)中的W(ω)∝∫ψi*ψfdz，说明吸收系数正比于波函数的交叠［11］.运用数值计算得出归一化的ψi和ψf，就可以计算出波函数的交叠.

3. 结果与讨论

根据上述的理论模型计算出InAs/InxGa1－xSb二类超晶格红外探测器的吸收波长和波函数的交叠与二类超晶格各个参数之间的关系.

3.1. InAs/InxGa1－xSb二类超晶格的能级与各参数之间的关系

图2(a)为计算的InAs/In0.23Ga0.77Sb在InAs厚度等于In0.23Ga0.77Sb厚度的情况下，能级与周期厚度的变化关系，其中横坐标为周期厚度的一半，在计算中超晶格周期数为10，作为例子，InxGa1－xSb材料中In组分x选用0.23.当InAs和InxGa1－xSb的厚度比较薄时，由于电子和空穴各自的波函数相互之间存在强的耦合，导致能级形成微带.可以看出随着周期厚度的增加，微带的宽度变得越来越窄，最后转变成为分立的能级，这是因为随着周期厚度的增加，电子和空穴各自的波函数相互之间的耦合变得越来越小.另外，随着周期厚度增加，超晶格的“带隙”即导带基态与价带基态能级间距减小，即超晶格材料变得越来越像金属.因此理论上，InAs/ In0.23Ga0.77Sb二类超晶格探测器的探测波长可以覆盖从约3μm到20μm甚长波段甚至更长的波段.

我们也计算了InAs与InxGa1－xSb层厚度的比例不为1∶1，能级与InAs或者是In0.23Ga0.77Sb厚度的关系，结果如图2(b)和(c)所示.在计算过程中，分别固定In0.23Ga0.77Sb或者是InAs厚度为20，再改变InAs或者是In0.23Ga0.77Sb厚度得出的能级.从图中可以看到，和图2(a)具有类似的趋势，微带随着厚度的增加越来越窄，最后为分立的能级.但是和图2(a)不同的是，图2(b)的导带微带里的值都在减小，而价带的微带里的值是向中间某个值收缩，同样图2(c)的导带微带里的值也是向中间某个值收缩.这可能是因为只改变InAs(或In0.23Ga0.77Sb)厚度，相互之间的耦合作用V减小，空穴(电子)单个量子阱的本征能量Ea不变，而能级又可写为Eq=Ea－2Vcos(qd)，从而显示出能级向Ea收缩现象［12］，这里的q为超晶格生长方向的波矢，d是周期厚度.

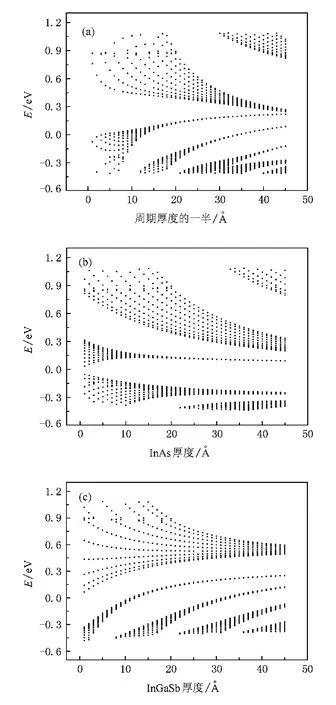
图2 (a)周期数为10，在InAs厚度等于In0.23Ga0.77Sb厚度情况下，能级E随周期厚度的变化，横坐标为周期厚度的一半; (b)周期数为10，在In0.23Ga0.77Sb厚度等于20情况下，能级E随InAs厚度的变化;(c)周期数为10，在InAs层厚度等于20情况下，能级E随In0.23Ga0.77Sb层厚度的变化

3.2. InAs/InxGa1－xSb二类超晶格的吸收波长与各参数之间的关系

图3(a)为超晶格周期数为10，在InAs和In0.23Ga0.77Sb厚度相等的情况下，吸收波长与周期厚度的变化.图中显示，随着周期厚度的变大，吸收波长在变大.由于InAs(或In0.23Ga0.77Sb)厚度的增大，E0和EH0减小，从而吸收跃迁的能量减小导致吸收波长增大.图3(b)分别为固定InAs或者是In0.23Ga0.77Sb厚度的变化，吸收波长随In0.23Ga0.77Sb厚度或者是InAs厚度的变化关系.同样可以看到随着厚度的增加，吸收波长在增加.但是InAs厚度对吸收波长的影响明显要大于In0.23Ga0.77Sb厚度对吸收波长的影响，由于电子主要是限制在InAs中，而空穴限制在InxGa1－xSb中，电子的质量远远小于重空穴的质量，因此相对于改变In0.23Ga0.77Sb厚度对空穴能级的影响，改变InAs厚度对电子能级影响比较大.图3 (c)展示了吸收波长与In组分的关系，随着In组分的增大，InxGa1－xSb的禁带Eg减小，从而使得导带帯阶ΔEc减小，电子基态能级减小，吸收波长增大.

3.3. InAs/InxGa1－xSb二类超晶格波函数的交叠与各参数之间的关系

由以上的计算可知，InAs/InxGa1－xSb的带隙可以覆盖从中波到甚长波甚至更远的范围，这意味着利用此“带间”跃迁的InAs/InxGa1－xSb二类超晶格红外探测器的探测波长可以覆盖从中波到甚长波甚至更远的范围.但是随着探测波长增大，由以上的计算可知InAs/InxGa1－xSb二类超晶格的周期变厚;对于二类超晶格结构，电子与空穴主要束缚在不同的材料中，即电子与空穴在空间是分离的;随着超晶格周期增大，电子波函数在InxGa1－xSb材料中的分布减小，而空穴波函数在InAs材料中的分布也减小，这导致电子与空穴波函数的交叠减小.吸收系数正比于波函数的交叠，因此研究波函数的交叠对于二类超晶格红外探测器的设计是非常重要的，这一点对于长波和甚长波红外探测器的设计更是非常关键.图4(a)显示了在不同周期厚度下波函数的交叠与周期数的关系图，可以看出随着周期数的增加，波函数的交叠先迅速的增大而后非常缓慢增加，当周期数大于10时，波函数的交叠变化就已经很小了，这意味着在红外探测器的设计中，周期数的设计一般大于10即可，更大的周期数并不能有效的增加吸收.波函数的交叠与周期厚度及In组分的变化关系在图4(b)中得以显示，图4(b)插图为对图4(b)的局部放大.可以看出，在相同的周期厚度时，In组分越高，波函数交叠越大.图4(c)中圆形曲线为，周期数为10，GaSb层厚度为20，只改变InAs层的厚度，其他参数不变得出波函数的交叠与InAs层厚度的变化关系图.方形曲线为，同样在周期数为10，InAs层厚度为20，其他参数不变得出波函数的交叠与GaSb层厚度的变化关系图.从图中可以看出，波函数的交叠随着InAs层或者是GaSb层厚度的增加而减小.

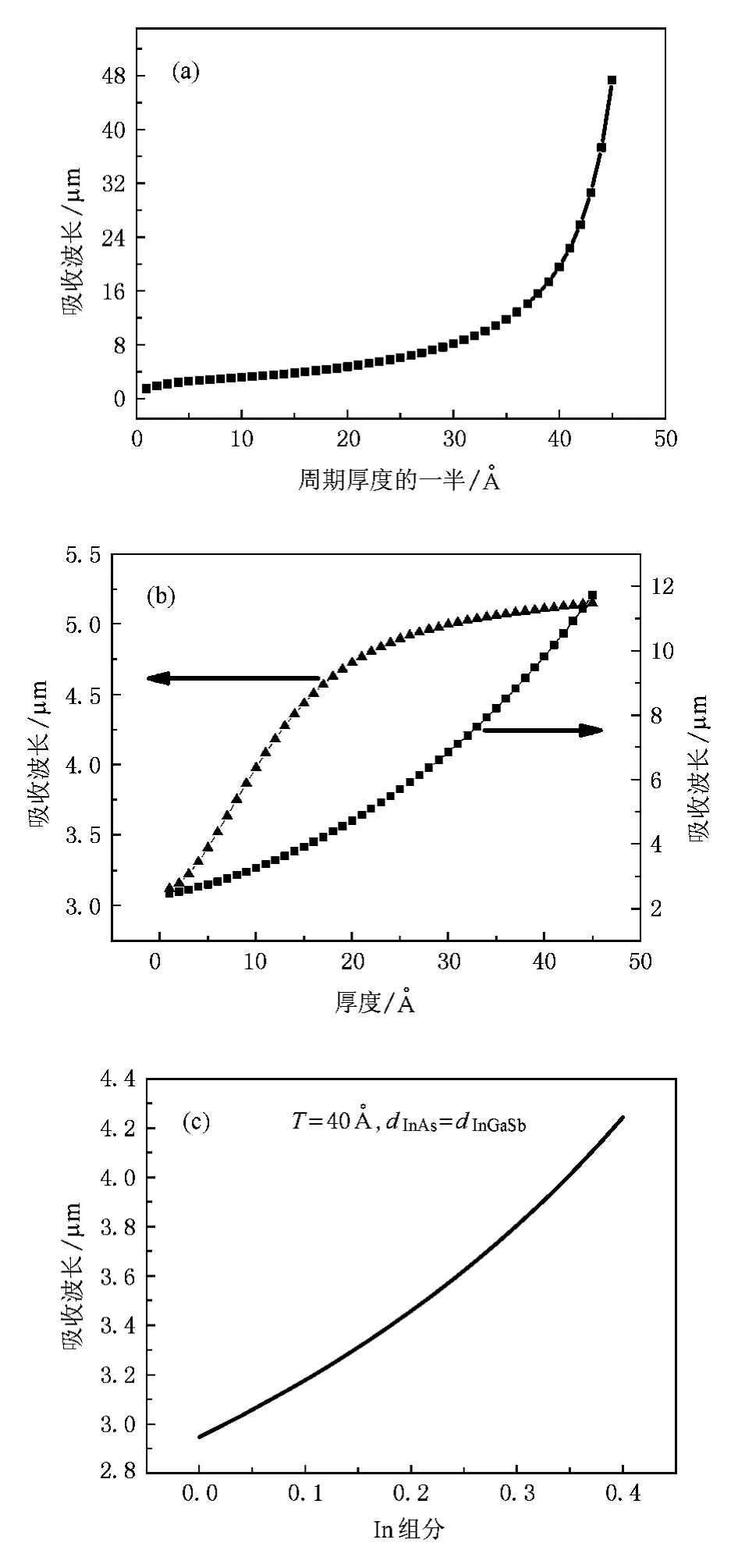
图3 (a)周期数为10，在InAs层厚度等于In0.23Ga0.77Sb层厚度情况下，吸收波长随周期厚度的增大而增大;(b)方形(■)曲线为周期数为10，在In0.23Ga0.77Sb层厚度等于20情况下，吸收波长随InAs层厚度的变化;三角形(▲)曲线为周期数为10，在InAs厚度等于20情况下，吸收波长随In0.23Ga0.77Sb层厚度的变化;(c)在InAs厚度和InxGa1－xSb厚度等于20情况下，周期数为10，吸收波长随In组分的增大而增大

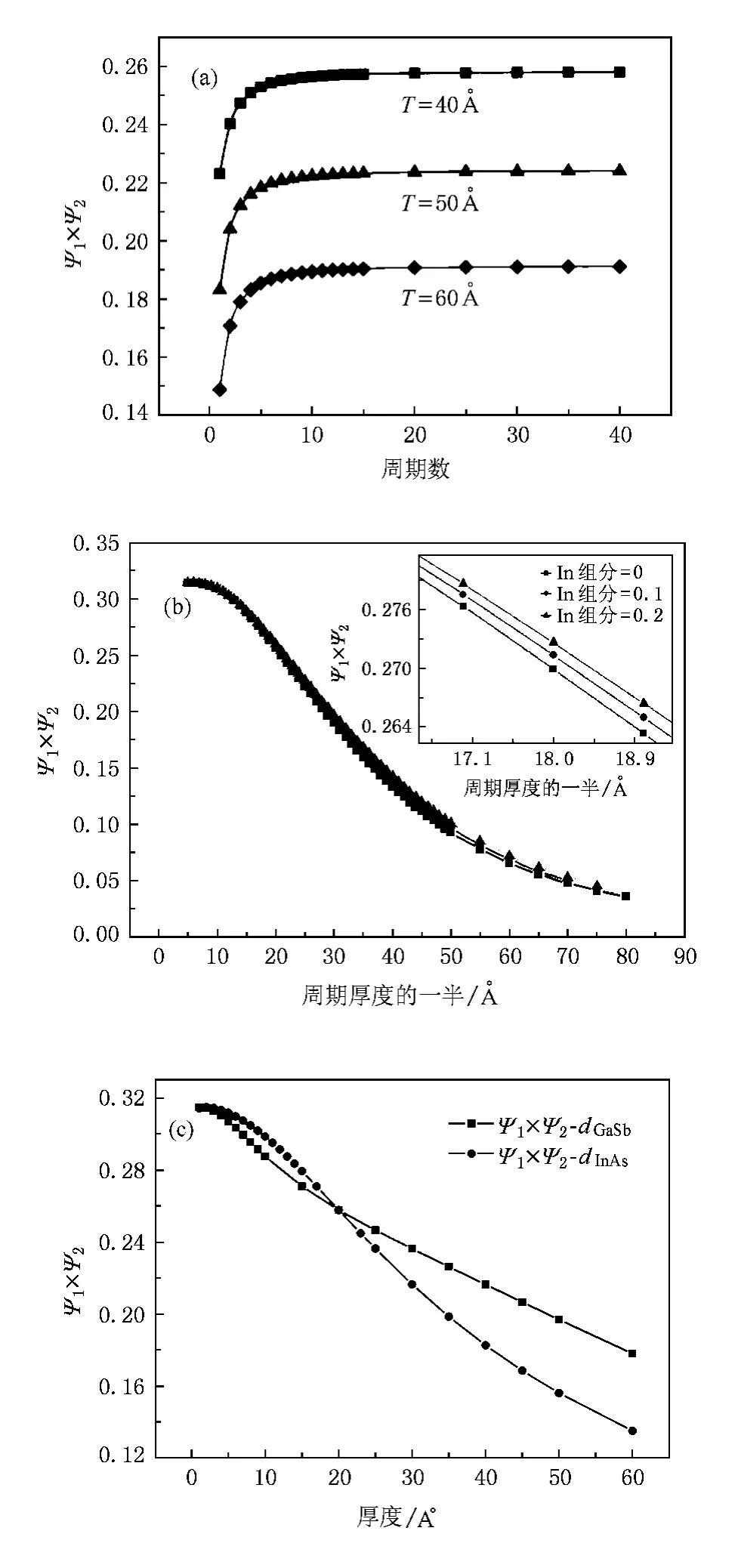
图4 (a)周期厚度分别为40(方形■)，50(三角形▲)，60(菱形◆)的InAs/GaSb，波函数交叠随周期数的变化，在周期数较小时，增大周期数，可以很快增加波函数的交叠，但是当周期数大于10，周期数的增大，波函数的交叠增加很缓慢，基本上保持不变;(b)InxGa1－xSb的In组分分别为0(■方形)，0.1(●圆形)，0.2(▲三角形)，周期数为10，InAs/InxGa1－xSb，波函数交叠随周期厚度的变化，随着周期厚度的增大，波函数交叠降低，插图为局部的放大，显示出In组分的增加，可以相应增大波函数的交叠;(c)圆形(●)曲线为:周期数为10，GaSb厚度为20的InAs/GaSb，波函数交叠随InAs厚度的变化，方形(■)曲线为:周期数为10，GaSb厚度为20的InAs/GaSb，波函数交叠随InAs厚度的变化

最后，作为例子，针对中波λ=4.0μm和甚长波λ=15.0μm的峰值探测波长，我们计算了利用InAs/GaSb，InAs/In0.15Ga0.85Sb，和InAs/In0.23Ga0.77Sb结构来实现这两个探测波长的情况.计算了InAs和GaSb，InAs和In0.15Ga0.85Sb，以及InAs和In0.23Ga0.77Sb的层厚比不同的情况，计算中超晶格周期数都为10.例如，对于层厚比为1∶1的情况，计算结果为:对于λ=4.0μm的探测波长，InAs/GaSb，InAs/In0.15Ga0.85Sb，和InAs/In0.23Ga0.77Sb超晶格结构的周期厚度应为54.4，40，和32.6，即每个周期中相应的InAs层厚度(或GaSb，In0.15Ga0.85Sb，In0.23Ga0.77Sb)应为27.2，20，和16.3.而对于λ =15.0μm的探测波长，InAs/GaSb，InAs/In0.15Ga0.85Sb，和InAs/In0.23Ga0.77Sb超晶格结构的厚度应为109.8，83.6，和75.2，即相应的InAs层厚度(或GaSb，In0.15Ga0.85Sb，In0.23Ga0.77Sb)应为54.9，42.8，和37.6.然而从波函数交叠的角度，这些结构的差别很大.图5是计算的采用以上提到的不同结构来实现中波λ=4.0μm和甚长波λ =15.0μm这两个探测波长波函数交叠的情况.可以看出，获得相同的探测波长，波函数的交叠随着InAs层厚度与In0.23Ga0.77Sb层厚度的比例增加而加强，并且随InxGa1－xSb材料的In组分增加而增加.从图3和图4，可以看出，InAs层厚度对探测波长影响较大，而InxGa1－xSb层厚度对探测波长影响相对较小，这是因为InAs层厚度的变化主要引起电子的能级变化，而InxGa1－xSb层厚度的变化则主要引起空穴能级的变化，电子的有效质量远小于空穴的有效质量，所以改变电子所在的阱宽(InAs厚度)对电子能级的影响远大于改变空穴所在的阱宽(InxGa1－xSb厚度)对空穴能级的影响，电子能级对于探测波长的影响占主导地位.但是InAs层厚度和InxGa1－xSb层厚度对波函数交叠的影响都较大.所以在具有相同探测波长情况下，增加InAs层厚度与InxGa1－xSb层厚度的比例可以减小器件的厚度，加强波函数的交叠，增强吸收系数，提高In组分也有助于减小材料的厚度，增加吸收系数.

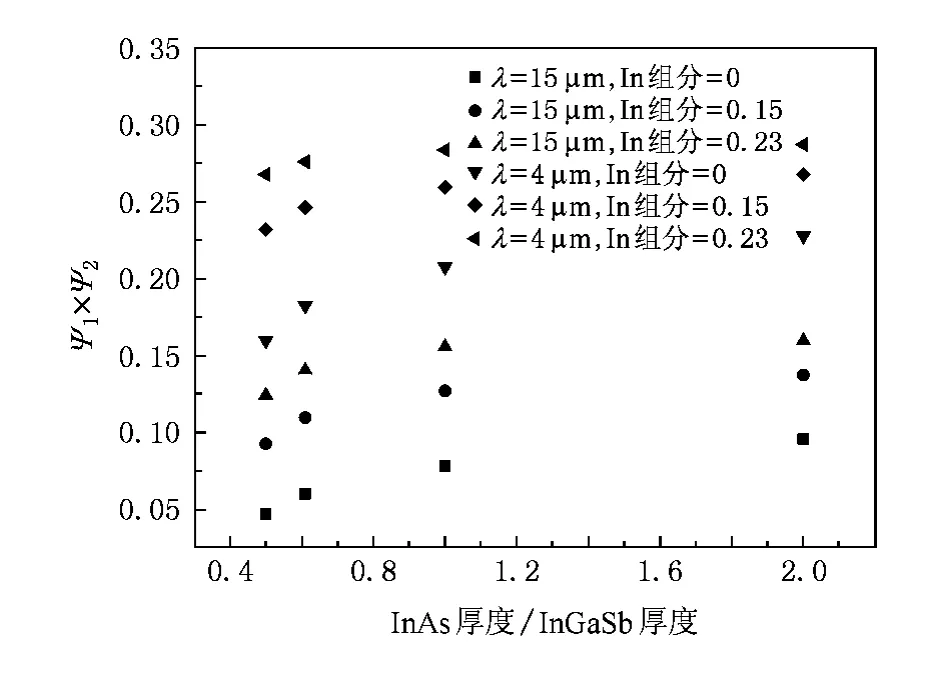
图5 吸收波长为4μm，15μm，周期数为10，In组分为0(倒三角，方形■)，0.15(菱形◆，圆形●)，0.23(侧三角，正三角▲)时，波函数交叠随InAs层与InxGa1－xSb厚度比值变化;增加In组分和增加InAs层与InxGa1－xSb层厚度比值有助于增大波函数的交叠

对于二类超晶格红外探测器的设计，以上数值计算结果指出了在保证探测波长实现的情况下如何增加波函数的交叠从而提高吸收系数的途径.但是具体的设计能否被采用，还应考虑高质量材料生长能否实现的问题，例如，InAs的晶格常数为6.0584，而InSb晶格常数为6.4794，两者的晶格失配为6.95%，而InAs与GaSb的晶格失配只有0.6%，因此，对于InAs/InxGa1－xSb二类超晶格，虽然计算表明提高In组分可以增加吸收，但设计的结构还应使得InxGa1－xSb的层厚在临界厚度以内.在能保证InAs层和InxGa1－xSb层材料处于临界厚度以内，从提高材料吸收的角度，InAs/InxGa1－xSb二类超晶格红外探测器的设计中，仍应尽量增加InAs层厚度与InxGa1－xSb层厚度的比例以及提高InxGa1－xSb层材料的In组分.

4. 结论

由于InAs/InxGa1－xSb结构的电子和空穴空间上的分离，所以设计一个InAs/InxGa1－xSb二类超晶格红外探测器要达到某个波长，不仅仅只考虑到这个波长值，而且需要考虑波函数交叠.本文运用包络函数模型和传输矩阵方法求解分立能级，吸收波长和波函数交叠.结果表明，在达到相同的波长，要提高吸收系数需减小周期厚度，增加周期数，增加In组分，提高InAs层厚度与InxGa1－xSb层厚度的比值.

附录模型固体理论计算InAs/ InxGa1－xSb的带阶

由于缺少关于InAs，InxGa1－xSb的平均价带能随温度变化的参数.所以引入了InAs导带底与InxGa1－xSb价带顶之间的间距ΔΕ=0.1 eV，来进行带阶的估算.

引入应变之后，在平行界面的方向上，它们的晶格常数应相等.它的表达式为［12］

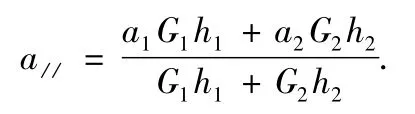
在垂直方向上晶格常数是不想等的，其表达式为［12］

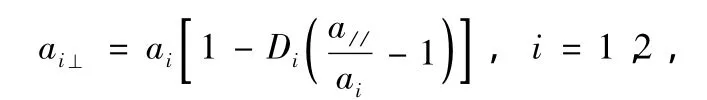
其中h是层厚，i表示不同的材料，Gi是切变模量，Di为应变模量都与弹性常量C11，C12，C44相关，对于(001)面，可写为［12］

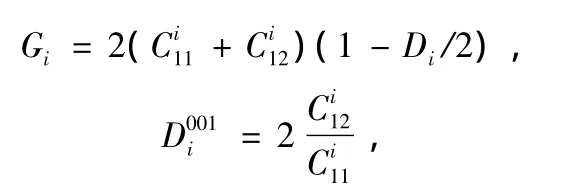
由于晶体在平行和垂直界面方向的应变，导致应变张量分量为

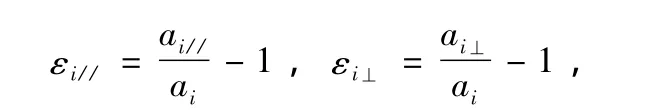
应变引起的体积变化和价带和导带的整体移动为［12］

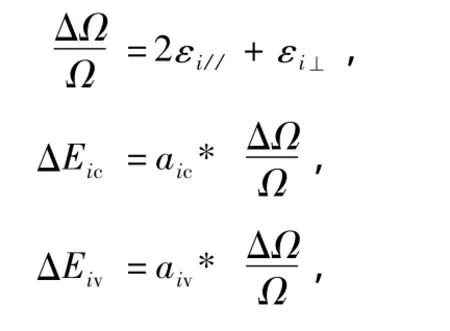
应变引起的另一变化是价带顶自旋轨道分裂后，使得重轻空穴进一步分裂，自旋轨道分裂带发生位移.其表达式为［12］

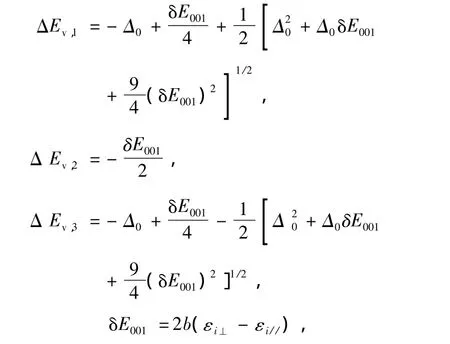
式中ΔEv，1，ΔEv，2，ΔEv，3为轻，重空穴和自旋轨道分裂带，b为价带边的形变势，Δ0为自旋轨道分裂能量［12］.

最后根据InAs/InxGa1－xSb能带图得出导带和价带的带阶表达式为

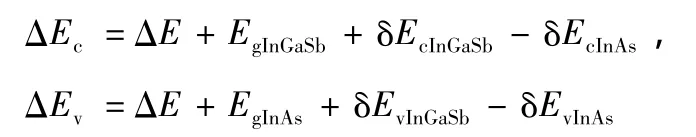
式中变量意义参考第二部分内容.

［1］Rogalski A 2007 Infrared Phys.Technol.50 240

［2］Becker L 2006 Proc.SPIE 6127 61270S

［3］Ashley T，Gordon N T 2004 Proc.SPIE 5359 89

［4］Youngdale E R，Meyer J R，Hoffman C A，Bartoli F J，Grein C H，Young P M，Ehrenreich H 1994 Appl.Phys.Lett.64 3160

［5］Grein C H，Yang P M，Platte M E，Ehrenreich H 1995 J.Appl. Phys.78 7143

［6］Plis E，Rodriguez J B，Kim H S，Bishop G，Sharma Y D，Dawson L R，Krishna S 2007 Appl.Phys.Lett.91 133512

［7］Li J V，Hill C J，Mumolo J，Gunapala S，Mou S，Chuang S L 2008 Appl.Phys.Lett.93 163505

［8］Delaunay P Y，Nguyen B M，Razeghi M 2009 Proc.SPIE 7298 72981

［9］Hoffman D，Nguyen B M，Huang E K，Delaunay P Y，Bogdanov S，PManukar P，Razeghi M，Nathan V 2009 Proc.SPIE 7222 722215

［10］SchneiderH，LiuHC2006QuantumWellInfrared Photodetectors(Germany:Springer)p11

［11］Chang Y C，Schulman J N 1985 Phys.Rev.B 31 2069

［12］Xia J B，Zhu B F 1995 Semiconductor Superlattice Physics (ShangHai:Science and technology Press)p388(in Chinese)［夏建白、朱邦芬1995半导体超晶格物理(中国上海:上海科学技术出版社)第388页］

［13］Smith D L，Maihiot C 1987 J.Appl.Phys.62 2545

［14］Vurgaftman I，Meyer J R，Ram-Mohan L R 2001 J.Appl.Phys. 89 5815

［15］Chuang S L 1995 Physics of Optoelectronic Devices(USA:John Wiley＆Sons.Inc.)p157

PACC:0670D，2940P

*Project supported by the National Basic Research Program(973)of China(Grant No.2010CB327602).

†Corresponding author.E-mail:wqma@semi.ac.cn

On detection wavelength and electron-hole wave function overlap of typeⅡInAs/InxGa1－xSb superlattice infrared photodetector﹡

Huang Jian-Liang Wei Yang Ma Wen-Quan†Yang Tao Chen Liang-Hui
(Laboratory of Nano-Optoelectronics，Institute of Semiconductors，Chinese Academy of Sciences，Beijing100083，China)
(Received 21 July 2009;revised manuscript received 3 September 2009)

In this paper，the detection wavelength and the electron-hole wave function overlap of InAs/InxGa1－xSb typeⅡsuperlattice photodetectors are numerically calculated by using the envelope function and the transfer matrix methods.The band offset is dealt with by employing the model solid theory，which already takes into account the lattice mismatch between InAs and InxGa1－xSb layers.Firstly，the detection wavelength and the wave function overlap are investigated in dependence on the InAs and InxGa1－xSb layer thicknesses，the In mole fraction，and the periodic number.The results indicate that the detection wavelength increases with increasing In mole fraction，InAs and InxGa1－xSb layer thicknesses，respectively.When increasing the periodic number，the detection wavelength first increases distinctly for small periodic numbers then increases very slightly for large period numbers.Secondly，the wave function overlap diminishes with increasing InAs and InxGa1－xSb layer thicknesses，while it enhances with increasing In mole fraction.The dependence of the wave function overlap on the periodic number shows the same trend as that of the detection wavelength on the periodic number.Moreover，for a constant detection wavelength，the wave function overlap becomes greater when the thickness ratio of the InAs over InxGa1－xSb is larger.

typeⅡsuperlattice，infrared photodetector，wave function overlap，transfer matrix method

book=212,ebook=212

*国家重点基础研究发展计划(973项目)(批准号:2010CB327602)资助的课题.

†通讯联系人.E-mail:wqma@semi.ac.cn