分数阶经验模态分解方法在机械故障诊断中应用

李志农,刘立州

(1.南昌航空大学无损检测技术教育部重点实验室,江西南昌330063; 2.郑州大学机械工程学院,河南郑州450001)

分数阶经验模态分解方法在机械故障诊断中应用

李志农1,2,刘立州2

(1.南昌航空大学无损检测技术教育部重点实验室,江西南昌330063; 2.郑州大学机械工程学院,河南郑州450001)

将经验模态分解方法(EMD)和分数阶Fourier变换基本理论相结合,提出一种基于分数阶Fourier变换的经验模态分解的机械故障诊断方法.仿真结果表明,提出的方法是有效的,尤其是对于用EMD分解方法无法进行有效分解的信号.如果时频平面旋转一定的角度,将信号从EMD难以分离的区域变换到可以用EMD分解有效识别的区域,然后经过EMD分解和分数阶Fourier反变换,就可以实现分量的提取.诊断实例进一步验证方法的有效性.

故障诊断;分数阶Fourier变换;经验模态分解;仿真

经验模态分解方法(EMD)是近年来兴起的一种新的信号处理方法.它基于信号的局部特征时间尺度,可以把信号分解成为若干个固有模态函数(IM F),而各个IM F分量突出了数据的局部特征.通过对其进行分析,可以更准确地把握原数据的特征信息,非常适用于非线性、非稳态过程.分数阶傅里叶变换(Fractional Fourier Transform,FRFT)作为傅里叶变换的一种广义形式,具有傅里叶变换所不具备的某些特点,能够对时变信号和非平稳信号进行有效的分析处理.FRFT可以理解为信号在时频平面内坐标轴绕原点逆时针旋转任意角度后,其构成的分数阶傅里叶域上的表示.从本质上讲,信号在分数阶傅里叶变换域上的表示,同时融合了信号在时域和频域的信息,是一种新的有效的时频分析方法.本文将经验模态分解方法与分数阶傅里叶变换理论相结合,提出了一种基于分数阶Fourier变换的经验模态分解方法,使原EMD无法分解的信号得以有效的分解.

1 经验模态分解方法

经验模态分解方法(EMD)是利用时间序列上、下包络的平均值确定“瞬时平衡位置”,进而把非平稳信号分解成一组稳态和线性的数据序列集,即固有模态函数.EMD方法分解信号是基于如下3条假定:(1)数据至少有两个极值,一个极大值和一个极小值;(2)特征时间尺度定义为相邻极值点之间的时间间隔;(3)如果数据没有极值点但有拐点,则可以通过对数据微分一次或多次求得极值,然后再通过积分来获得分解结果.这种方法的本质是通过数据的特征时间尺度来获得固有波动模式,然后分解数据;而上、下包络线的均值的确定是基于数据自身的局部特征的.因此,分解过程是自适应的.

EMD方法是通过一种被称为“筛分”处理的过程,来实现对信号进行分解的,有如下4个步骤[1-2]:

(1)确定数据序列x(t)所有的局部极大值点和局部极小值点,利用三次样条插值函数拟合形成原数据的上、下包络线;

(2)上包络线和下包络线的均值记作m1,求出h1=x(t)-m1.理想情况下,如果h1是一个IM F,h1就是x(t)的第1个IM F分量;

(3)如果h1不满足IM F的条件,则把h1作为原始数据,重复步骤(1),(2),可得到上、下包络线的平均值m11,然后再判断h1,1=h1-m1,1是否满足IM F的条件.如不满足,则重复循环k次,得到h1,k= h1,(k-1)-m1,k,使h1,k满足IM F的条件.记c1=h1,k.c1为信号x(t)的第1个满足IM F条件的分量,代表原数据序列中的高频部分.Huang等[3]将上述这样的处理过程形象地比喻为“筛选”过程.

(4)把c1从x(t)中分离出来,可得到r1=x(t)-c1.将r1作为原始数据重复步骤(1)～(3),可得到x(t)的第2个满足IM F条件的分量c2,重复循环n次,得到信号x(t)的n个满足IM F条件的分量.即可得到r2=r1-c2;…;rn=rn-1-cn.当rn成为一个单调函数不能再从中提取满足IM F条件的分量时,循环结束.由此可得到其中:rn称为残余函数,代表信号的平均趋势.

由此可以看出,经验模态分解方法对信号的每次分解都增加了一个细节(基本模态分量)和一个频率低于细节的低频分量,即第n次均值曲线,分解是对信号不断提取高频分量的过程.

2 分数阶Fourier变换

分数阶Fourier变换是一种将信号从时域变换到分数傅里叶域的方法,其定义[4-5]为

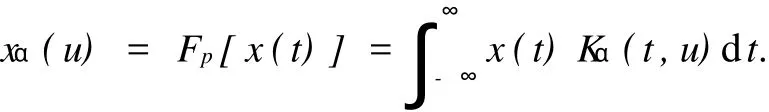
式中:α=pπ/2,p为分数阶傅里叶变换的阶数;Fp为分数阶傅里叶算子符号;Kα(t,u)为分数阶傅里叶变换的核函数,有

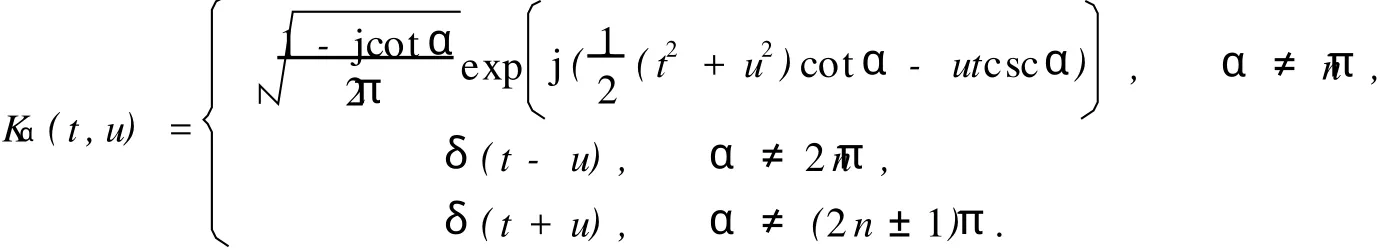
FRFT作为一种广义的Fourier变换,既与经典的Fourier变换有着天然的联系,又提供了经典的Fourier变换所不具有的性质.FRFT可看作是角度为α的时频面旋转变换,它提供了信号从时域到频域的全过程的综合描述.随着阶数从0连续增长到1,分数阶Fourier变换展示出信号从时域逐步变化到频域的所有变化特征.当阶数p取不同值时,故障信号的FRFT谱的能量集中性有优有劣.当选择恰当的阶数p时,就可得到能量集中性较好的分析图谱,从而能够更好地分析信号性质.另外,如果信号存在交叉项干扰或时间频率耦合问题时,也可通过在时频平面进行适当的旋转变换,以滤除交叉项干扰和解决时频耦合的问题.

至于最优阶数p的选择,文中采用步进选择的方法来实现.具体做法是:将阶数p在一定范围(0≤p≤2)按某个步长(比如0.1)进行步进尝试,以选取最优的p值.如果阶数p要求有较高的精确度,可以采用多次步进选择的方法来达到相应的精度要求.

3 仿真实验

对于有些信号,EMD分解方法无法有效分解.如果将时频平面旋转一定的角度,将信号从EMD难以分离的区域变换到可以用EMD分解有效识别的区域;然后,经过EMD分解和分数阶Fourier反变换,实现分量的提取.这样的旋转功能正是分数阶Fourier变换可以实现的.

这里,将分数阶EMD方法与Wigner分布相结合.在Wigner变换之前,先选择合适的分数阶Fourier变换阶数,在选定的分数阶Fourier变换域中进行EMD分解,得到一系列本征模函数,然后进行Wigner变换.这样就能有效消除交叉项干扰.

具体步骤如下:(1)观察时频分布并选取合适的角度,对信号进行分数阶Fourier变换;(2)对变换后的信号进行EMD分解,得到几个基本模态分量;(3)对每一个分量进行分数阶Fourier反变换;(4)对分数阶Fourier反变换后的每一个分量再作Wigner变换.

为了考察该方法的有效性,在此先进行仿真研究.仿真信号为

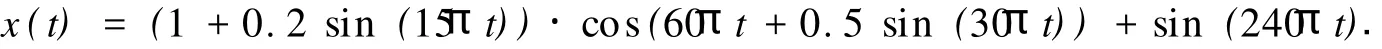
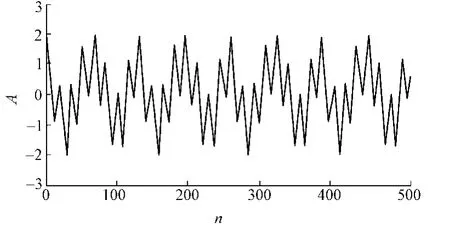
图1 仿真信号时域波形Fig.1 Waveform in time domain of simulation signal

信号由一基频为30 Hz,调制频率为15 Hz的调频调幅非线性信号和一频率为120 Hz正弦信号叠加而成.时域波形如图1所示.图1中,n为采样点数,A为幅值.对该信号进行直接EMD分解(没有进行延拓),发现该信号并不能进行有效地分解.因此,传统的方法往往要在信号进行EMD之前,进行端点延拓.

在此,选取合适的分数阶Fourier变换阶数对该信号进行分数阶Fourier变换;然后,在该分数阶变换域内对该仿真信号作EMD分解,结果如图2所示.图2中:c1组分为对应仿真信号的120 Hz频率的正弦部分;c2组分对应仿真信号的调频调幅部分;c3为残余分量.

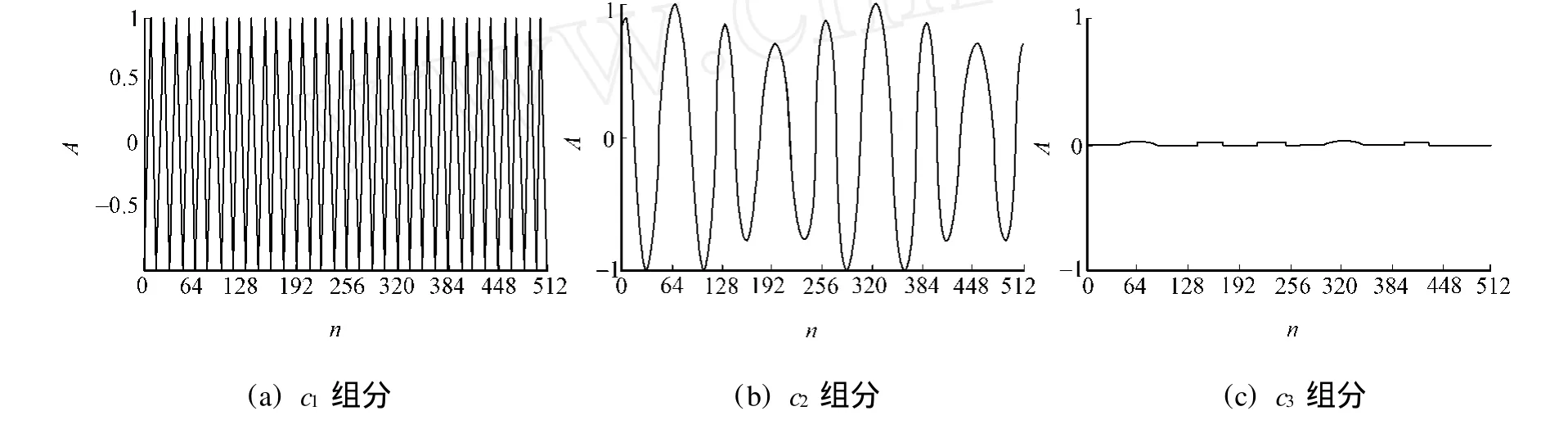
图2 仿真信号的固有模态函数Fig.2 Intrinsic mode functions of simulation signal

对仿真信号直接进行Wigner分布,结果如图3所示.由图3可知,在30 Hz与120 Hz频域之间出现了75 Hz的交叉项干扰.仿真信号在最佳分数阶傅里叶变换域中经过EMD分解后的Wigner分布,如图4所示.从图4中可看出,75 HZ的虚假频率已经消失,时频分析非常清晰准确.

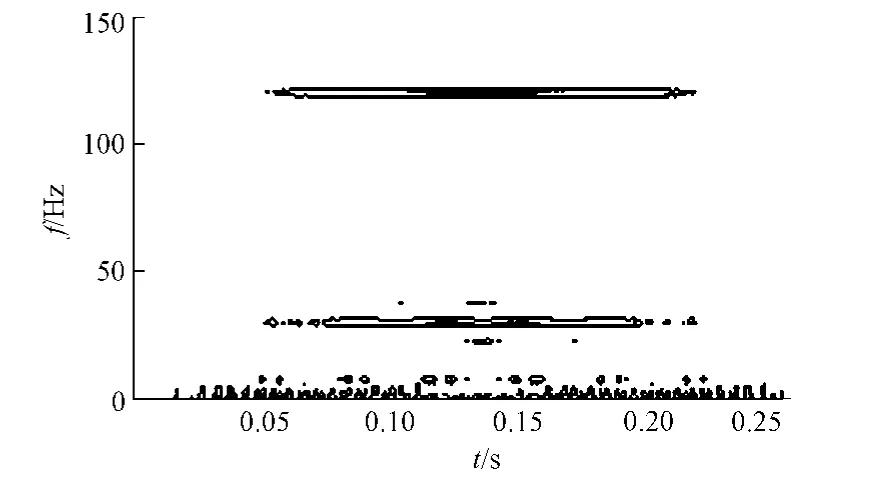
图4 基于分数阶EMD的仿真信号Wigner分布 Fig.4 Wigner distribution of simulation signal obtained by fractional EMD method

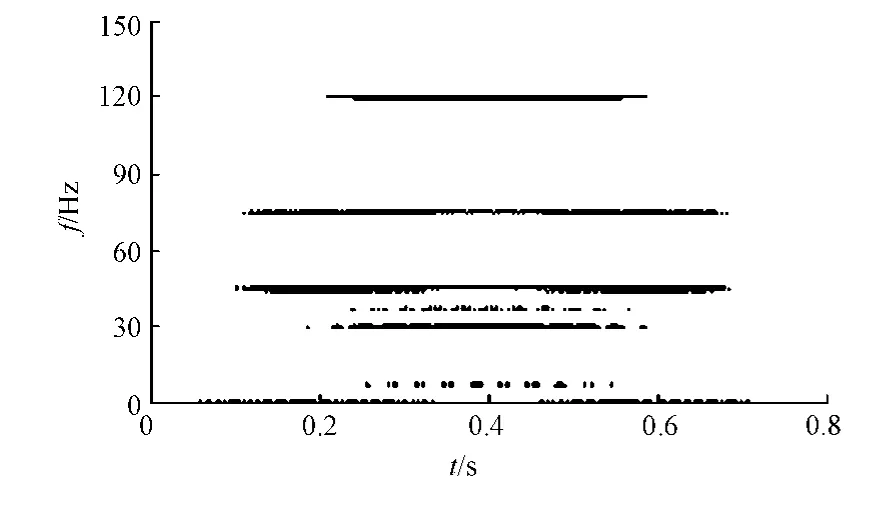
图3 仿真信号的Wigner分布Fig.3 Wigner distribution of simulation signal

4 实例验证

为了进一步验证该方法的有效性,将该方法应用到轴承故障信号处理中.实验装置见文[6],点蚀故障点是通过电火花机在轴承外圈滚道中央位置上加工微小凹坑来模拟,电动机转速为1 772 r·min-1,采样频率Fs为12 k Hz,轴承外圈故障频率为107 Hz,选取512个数据点进行分析.

图5为轴承外圈故障的时域波形.首先利用步进法确定最佳的分数阶傅里叶变换域;然后,在最佳分数阶傅里叶变换域中对故障信号进行EMD分解;最后,进行Wigner变换.故障信号的Wigner分布,如图6所示.由图6可知,故障特征频率并不明显,很模糊.故障信号在最佳分数阶傅里叶变换域中经过EMD分解后的W igner分布,如图7所示.由图7可知,故障信号的自项被很好地保留,而交叉项得到了很好的抑制,其外圈故障特征频率107 Hz明显反映出图谱的能量更加地集中.

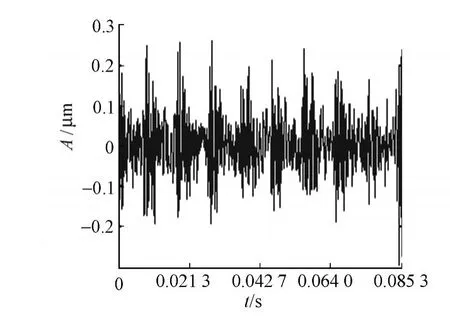
图5 故障信号时域波Fig.5 Waveform in time domain of fault signal

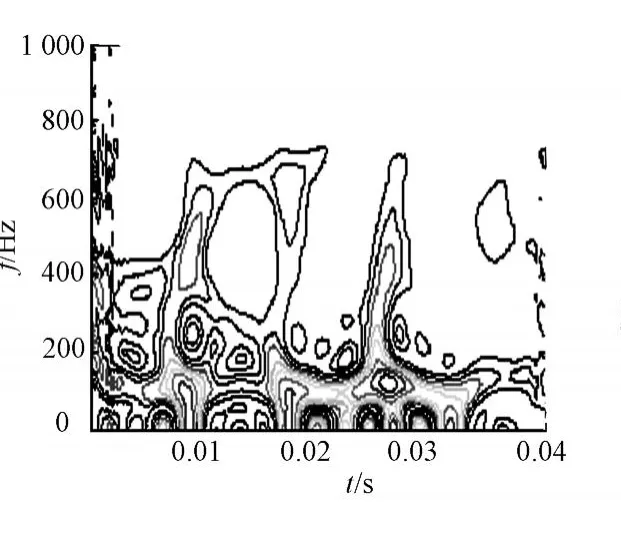
图6 故障信号的Wigner分布Fig.6 Wigner distribution of fault signal

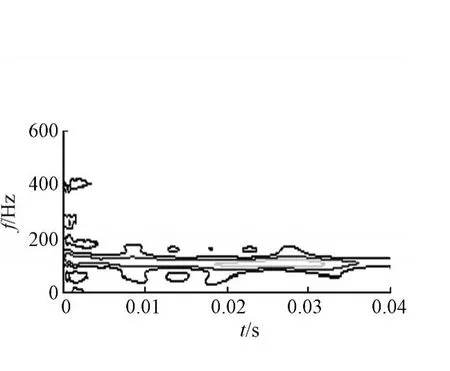
图7 分解后的故障信号Wigner分布Fig.7gner distribution offault signal obtained by fractional EMD method

5 结束语

将分数阶傅里叶变换与经验模态分解相结合,利用分数阶傅里叶变换在时频面的旋转特性,构造了分数阶傅里叶变换域的经验模态分解方法,即分数阶经验模态分解.该方法能有效地解决一类信号的经验模态分解问题,拓宽了经验模态分解方法的应用范围.仿真和实验结果表明,该方法是有效的.

[1] 刘立州.分数阶非平稳信号处理方法及在机械故障诊断中应用研究[D].郑州:郑州大学,2009.

[2] 于德介,程军圣,杨宇.机械故障诊断的Hilbert-Huang变换方法[D].北京:科学出版社,2006.

[3] HUANGN E,SHEN Z,LONG SR,et al.The empiricalmode decomposition and the Hilbert spectrum for nonlinear and nonstationary time series analysis[J].Proceedings of the Royal Society,1998,454(1971):903-995.

[4] 刘立州,王穗平,李志农,等.分数倒谱及其在机械故障诊断中应用研究[J].噪声与振动控制,2009,29(5):77-79.

[5] 吕亚平,基于时频分析的机械故障源盲分离方法研究[D].郑州:郑州大学,2009.

[6] LOPARO K A.Bearing data center[EB/OL].[2005-11-19]http:∥www.eecs.case.edu/labo ratory/bearing/dow nload.htm l.

Application of the Method of Fractional Empirical M ode Decomposition to Machine Fault Diagnosis

L IZhi-nong1,2,L IU Li-zhou2
(1.Key Laborato ry of Nondestructive Testing,M inistry of Education, Nanchang Hangkong University,Nanchang 360063,China; 2.School of Mechanical Engineering,Zhengzhou University,Zhengzhou 450001,China)

Combining empirical mode decomposition(EMD)and fractional Fourier transform,a new fault diagnosis method based on fractional empiricalmode decomposition is p roposed.The p roposed method is compared w ith the conventional time-frequency analysismethod.The simulation result show s that the p roposed method is very effective,especially fo r signal w hich can hardly be decomposed by conventional EMD method.The p roposed method rotates the signal in the time-f requency p lane,and transforms the signal from the hardly decomposable domain to easily decomposable domain,the component of the signal can be effectively extracted by EMD and fractional Fourier reverse transfo rm.The experimental results further have verified the validity of the p roposed method.

fault diagnosis;fractional Fourier transfo rm;empiricalmode decomposition;simulation

TN 911.7;TH 165+.3

A

(责任编辑:陈志贤 英文审校:郑亚青)

1000-5013(2010)04-0367-04

2009-10-19

李志农(1966-),男,教授,博士后,主要从事智能检测与信号处理、机械设备状态监测与故障诊断的研究.

E-mail:lizhinong@tsinghua.o rg.cn.

国家自然科学基金资助项目(50775208);河南省教育厅自然科学基金资助项目(2006460005, 2008C460003)