基于最小二乘拟合的墙体传热系数计算方法
【关键字】动态分析法Matlab曲线拟合 热流计法 最小二乘拟合

一 引言
在建筑物围护结构主体部位传热系数检测中,热流计法是目前国内外常用的现场测试方法。在温度和热流变化较大的情况下,采用动态分析方法可从对热流计测量数据的分析,求得建筑物围护结构的稳态热性能。
在测量中获取的数据均为随机数据,它们是由一些离散的数据组成,单就获得的原始数据本身来说根本反映不出事物的本质。如何从这些离散的数据中找出观测数据的变化规律?用Matlab进行数据的拟合可以形象直观地发现所得数据体现出来的规律性。在进行分析时,通常可采用曲线拟合法。曲线拟合法的目的是寻找一条光滑曲线,即对观测的几个变量进行多次观测,从而求出反映变量之间关系的相对函数,在某种准则下最佳地拟合数据。
二 曲线拟合的思想
如果不要求所构造的函数g(x)精确的通过所有由离散数据所确定的离散点,而只要求g(x)是给定函数类H中的一个函数,并且要求按照某种准则g(x)是相对与同一函数类H 中的其他函数而言达到最优的。即我们希望找到一条曲线,既能反映给定数据的一般趋势又不至于出现局部较大波动。在这种逼近方式下,只要所构造的近似函数g(x)与被逼近函数f(x)在区间[a,b]上的偏差满足某种要求即可。但是如何选取这个函数模型,这就是用最小二乘法解决问题的基本环节,即如何确定函数类H,也即确定g(x)所具有的具体的形式。用最小二乘法求得的近似函数逼近原来函数的效果与函数类的选取密切相关,这不是一个单纯的数学问题,还与其他领域的一些专门知识和经验有关。在数学上,通常将数据点(xi,yi)描绘在坐标纸上,然后根据这些点的分布规律选择适当的函数类。而在得不到这种信息时,我们往往选择多项式或样条函数作为拟合函数,尤其是当不知道该选择什么样的拟合函数时,通常可以考虑选择样条函数来拟合。
1.多项式拟合
有时所给的数据点的分布并不一定近似的呈一条直线,这时若仍用直线拟合显然是不合适的,对于这种情况,可以考虑用多项式拟合。多项式方程的一般形式是:
f(x)=a0+a1x1+a2x2+……+amxm
为得到函数模型,关键是解出多项式前面的系数a0,a1…am。
2.利用polyfit函数进行多项式拟合
在Matlab 中曲线拟合的形式非常简单,它的形式是:P=poly fi t(x,y,n)
该拟合函数的结果将保证在数据点上的拟合值与数据值之差的平方和最小,即满足最小二乘法准则标准的最小二乘曲线拟合。由实测数据构造n 阶多项式,并返回多项式的系数p,n 是多项式的次数,n=1 时就是线性拟合。一般说来,n+1 个数据点可唯一确定n 阶多项式。如果数据是非常准确的,那么提高拟合的次数,可以使拟合的曲线更准确。但是如果数据本身有很大的误差,则随着多项式的次数的提高,曲线将变得不够光滑,预测值将会出现较大的偏差。n 的选择随已知数据点的分布规律而定。
三 动态分析法
在建筑物围护结构主体部位传热系数检测中,热流计法是目前国内外常用的现场测试方法。在温度和热流变化较大的情况下,采用动态分析方法可从对热流计测量数据的分析,求得建筑物围护结构的稳态热性能。动态分析方法是利用热平衡方程对热性能的变化进行分析计算的。在数学模型中围护结构的热工性能是用热阻R和一系列时间常数τ表示的。未知参数(R,τ1,τ2,τ3…)是通过一种识别技术利用所测得的热流密度和温度求得的。
1.动态分析方法基本步骤如下:
测量给出在时刻(i从1至N)测得的N组数据,其中包括热流密度(qi),内表面温度(θli)和外表面温度(θEi)。
两次测量的时间间隔为△t,定义为:两次测量的时间间隔为△t,定义为:

在ti时的热流密度是在该时刻以及此前所有时刻下温度的函数:
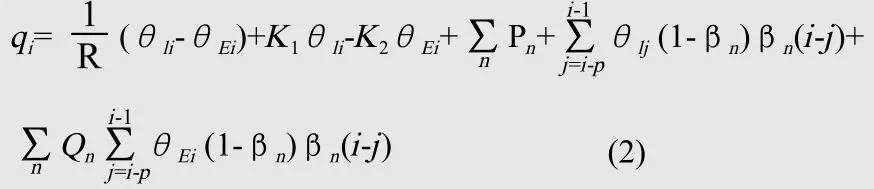
外表面温度的导数θEi与上式类似。
K1,K2以及Pn和Qn是围护结构的特性参数,没有任何特定意义.它们与时间常数τn有关。变量βn是时间常数τn的指数函数:
公式(2)中的n项求和是对所有时间常数的,理论上是一个无限数。然而,这些时间常数(τn)和βn一样,随着n的增加而迅速减小。因而只需几个时间常数(实际上有1至3个就够了)就足以正确地表示q,θE和θI之间的关系。
假定选取的时间常数为m个(τ1,τ2,…,τm),等式(2)将包含2m+3个未知参数,它们是:
对于2m+3个不同时刻下的(2m+3组)数据将公式(2)写2m+3次就得到一个线性方程组。对该方程组求解,就可确定这些参数,特别是热阻R。然而为了完成公式(2)中的j项求和,尚需附加p组数据。最后,为了估计随机变化,还需要更多组测量数据。这样就形成了一个超定的线性方程组,该方程组可采用经典的最小二乘拟合法求解。
2.Matlab数据处理过程及仿真
由公式
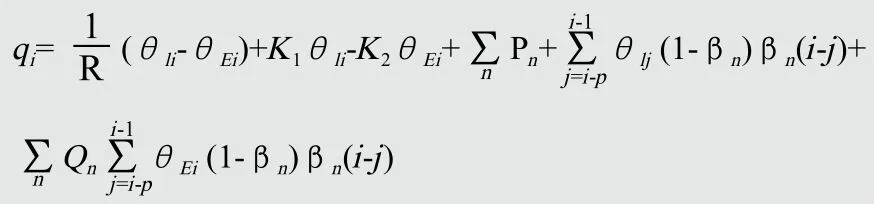
可知qi、θli、θEi为已知数,R,K1,K2,P1,Q1,P2,Q2,…,Pm,Qm未知数。
利用Matlab软件处理过程如下:
(1)输入数据:
x=[19.548 23.234 21.652 21.78 21.198 21.086 21.07 ];
y1=[26.76 26.948 26.885 26.927 26.938 26.906 26.917 ];
y2=[17.229 17.25 17.25 17.25 17.26 17.292 17.333 ];
[p1,S]=poly fi t(x,y1,1);
[p2,S]=poly fi t(x,y2,1);
p1,p2
(2)得到拟合方程
y1=0.0467x+25.9001
y2=17.2661
3.对传统方法的改进
传统的方法为算术平均法,计算如下:
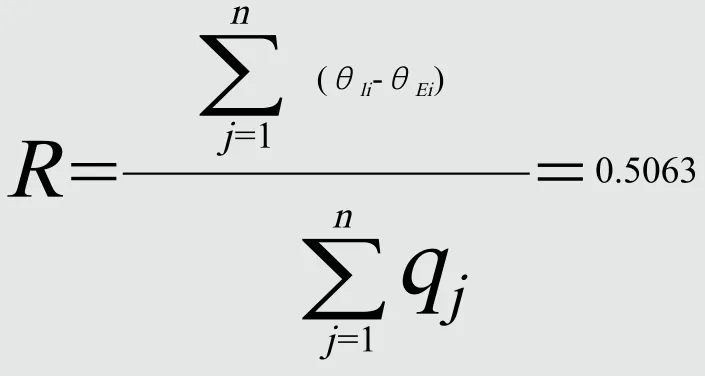
R—围护结构主体部位的热阻(m2K/W);
qj—围护结构主体部位热流密度第j次测量值(W/m2);
θli—围护结构主体部位内表面温度第j次测量值(℃);
θEi— 围护结构主体部位外表面温度第j次测量值(℃)。
最小二乘的动态分析法计算如下:
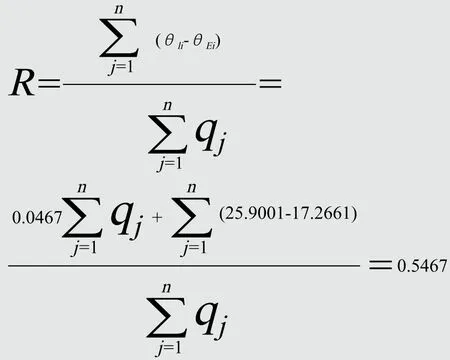
与传统的方法相比,最小二乘的动态分析法经过曲线的拟合增加了一次项,具有更高的精确度。
四 结论
利用动态分析法和Matlab软件的数据拟合工具箱对建筑物的节能检测参数数据进行了处理,并利用实际数据进行了数据仿真,并和传统的方法进行了比较。与传统方法相比较,极大的提高了检测的科学性和精确性。具有较高的实用价值。

