空间曲线曲率中心轨迹的曲率与挠率
崔凤午
空间曲线曲率中心轨迹的曲率与挠率
崔凤午
(白城师范学院 数学系,吉林 白城 137000)
研究了空间曲线曲率中心轨迹的曲率和挠率,导出其曲率、挠率与空间曲线的曲率、挠率的关系式,为深入研究曲率中心轨迹的结构奠定一定基础。
曲线;曲率中心;曲率;挠率
1 空间曲线曲率中心轨迹的曲率
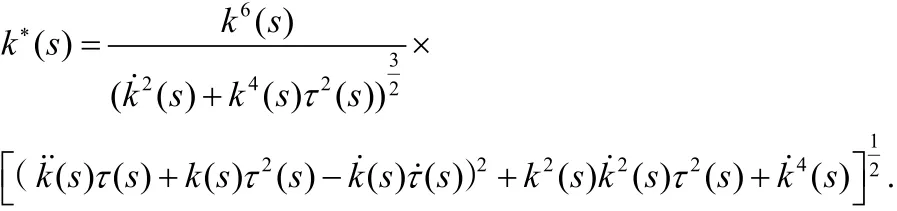
证明 由已知条件可设曲线的曲率中心轨迹方程:
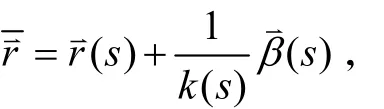
则:
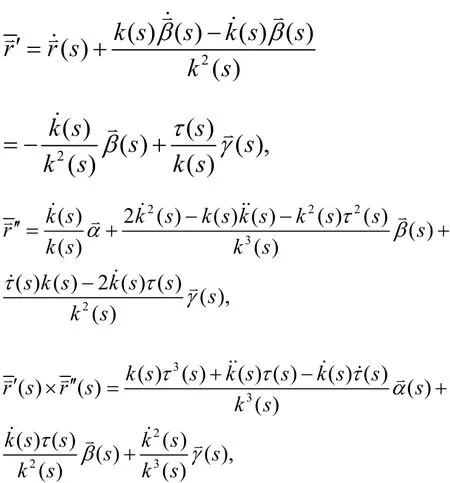
即:
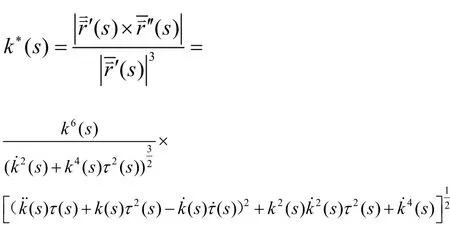
由定理1可得:
推论1 若曲线的曲率k(s)为常函数时,曲线的曲率中心轨迹的曲率与原曲线曲率相等。
2 空间曲线曲率中心轨迹的挠率
定理2 空间曲线 () r=r s⇀ ⇀ 为3
C类曲线,其中s为自然参数。若曲线的曲率为k( s),挠率为τ(s),则曲线的曲率中心轨迹的挠率为
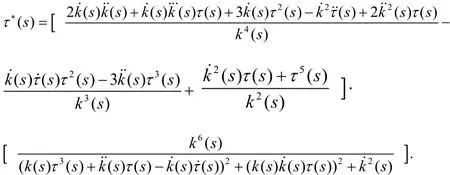
证明 由已知条件可设曲线的曲率中心轨迹方程:
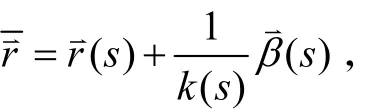
则:
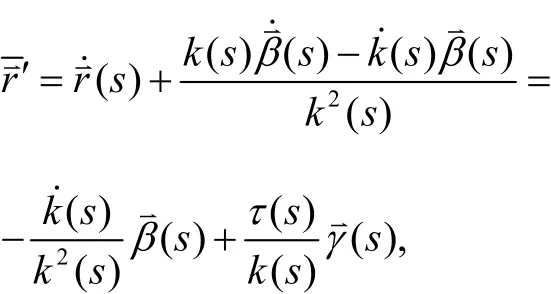
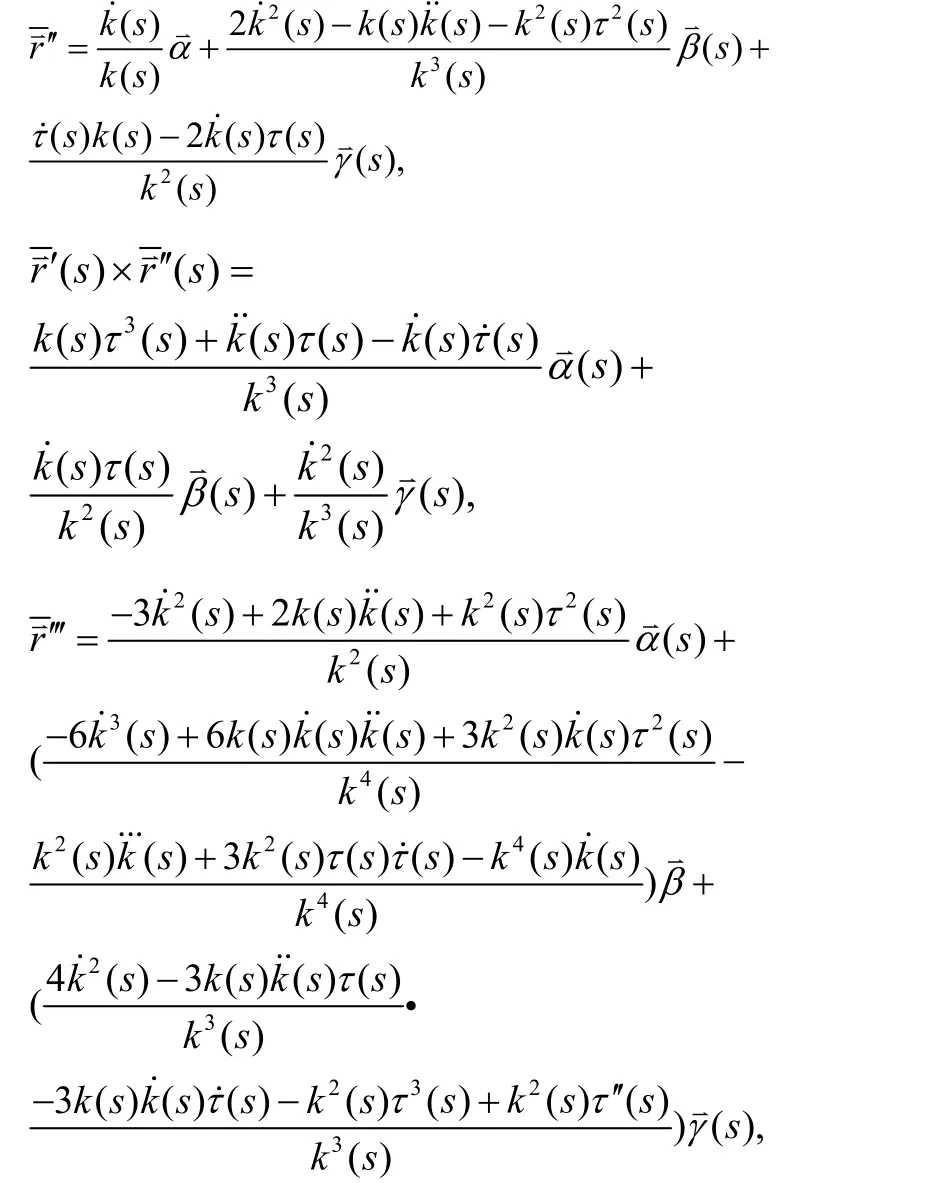
设
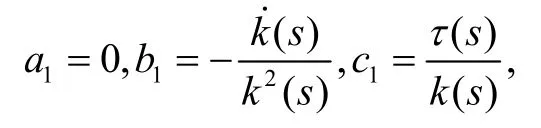
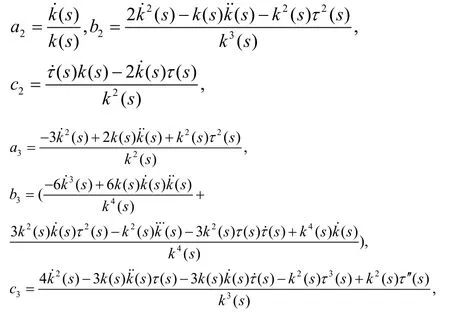
则有:
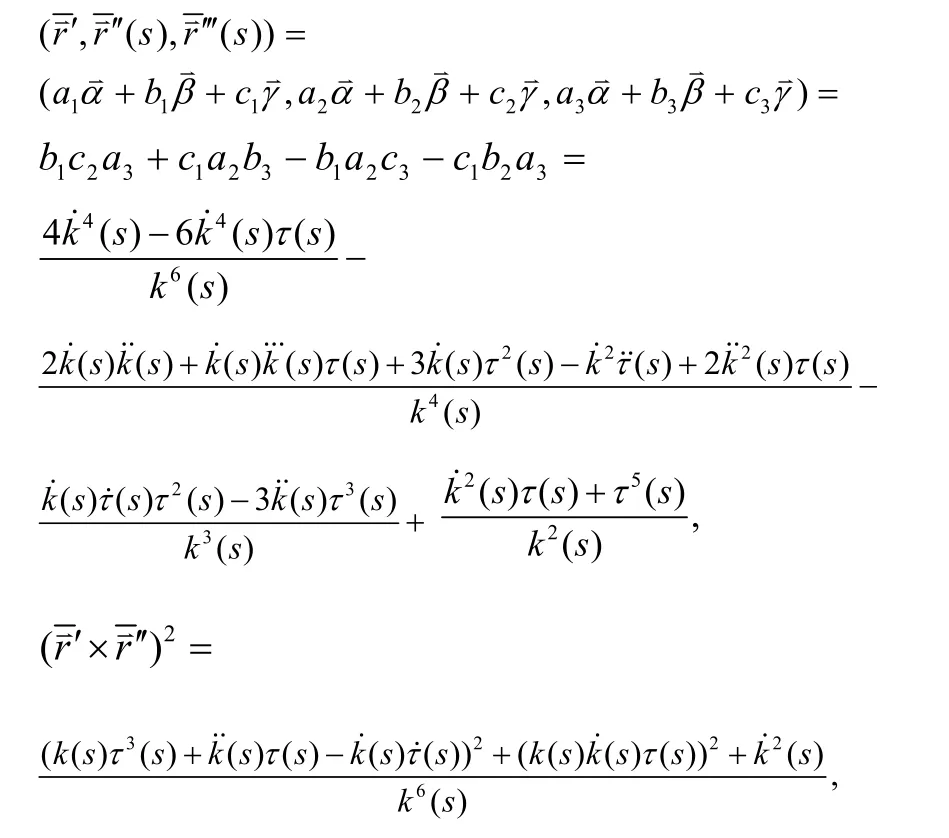
即:
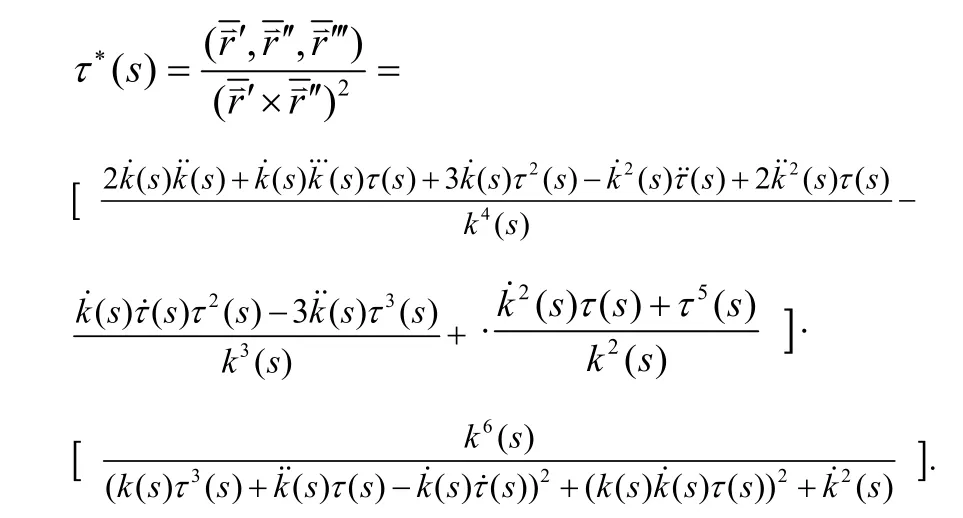
由定理2可得:
推论 2 若曲线的曲率k( s)为常函数时,曲线的曲率中心轨迹的挠率为:
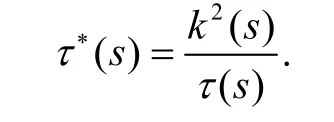
3 曲率为常数的螺线的曲率中心轨迹的结构
定理 3 曲率为常数的螺线的曲率中心轨迹为圆柱螺线。
定理1、定理2揭示了曲线的曲率、挠率与其曲率中心轨迹的曲率、挠率的关系,为研究曲率中心轨迹在一点邻近的结构奠定了一定基础。推论1 说明曲率为常数的曲线与其曲率中心轨迹弯曲程度相同。定理 3 研究了曲率为常数的螺线的曲率中心轨迹的结构,指出其曲率中心轨迹为圆柱螺线。
[1] 梅向明, 黄敬之. 微分几何[M]. 4版·北京:高等教育出版社, 2008: 5.
[2] 闫焱, 惠存阳. 给定曲率和挠率为常数的空间曲线方程[J]. 西安文理学院学报: 自然科学版, 2005(4): 24-26.
[3] Auslander L, Mackenzie R E. Introduction to Differentiable Manifolds[M]. New York: McGraw-Hill, 1963.
[4] 苏雅拉图, 李志远. 曲率和挠率的关系及应用[J]. 高等数学研究, 2008(4): 16-19.
[5] 闫焱. 关于圆柱螺线性质的一些探讨[J]. 西安文理学院学报(自然科学版), 2006(4): 45-47.
[6] 傅朝金. 空间曲线的曲率和挠率[J]. 高等函授学报(自然科学版), 2003(5): 13-14.
[7] Hicks N.J, Notes on Differential Geometry,D.Van Nostrand, Princeton, 1965.
[8] Kobayashi S. , Nomizu K. Foundations of Differential Geometry,vols. I and II[M]. New York: Interscience, 1963 and1969.
[9] Rund H. The Differential Geometry of Finsler Spaces[M]. Berlin: Springer-Verlag, 1959.
[10] Blaschke W.微分几何引论[M]. 方德植, 译. 北京:科学出版社, 1963. [11] Mishchenko A.S, Solovyev YU.P, Fomenko A.T. Problems In Differential Geometry and Topology[M]. 莫斯科: Mir出版社, 1985.
[12] Carmo M.P.do.曲线和曲面的微分几何学[M]. 田畴, 译. 上海: 上海科学技术出版社, 1988.
[13] Nutbourne A.W, Martin R.R. Differential Geometry Applied toCurve and Surface Design Vol 1[M]. 英国: Ellis Horwood有限公司, 1988.
[14] 陈省身,陈维桓. 微分几何讲义[M]. 北京:北京大学出版社, 2001. [15] 吕林根, 徐子道, 解析几何[M]. 3版. 北京:高等教育出版社, 2008. [16] 梅向明,王汇淳.微分几何[M]. 4版. 北京:高等教育出版社, 2004.
Curvature and Torsion of Trajectory in Space Curve and Curvature Center
CUI Feng-wu
(Dept. of Mathematics,Baicheng Teachers’ College, Baicheng Jilin 137000, China)
This paper studies curvature of the trajectory in space curve and curvature center by deriving its curvature, torsion and relations of curvature and torsion of space curves for further research in structure of trajectory curvature centers with established foundation to some extent.
curve; curvature center; curvature; torsion
O175
A
1009-5160(2010)02-0041-03
*通讯作者:崔凤午(1960-),男,教授,研究方向:微分几何.
吉林省教育科学规划课题《教师专业化教育的理论与实践研究》(B415017).

