求解线性方程组的一种迭代法的改进
陈丽红,周志刚,万 立
求解线性方程组的一种迭代法的改进
陈丽红,周志刚,万 立★
(武汉纺织大学 理学院,湖北 武汉430073)
对系数为对称正定矩阵的线性方程组,将文献[1]中构造的收敛迭代格式进行了改进,并给出了数值仿真结果。
线性方程组;对称正定矩阵;收敛迭代;渐进收敛速度
在科学技术、工程和经济领域中都会遇到解线性方程组的问题。求解线性方程组AX=b是科学计算的中心问题。解线性方程组主要有直接法和迭代法。对于大规模线性方程组的求解问题,特别是大规模稀疏线性方程组,迭代法是求解线性方程组的一种有效方法,它有存储空间小,程序简单等特点。线性方程组:的迭代格式一般按如下方式构造,首先将矩阵A分裂:A=A1+A2,其中A1是非奇异的且易于求逆,则方程组(1)可等价地写成:

于是方程组(1)的迭代格式可构造为:
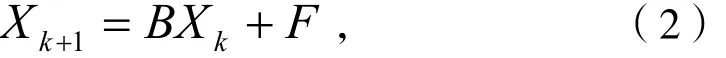
一些经典的求解线性方程组的方法如Jacobi,Gauss—seidel都是定常迭代法。不同的分裂方法可以构造多种不同的迭代算法,在多种有关文献中都有介绍。
1 定理、定义及证明
文献[1]给出如下定理:
定理[1]:如果A是对称正定n×n矩阵,则线性方程组(1)的迭代格式:
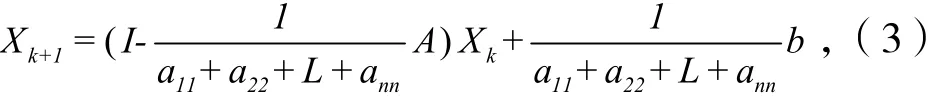
是收敛的。(证明参看文献[1])
定 义 : 迭 代 格 式 Xk+1= BXk+ F中 ,R (B)=− ln ρ( B)称为迭代格式(2)的渐近收敛速度,其中ρ(B)为B的谱半径。
定理[2]:如果A是对称正定n×n矩阵,则线性方程组(1)的迭代格式:
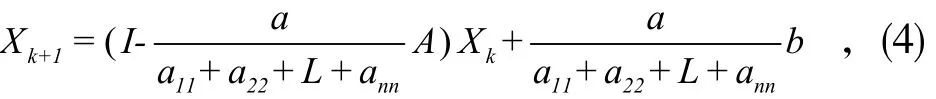
是收敛的,且渐近收敛速度比格式(3)的渐近收敛速度快, 其中,最大特征值。
证明:设 λi(i=1,2,…,n)为A的n个特征值,因A对称正定,故 λi>0(i=1,2,…,n), λ1+λ2+…+λn= a11+ a22+…+ ann, 且 存 在 可 逆 P, 使 得P−1AP = diag( λ, λ,…,λ )。于是
12n又的特征多
项式为:

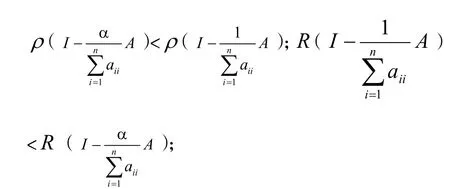
即迭代格式(4)的渐近收敛速度比格式(3)的渐近收敛速度快。证毕。
对于线性方程组(1),若A为可逆非正定矩阵,通过预处理: A:=AAT, b:=ATb,即可转化为对称正定矩阵,故上面仅讨论了对称正定矩阵。此外在定理[2]中只给出α的取值范围,而且知道在给出的范围中,α越大,迭代格式(4)的渐近收敛速度越快。在Pentium(R)4 PC、MATLAB(6.5.1版本)平台下进行数值仿真时,我们取为MATLAB软件数与数之间的最小分辨率)。
2 数值仿真结果比较及分析
下面用迭代格式(4)求解线性方程组,并与迭代格式(3)作比较。
例1 求解AX=b,其中,A=
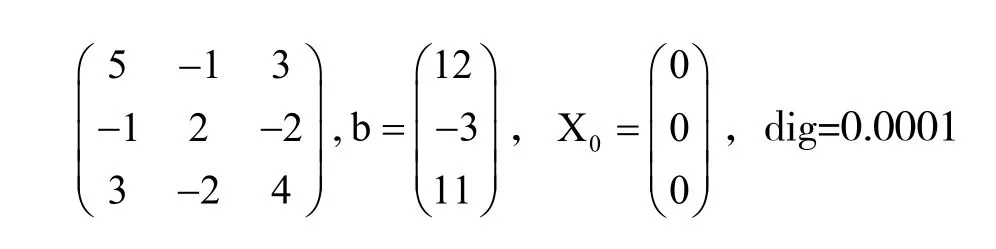
不难知道A正定,方程组的解为:(1,2,3)。文[1]已指出用Jacobi迭代格式来解此方程组时,由于迭代矩阵谱半径>1,故此格式不可取。分别用迭代格式(3)和(4)结果对比如表1。
当dig=0.000001时,格式(3)、(4)都收敛到精确解。
下面取A分别为4阶和5阶Pascal矩阵来做数值实验。Pascal矩阵为对称正定矩阵,随着阶数的增加,病态程度越严重,6阶Pascal矩阵的条件数为:1.1079e+005。
例2 求解AX=b,其中A分别为4阶和5阶Pascal
迭代格式(3)和(4)的计算结果对比见表2。在例1中,迭代格式(4)迭代次数显然比迭代格式(3)少,但多花销了点时间,随着系数矩阵 A阶数的增加,如在例2中,迭代格式(4)比格式(3)不仅迭代次数减少,而且时间花销也少,而且A阶数增加后,格式(4)比格式(3)迭代次数减少的更多,时间也花销的更少。在表2中,A为4阶Pascal矩阵时,格式(4)比格式(3)迭代次数减少了988次,时间减少了0.02s,;A为5阶Pascal 矩阵时,格式(4)比格式(3)迭代次数减少了10098次,时间减少了0.18s。因此格式(4)从整体来说比格式(3)优越。
3 格式(4)的进一步分析
在格式(4)中α的取值与系数矩阵A的最大特征值有关,因此对A的特征值的扰动必须作分析。Bauer-Fike定理 设µ是的一个特征值,且则有:其中为矩阵的p范数,p=1, 2,∞。(证明参阅文献[4])
4 结语
在迭代格式(4)中由于要计算A的特征值,我们能否利用定理:设则A的任一特征值λ满足,从A本身出发,避免计算它的特征值来对格式(4)改进,以得到更好的收敛格式是值得进一步研究的问题。
[1] 常双领, 张传林. 求解线性方程组的一种迭代解法[J]. 暨南大学学报, 2004(3): 06.
[2] 李庆扬. 数值计算原理[M]. 北京: 清华大学出版社, 2000: 307-308.
[3] Mathias R. Accurate eigensystem computations by jaccobi methods[J]. SIAMJ Matrix Anal Appl, 1995(15): 215-218.
[4] 戈卢布 G H, 范洛恩C F. 矩阵计算[M]. 袁亚湘, 译, 北京:科学出版社, 2001: 370-378.
[5] Zhang J L, Zhang X S. Neural network for linear inequalities[J]. OR Transations, 2002, 6(1): 9-18.
[6] Martin T H, Howard B D, Mark H B. Neural Network Design[M]. Beijing: K.Dai Trans.Industry Press, 2002.
[7] Zhao H M, Chen K Z. Neural network for solving systems of nonlinear equations[J]. Journal of Xidian University, 2001(2): 35-38.
[8] Burden Richard L, Faires J Douglas. Numerical analysis[M]. 7th ed. Beijing: Higher Education Press, 2001.
[9] Lou F L, Unbehauen R. Applied neural networks for signal processing[M]. London: Cambridge University Press, 1997.
[10] Abbasbandy S, Asady B. Newton’s method for solving fuzzy nonlinear equations[J]. Applied Mathematics and Computation. 2004(2): 349-356.
[11] Abbasbandy S. Extended Newton’s method for a system of nonlinear equations by modified adomian decomposition method[J].Applied Mathematics and Computation, 2005, 170: 648-656.
[12] Feiwu Chen, Daniel M Chipman. Boundary element method for dielectric cavity construction and integration[J]. J Chem Phys 2009, 119: 10289-10297.
[13] ZHOU Z G, CHEN L H Wan L. Neural Network Algorithm for Solving System of Linear Equations[J]. Proceedings of 2009 International Conference on Computational Intelligence and Natural Computing, 2009(1): 7-9.
[14] Saad Y. Numerical methods for large eigenvalue problems[M]. New York: Halstead Press NY,1992.
[15] Li Chuanguang. CGNR is an error reducing algorithm[J] . SIAM J Sci Comput, 2001, 22: 2109-2112.
[16] 张艺. 线性方程组求解的一个迭代算法[J]. 宁波大学学报: 理工版, 2001, 14 (1) : 51- 55.
Improvement of an Iterative Algorithm for Linear Equation
CHEN Li-hong, ZHOU Zhi-gang, WAN Li
(Wuhan Textile University, College of Science, Wuhan 430073, China)
A convergent iterative scheme for symmetric positive definite linear equations given by paper [1] is improved and the simulative result of numerical value is put forward.
linear equation; symmetric positive definite matrix; convergent iterative; gradual convergence rate
O241.6
A
1009-5160(2010)02-0033-03
*通讯作者:万立(1978-),男,博士,研究方向:动力系统及其稳定性理论等.
武汉科技学院校基金(093877);湖北省教育厅项目(Q20091705,2009b248);湖北省统计局项目(HB092-28).

