TiN涂层/基体接触应力的有限元分析
陈 东,谢 华,陈小文
(福州大学机械工程学院,福建 福州 350108)
TiN涂层/基体接触应力的有限元分析
陈 东,谢 华,陈小文
(福州大学机械工程学院,福建 福州 350108)
利用ABAQUS软件对在柱压头作用下 TiN涂层/基体系统的应力进行有限元分析.通过有限元解与经典 Hertz理论解的对比,验证了模型的可信度.分析了涂层厚度、涂层与基体的弹性模量比以及摩擦系数等参数对涂层/基体系统应力分布的影响.分析结果表明:在法向静载作用下,随着涂层厚度的增加或涂层/基体弹性模量比(Ec/Es)的减小,接触表面处和界面处的最大应力均减小.在切向滑动过程中,随着摩擦系数的增大,表面处和界面处的最大应力均增大.沿z轴的Mises应力在界面处的突变与Ec/Es、涂层厚度以及摩擦系数有着密切的关系.分析的结果有助于理解涂层/基体系统的失效机理,可为涂层的设计提供理论指导.
TiN涂层;Hertz接触;有限元;应力分析
TiN涂层是目前工业研究和应用最为广泛的耐磨涂层之一,由于其具有硬度高、抗氧化性能优异、抗腐蚀性强、摩擦因数低、高温稳定性和导电性良好等优点,被广泛用于模具制造、航空发动机、医学、刀具等领域[1-2].但由于 TiN涂层薄、涂层与基体的结合强度低,在受到载荷作用时,会发生表面破坏,裂纹在界面处产生、扩展,涂层与基体分离脱落而使其失效.所以,选取适当的涂层厚度以及涂层与基体的弹性模量比(Ec/Es),深入了解在载荷作用下涂层表面以及界面处的应力和应变的变化规律对于设计合理的涂层/基体结构,防止涂层失效有着重要的实际意义.
目前,对 TiN涂层/基体接触应力有限元分析并不多见,本文在基于 Hertz接触理论的基础上,借助ABAQUS软件,对在柱压头静载作用下,TiN涂层/基体系统的表面与界面处的应力随涂层厚度、Ec/Es变化的分布规律进行分析.在施加切向载荷时,分析压头在切向滑动过程中,摩擦系数对涂层应力分布的影响,对在低、高摩擦条件下,不同涂层厚度的涂层/基体系统的接触应力进行详细分析.
1 有限元模型的建立及评估
1.1 Hertz接触理论
经典 Hertz接触理论需满足以下条件[3]:(1)材料是匀质的;(2)小应变;(3)每个物体可被看做是一个弹性半空间;(4)无摩擦.
当圆柱与弹性半空间平面接触时,可得接触表面的Hertz压力为椭圆分布:

根据Johnson的接触理论,可算出在 Hertz压力作用下,表面下沿z轴应力分量:
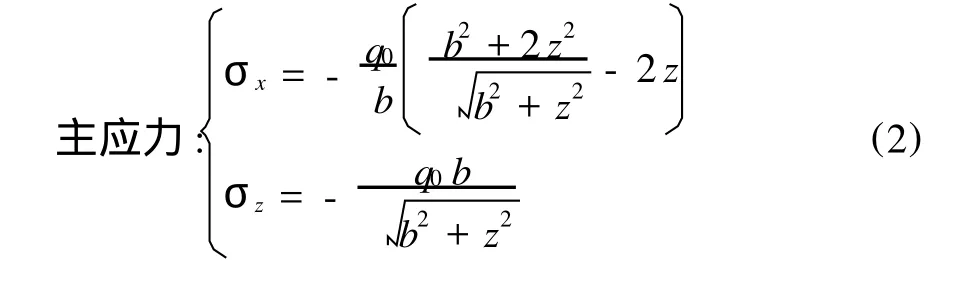

通过计算可求得:(τ1)max=0.30q0,在z=0.78b处.在柱压头作用下,由式(1)~式(3)可以画出σx,σz和τ1表面下沿着z轴变化的理论应力曲线.
1.2 模型的建立及评估
有限元分析的模型如图1所示。假定 TiN涂层与基体完美结合,将涂层和基体看做一个整体.TiN涂层弹性模量Ec=420 GPa[4],泊松比为0.25;半径R=0.1 mm的柱压头压在厚度为c的涂层上,压头为解析刚体;基体为 HSS,基体的弹性模量Es=210 GPa,泊松比为0.3.由于半空间体的几何形状依赖于接触半径b,研究表明,当半空间体宽度和厚度均取大于20b时,接触面上的载荷对系统应力分布的影响可以忽略[5].分析时在A点施加的法向静载P=10 N/mm,根据式(1)中关于b的公式计算可得b=3.32μm.半空间体(基体)的宽度和厚度均取0.1 mm(大于20b).根据对称性边界条件,C边的纵向位移(u2)为零,对称轴B边的水平位移(u1)为零,将参考点A与压头绑定,其水平位移及转角均为零.接触区域网格细分,其余部分采用渐稀式划分,由于压头是解析刚体故不必对其进行划分网格.静载单元类型为平面应变四节点四边形线性非协调单元(CPE4I),整个计算模型包含13225个单元.施加切向载荷时,考虑到在滑动中有摩擦力的存在,分析时采用二维 TiN涂层/基体系统全模型,只需将法向静载的有限元模型对称扩充即可.滑动过程中,施加法向载荷P=20 N/mm,同时沿x轴施加切向位移载荷,使压头滑动的位移从x=-6μm到x=6 μm.模型中全部采用 CPE4I,整个计算模型包含26450个单元.
由于Hertz接触理论值只适用于无涂层的基体的接触应力分布,因此将柱压头作用在无涂层基体上的结果作为有限元模型的评估,将ABAQUS计算得到的沿z轴的应力分布与 Hertz接触的理论解进行比较,结果如图2所示.由图2可知,所建的有限元模型的计算结果与经典的Hertz接触理论解结果很吻合,从而验证了有限元模型的可信度较高.
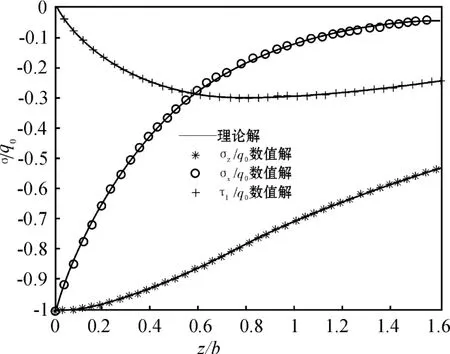
图2 无涂层模型沿z轴方向的应力理论解与数值解的比较Fig.2 Comparison of the stresses along thezaxis calculated by theoretical method and finite element method for the mode without coating
2 涂层厚度和基体弹性模量对涂层/基体系统应力的影响
2.1 涂层厚度的影响
在只施加法向静载的条件下,分析涂层厚度对接触应力的影响.图3为在不同涂层厚度下涂层/基体系统中应力分布的情况.由图3(a)可知,涂层表面径向(x方向)应力σ在接触中心处达到最大,涂层较薄时虽然稍微减少了x=0处的压应力峰值,但拉应力峰值有所增大,即增加了接触区边缘的应力变化.接触区边缘的这种应力拉压变化正是导致脆性 TiN涂层失效的主要原因.另外,在分析过程中还发现,表面剪应力相对于表面径向应力σ小得多.当涂层太薄时,涂层表面会产生过大的剪应力,较易导致表面裂纹的产生,这对系统机械性能很不利.所以在设计涂层时,既要选择合适的涂层厚度,又要选用屈服极限高的材料,同时还要兼顾基体材料的性能.图3(b)为在不同涂层厚度下,涂层/基体系统沿z轴Mises应力的分布情况.由图3(b)可知,随涂层厚度的增加,表面下沿z轴Mises应力是先减小后增大,然后再减小.由于基体和涂层弹性模量的差异,在界面处Mises应力值有较大的突变;随着涂层厚度的增加,应力梯度(突变量)是先增大后减小,当涂层厚度c=3.0μm时,应力梯度最大.涂层较薄时界面处的应力梯度虽然较小,但由于在接触边缘应力变化较大,此时涂层亦容易失效.涂层/基体系统的应力梯度过大时,涂层容易剥落,因此,在设计较厚涂层时,应尽量避开应力梯度最大的涂层厚度.由图3(c)和图3(d)可知,随着涂层厚度的增大,界面处最大剪应力和Mises应力均先增大,当涂层厚度达到临界值1.5μm时,界面处最大剪应力和Mises应力开始减小.剪应力的极值大约出现在0.8b的位置.

图3 不同涂层厚度涂层/基体系统的应力分布(a)表面处径向应力σ分布;(b)沿z轴Mises应力;(c)界面处剪应力分布;(d)界面处Mises应力分布Fig.3 The stress distribution of the coating/substrate system with different coating thicknessess(a)radial stresses(σ)at the contact surface;(b)mises stresses along thezaxis;(c)shear stresses at the interface;(d)mises stresses at the interface
2.2 基体弹性模量的影响
由于 TiN涂层的附着力随膜层厚度的增加而下降,因此 TiN膜层的厚度一般为6~8μm,制备厚的 TiN膜层十分困难[6].而涂层太薄,涂层的抗磨能力差,基体应力大,容易发生塑性变形,这时脆性的TiN涂层极易剥离失效.故在法向静载作用下,选取模型中 TiN涂层的厚度c=3μm,观察Ec/Es对涂层/基体系统的接触应力分布的影响(图4).从图4(a)可看出,随着Ec/Es的增大,表面处径向应力σ增幅明显,Ec/Es=6时,x=0处的σ=1.8q0,过大的压应力,极易导致涂层的失效.所以在设计涂层时,应注意涂层与基体的匹配.另外,分析结果表明,Ec/Es的变化,对涂层表面剪应力的影响不大.图4(b)为在不同Ec/Es下,沿z轴 Mises应力的分布情况.由图4(b)可知,涂层表面的 Mises应力比较大,界面处 Mises应力会突变,且表面和界面处Mises应力均随Ec/Es的增大而增大.Ec/Es越大,界面处Mises应力突变越明显.在实际镀膜过程中,可以先一层过渡层,或控制适当的气体成分以制备梯度涂层,通过降低弹性模量的变化梯度,来减小界面处应力的突变,提高涂层与基体的结合强度.由图4(c)可知,界面处最大剪应力随Ec/Es的增大而增大.所以在实际应用中要匹配好涂层材料与基体材料的弹性模量比,如果它们的比值过大,则容易在界面处产生过大的剪应力而使涂层剥落.随着Ec/Es的增大,界面处的 Mises应力的值亦增大(图 4(d)).
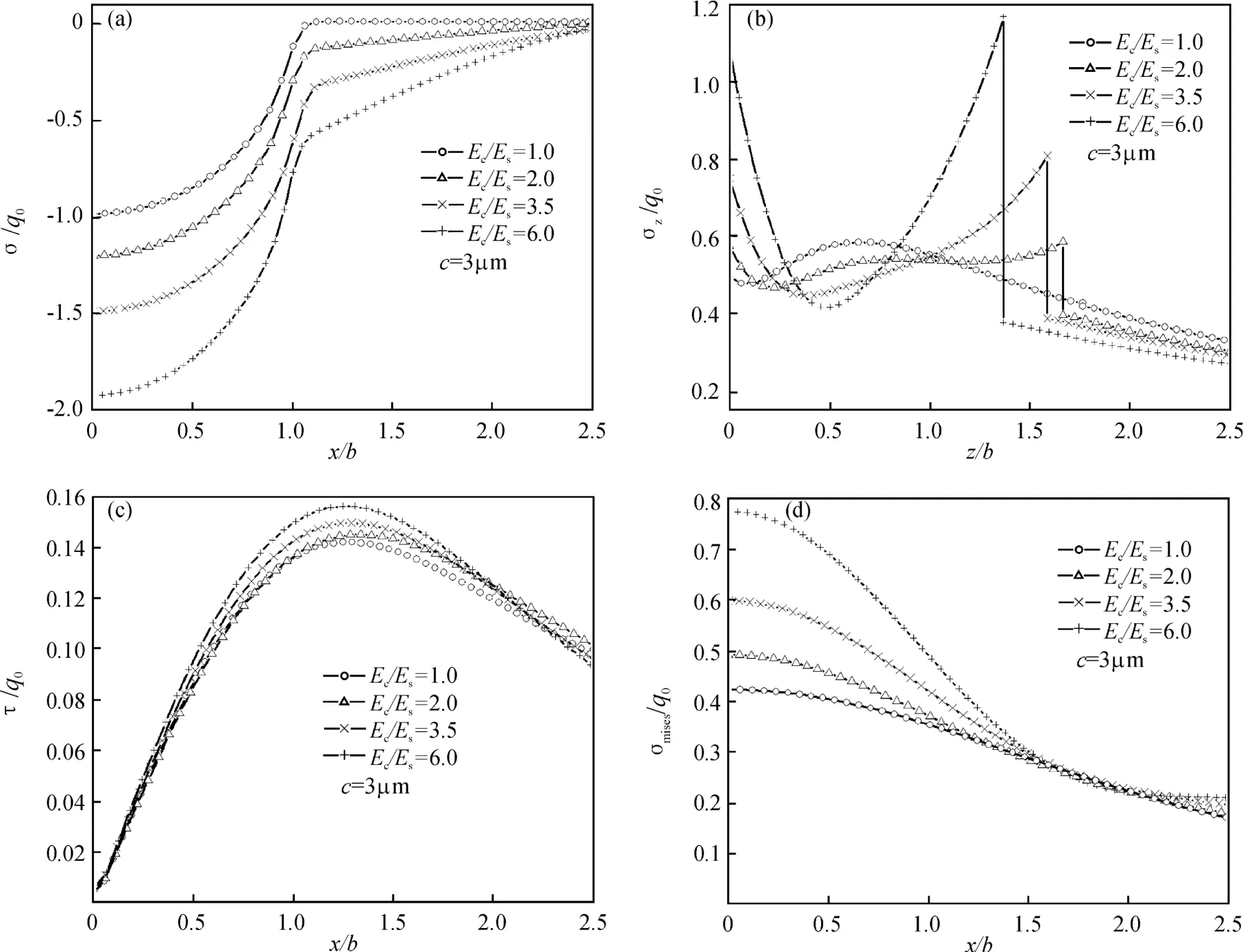
图4 不同Ec/Es下涂层/基体系统应力分布(a)表面处σ分布;(b)沿z轴Mises应力;(c)界面处剪应力分布;(d)界面处Mises应力分布Fig.4 The stress distribution of the coating/substrate system with differentEc/Es(a)radial stresses(σ)at the contact surface;(b)mises stresses along thezaxis;(c)shear stresses at the interface;(d)mises stresses at the interface
3 切向载荷作用下涂层/基体系统接触应力分布
3.1 摩擦系数对涂层表面和界面处剪应力分布的影响
以 TiN涂层厚度c=3μm,基体为 HSS,对压头施加切向位移载荷,研究涂层/基体系统在不同摩擦系数情况下,在压头切向滑动过程中,涂层接触表面以及界面处剪应力的变化.本文选择摩擦系数k为0.2,0.4,0.6,分别模拟低、中、高三种摩擦条件.图5为在不同的摩擦系数下,涂层表面及界面处剪应力的变化.从图5中可以看出,在涂层厚度一定的情况下,随着摩擦系数的增大,表面和界面处的剪应力均增大,其中表面剪应力增大的幅度比界面处的剪应力增幅大.另外,在模拟分析中还发现,界面处的Mises应力也是随摩擦系数的增加而增大的.因此,在实际应用中,应采取润滑等手段来降低接触面间的摩擦系数,以降低表面及界面处的应力,使涂层发挥最佳效用.
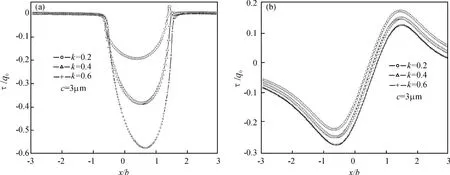
图5 不同摩擦系数下剪应力分布(a)表面处剪应力;(b)界面处剪应力Fig.5 The shear stresses distribution of different friction coefficients(a)shear stress at the contact surface;(b)shear stress at the interface
3.2 摩擦系数对不同涂层厚度的涂层/基体系统应力分布的影响
在压头切向滑动过程中,当涂层厚度变化时,分析涂层/基体系统在低摩擦系数(k=0.2)和高摩擦系数(k=0.6)下的应力变化情况.图6为低、高摩擦系数下,不同涂层厚度的涂层/基体系统界面处应力变化情况.从图6(a)和图6(b)可以看出,不论是在低摩擦还是在高摩擦下,界面处的剪应力均随涂层厚度的增大呈先增大后减小的趋势.在低摩擦系数下,这一临界涂层厚度为c=1.5μm,高摩擦系数下为3μm.另外,TiN涂层表面最大剪应力均随涂层厚度的增大而增大.高摩擦系数作用下,剪应力的增大比低摩擦系数下更加明显.从图6(c)和图6(d)可以看出,在低摩擦下,随着涂层厚度的增大,界面处Mises应力增大.当涂层厚度增大到3μm时,再继续增大涂层厚度,涂层界面处Mises应力明显降低.在高摩擦下,随着涂层厚度的增大,界面处Mises应力逐渐减小.在接触区内的Mises应力远大于接触区外的,涂层较薄时,接触区内Mises应力一直处于较大范围.而涂层厚度超过临界厚度时,Mises应力呈山峰状分布.
由图7可知,不论是在低摩擦还是在高摩擦下,界面处Mises应力突变的总体趋势是随涂层厚度的增大而增大,Mises应力的极值出现在涂层表面.在低摩擦下滑动时,界面处Mises应力的突变比在高摩擦下滑动时大很多,即摩擦系数越高,界面处突变越小,此时涂层厚度对于沿z轴界面处Mises应力突变的影响相对于摩擦系数来说小很多.

图6 不同涂层厚度的涂层/基体系统界面处应力分布(a)k=0.2时剪应力分布;(b)k=0.6剪应力分布;(c)k=0.2时Mises应力分布;(d)k=0.6时Mises应力分布Fig.6 The stress distribution at the interface of the coating/substrate system with different coating thicknesses(a)The distrubution of shear stress fork=0.2;(b)the distrubution of shear stress fork=0.6;(c)the distribution of mises stress fork=0.2;(d)the distribution of mises stress fork=0.6
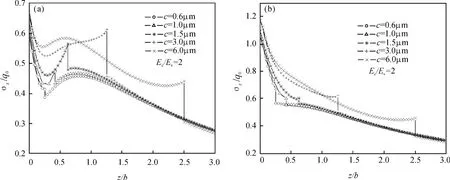
图7 不同涂层厚度的涂层/基体系统沿z轴Mises应力分布(a)k=0.2;(b)k=0.6Fig.7 The mises stress distribution along thezaxis of the coating/substrate system with different coating thicknesses
4 结 论
(1)法向静载作用下,随涂层厚度的增加,涂层表面处拉压应力变化减小,沿z轴Mises应力先减小后增大,然后再减小.涂层厚度c=3.0μm时,Mises应力梯度最大.当涂层厚度c=1.5μm时,界面处剪应力和Mises应力均为最大,当涂层厚度大于1.5μm时,继续增大涂层厚度,界面处的剪应力和Mises应力逐渐减小.
(2)Ec/Es越大,涂层表面径向应力越大.沿z轴Mises应力的突变量,随Ec/Es的增大而增大.界面处最大剪应力和最大Mises应力,随Ec/Es的增大而增大.
(3)施加切向载荷时,在涂层厚度和Ec/Es不变的情况下,随摩擦系数的增大,表面和界面处最大剪应力以及Mises应力,均随摩擦系数的增大而增大,表面处最大剪应力的增幅比较大.
(4)在高摩擦系数下,随着涂层厚度增加,界面剪应力先增大后减小;而界面Mises应力逐渐减小.在低摩擦系数下,界面处剪应力和Mises应力均随涂层厚度增加呈先增大后减小的趋势.涂层厚度的减小、摩擦系数的增大均会降低界面处Mises应力的突变量.
[1]杨世伟,曾立云,王艳华,等.(Ti,Al)N涂层的热残余应力分析[J].材料热处理学报,2006,27(3):100-103.
[2]IORDANOVAA I,KELL YB P J,MIRCHEVA R,et al.Crystallography of magnetron sputtered TiN coatings on steel substrates[J].Vacuum,2007,81:830-842.
[3]JOHNSON K L.接触力学[M].徐秉业,罗学富,刘信声,等,译.北京:高等教育出版社,1992.
[4]王强.TiN和 TiC性质的第一性原理研究[D].吉林:吉林大学,2008.
[5]STEPHENS L S,LIU Y,MRTEIS E I.Finite element analysis of the initial yielding behavior of a hard coating/substrate system with functionally graded interface under indentation and friction[J].Journal of Tribology,2000,122(2):381-387.
[6]马占吉,武生虎,肖更竭,等.电弧离子镀多层 Ti/TiN厚膜组织和力学性能研究[J].中国表面工程,2008,21(3):26-29.
Finite element analysis of the contact stress of TiN coating/substrate
CHEN Dong,XIE Hua,CHEN Xiao-wen
(College of Mechanical Engineering,Fuzhou University,Fuzhou350108,China)
ABAQUS was applied to analyse the stress of the TiN coating/substrate system with a normal load applied to cylinder indenter.The results of finite element method(FEM)and the solution of classical Hertz theoretical method were compared to prove the accuracy of FEM model.The stress in the coating substrate system has been calculated based on different thickness of coating,coating-to-substrate Young's modulus ratio and the friction coefficient.It was found when the normal stastic load was applied on the indenter,the maximum stress at the contact surface and the interface decreased with the coating thickness increasing or the coating-to-substrate Young's modulus ratio decreasing;if the indenter tangential side slipped on the coating surface,the maximum stress at the contact surface and the interface increased with the friction coefficient increasing.The gradient of Von Mises stress along the z axis strongly depended on the factors mentioned above.Analysis results are helpful to understand the failure mecheanism of the coating/substrate system well,and also can provide theoretical guidance for the coating design.
TiN coating;Hertz contact;finite element method;stress analysis
TG174.4
A
1673-9981(2010)03-0192-07
2010-05-27
陈东(1985—),男,江西九江人,硕士研究生.

