齿轮模数的现场测绘

李红英

（山西大同大学工学院，山西大同 037003）

齿轮模数的现场测绘

李红英

（山西大同大学工学院，山西大同 037003）

齿轮模数是齿轮几何尺寸计算的重要参数.对于损坏齿轮，生产现场要求准确、快速地确定其模数，以便及时配制.经过严密计算和实践验证，用公法线长度测绘法确定齿轮模数可满足要求.

齿轮模数 公法线长度 快速测绘 跨齿数 几何尺寸

齿轮箱是各类机械的变速传动部件,包含轴、齿轮、滚动轴承和紧固件等.由于制造、装配误差或不适当的条件(如载荷、润滑等)下工作,使箱中齿轮的损坏率高达60%,有齿的断裂、磨损、齿面疲劳和齿面塑性变形等,这些都会影响齿轮传动的平稳性和承载能力.因此对齿轮进行测绘,成为重新配制齿轮的重要环节.[1]

齿轮测绘就是用量具对齿轮实物的几何要素(如齿顶圆直径da、全齿高h、公法线长度Wk、中心距a、齿数z及螺旋角β等)进行测量,推算出原设计的基本参数(如模数m、压力角a、齿顶高系数h*a、顶隙系数c*及变位系数x等),并计算出制造时所需的尺寸.在维修工作中,当齿轮损坏严重,一些参数无法测得时,需要同时测量与其配对的齿轮及相关零件,根据其啮合中心距a和齿数z,重新设计齿形,以确定有关参数.

通常,在确定齿轮基本参数前,首先要了解齿轮的生产国别,认定该齿轮所采用的标准制度.其次,由于齿轮的许多参数已标准化,而且是相互关联的,所以测绘中的计算值应该与其标准值进行比较后,再确定参数值.本篇仅探讨齿轮模数的确定法.

1 齿轮标准制度的识别法[2]

(1)中国、日本、法国等多数国家生产的齿轮采用米制,即模数制,以模数m(单位为mm)作为计算齿轮几何尺寸的依据,齿轮的压力角a=20°,齿顶高系数h*a=1.0(正常齿制)或h*a=0.8(短齿制);英、美等少数国家生产的齿轮,采用英制,为径节制,以径节DP(单位为1/in)作为计算依据,其压力角a除20°以外,还有14.5°或15°,齿顶高系数h*a=1.0或h*a= 0.875.对英制产品,除航空、航海等特别精密的机器设备,为确保性能和安全可靠,应允许保留英制尺寸和参数外,其余英制尺寸原则上应换算成公制尺寸,同时要求尺寸后面保留小数点后3位数.

模数 m=p/π

径节 DP=z/d 或 DP=π/p

公英制换算公式：m=25.4/DP mm(1in=25.4mm)

式中,p-周节；z-齿数；d-分度圆直径.

(2)齿轮标准制度也可通过观察分辨齿形特征来识别.如图1所示,齿形弯曲,齿槽根部狭窄且圆弧大,为模数制;齿形平直,齿槽根部较宽且圆弧小,为径节制；齿形细长的为标准齿,齿形短粗的为短齿.短齿主要用于汽车、坦克、拖拉机、电力机车等.

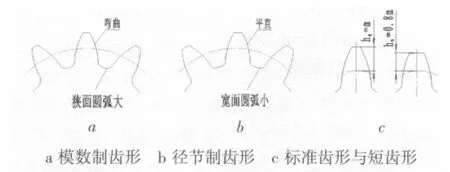
图1 齿形的识别

2 基本参数——模数的确定

模数是齿轮的一个重要参数,标准直齿圆柱齿轮各部分的几何尺寸,都是以模数、齿数和压力角三个基本参数为依据计算得到的.其中,模数是齿轮所有几何尺寸计算的基础.对于齿轮而言,齿数是显而易见的,分度圆压力角为20°,只有模数需要测绘才能得到.模数的确定方法有多种,但在测绘现场要求准确、快速地确定模数,以便及时对损坏齿轮进行配制.

2.1 齿轮模数的几何尺寸测绘法

2.1.1 用几何尺寸测量值确定齿轮模数[3]

(1)用测定的齿顶圆直径da(或齿根圆直径df)计算确定模数

1)对于偶数齿齿轮,可用游标卡尺直接测量得到da和df(如图2a所示);

2)对于奇数齿齿轮,不能直接测量得到,需要测量并计算得出.[2]

方法I:卡尺的一侧在齿顶,另一侧在齿间,测得值为da′(如图2b所示),通过几何关系推算获得da=kda′,式中k为校正系数,可由“奇数齿齿轮齿顶圆直径校正系数”表查得到.

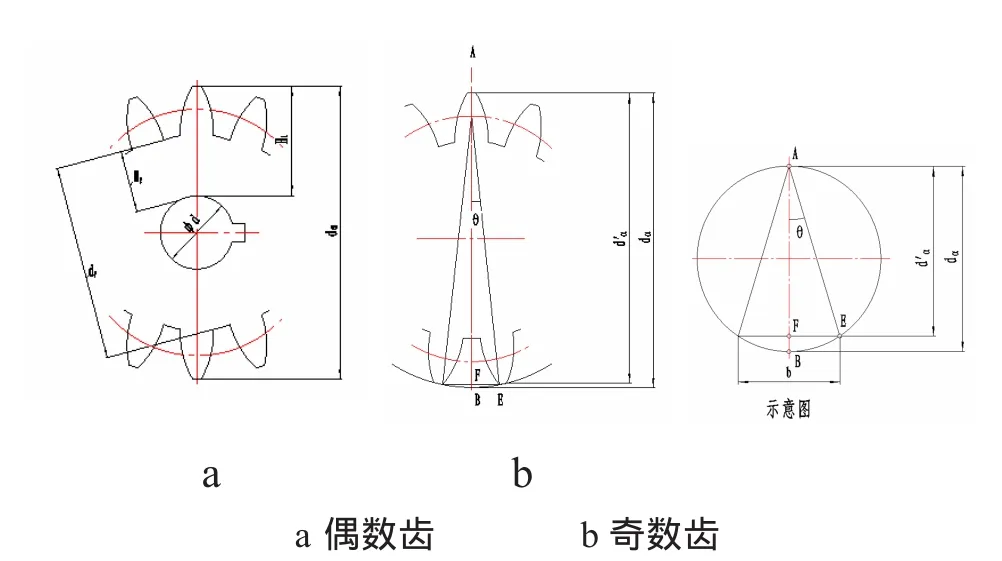
图2 齿顶圆直径da的测量

从图2 b中可看出⊿ABE中

将二式相乘得

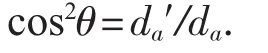
所以,da=da′/cos2θ，

取k=1/cos2θ,则da=kda′.

方法Ⅱ:对于奇数齿中间有孔的齿轮,亦可用间接测量的方法,即测量内孔直径Φd、内孔壁到齿顶的距离H1或内孔壁到齿根的距离H2(见图2 a),计算得到：

公式推导:[3][4][7]

①标准齿轮(以测绘齿顶圆直径为例)

齿顶圆直径 da=d+2ha.

因为,分度圆直径 d=m z，

齿顶高 ha=ham，

所以,da=m z+2 h*am，

故，模数 m=da/(z+2h*a)，

式中,z已知；da为可测量数值.

同理,斜齿圆柱齿轮法向模数计算公式为:

式中,β为螺旋角.

上述模数计算公式中,齿顶高系数h*a和顶隙系数c*以其标准值(正常齿h*a=1.0,c*=0.25;短齿h*a= 0.8,c*=0.3)代入进行计算,所得值m(mn)与表1“渐开线圆柱齿轮模数m”中的标准值相对照,选相符或接近的值.若差值较大,在确定测量值无误的情况下,考虑为变位齿轮.[2]

表1 渐开线圆柱齿轮模数m(GB1357—87)(mm)

②变位齿轮 (同标准齿轮相同的原理可得)

图3 中心距a的测量

⑵用测定的中心距计算确定模数

中心距a的测量如图3所示,用游标卡尺测量A1、A2,孔径Φd1和Φd2,然后按下式计算:

所以,标准齿轮的模数计算公式:

直齿轮 m=2a/(z1+z2)；

斜齿轮 mn=2a cosβ/(z1+z2).

2.1.2 几何尺寸测绘法确定齿轮模数的缺点

①计算公式复杂,难以记忆,不便于生产现场快速确定齿轮模数.

②若损坏齿轮的齿廓磨损量较大,齿顶圆直径发生变化,使da的测量值误差增大,从而使计算的模数值m(或mn)不准确;测量中心距时,由于孔的圆度、锥度及两孔轴线的平行度对中心距的影响,使测量值不准确 .[2]

③对于变位齿轮,在模数计算公式中还存在未知量——变位系数,(同时存在两个未知量:变位系数x和模数m),故无法直接确定出模数值.[4]

2.2 齿轮公法线长度的测绘

在实践中,鉴于几何尺寸测绘法确定齿轮模数的种种弊端,经过探索、计算和反复验证,在生产现场可用公法线长度测绘法准确、快速的确定损坏齿轮的模数.[5]

2.2.1 齿轮模数的公法线长度测绘法

公法线长度Wk可用游标卡尺或公法线千分尺测量(如图4所示).测量时,尽可能使卡尺的量脚平面切于分度圆附近,避免卡尺接触齿尖或齿根,这样测得的尺寸精确度高.

以测绘直齿圆柱齿轮为例[1][3][5]

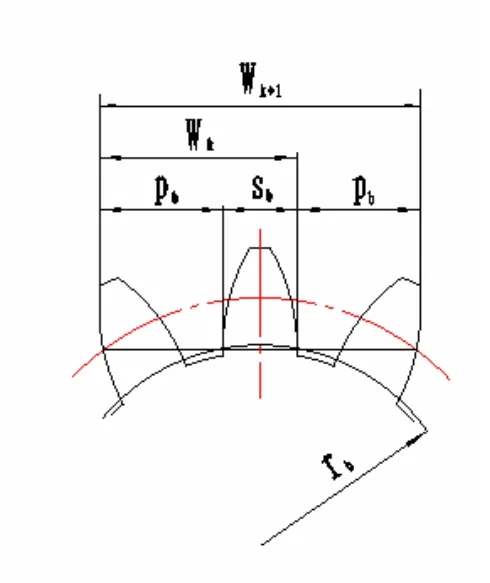
图4 公法线长度的测量

如图4所示,为标准直齿圆柱齿轮,Wk为跨齿数k的公法线长度、Wk+1为跨齿数k+1的公法线长度,rb为基圆半径,pb为基圆齿距 (基节),sb为基圆齿厚.

①标准齿轮公法线长度:

Wk=m W′=mcos a［(k-0.5)π+z inv a］，

式中,W′=cos a［(k-0.5)π+z inv a］,（可查表，

W′为m=1mm时标准齿轮的公法线长度)；

k为跨齿数；inv a为渐开线函数(可查表).

Wk+1=m W′k+1=mcos a［(k+1-0.5)π+z inv a］，

所以 Wk+1-Wk=mπcos a，

导出 m=(Wk+1-Wk)/πcos a,

可见,变位齿轮模数的确定与变位系数无关.所以，用公法线长度测绘法确定齿轮模数,其测绘公式为:m(n)≈(Wk+1(n)-Wk(n))/3.此结论对直齿、斜齿圆柱齿轮或变位齿轮都适用.

2.2.2 跨齿数的选择[6]

测量公法线时,跨齿数太多或太少都会使千分尺量脚靠近轮齿顶部或根部,形成与齿廓分度圆不相切的接触.为获得精确的公法线测量值,必须确定好跨齿数.

⑴标准直齿圆柱齿轮的跨齿数计算公式

k=0.5+za/180°，

当a=20°时,k=0.5+z/9.

⑵斜齿圆柱齿轮的跨齿数计算公式

k=0.5+z′an/180°，

当an=20°时,k=0.5+z′/9.

式中,z′是假想齿数,z′=z inv at/inv an

(an=20°时,inv at/inv an值可查表).

⑶变位齿轮的跨齿数计算公式

直齿轮 k=0.5+za/180°+2x cot a/π；

斜齿轮 k=0.5+z′an/180°+2x ncot an/π.

2.2.3 模数的测量步骤

①由k=0.5+z/9计算k值,确定k+1值,此时应注意k、k+1值必须取整数;

②用公法线千分尺测Wk、Wk+1值,考虑到公法线长度的变动误差,每次测量时,必须在同一位置,即取同一起始位置、同一方向进行测量;[2]

③由公式m(n)≈(Wk+1(n)-Wk(n))/3计算模数;④按标准化系列对模数计算值进行圆整.

3 结论

(1)公法线长度测绘法,克服了废旧齿轮齿廓磨损对测绘值的影响,提高了测绘值的准确性与模数计算值的精确度.如设齿轮磨损量为δ,[5]

因此，W′k+1-Wk′=(Wk+1-2δ)-(Wk+1-2δ)=Wk+1-Wk，从而消除了磨损误差.

(2)推导公式m(n)≈(Wk+1(n)-Wk(n))/3,k=0.5+z/9适用于不同类型齿轮模数的确定,故此公式具有计算简便,易掌握,便于现场测绘.

(3)该方法可对变位齿轮进行测绘.

[1]郑建中.机器测绘技术[M].北京:机械工业出版社,2001：131－158.

[2]张建中.机械设计基础[M].徐州:中国矿业大学出版社,2002：99－150.

[3]陈泽艮，忻良昌.公差配合与技术测量[M].北京:机械工业出版社,1986：236－254.

[4]钟秉林，黄仁.诊断学[M].北京:机械工业出版社,2005：150.

[5]郭攀成.用公法线长度测绘法确定齿轮模数的简易方法[J].机械研究与应用，2004,17（3）：26－27.

[6]朱理.机械原理[M].北京:高等教育出版社,2004：155－197.

[7]黄锡恺,郑文伟.机械原理[M].北京：高等教育出版社,1981：153－216.

[8]李晓沛,张琳娜,赵凤霞.简明公差标准应用手册[M].上海：上海科学技术出版社，2005：439－499.

M apping of G ear M odulus on the S cene

LIHong-ying
(School of Engineering，ShanxiDatong University，Datong Shanxi，037003)

The gearmodulus is an gear geometry size calculates important parameter.For the damaged gear,the requirements of produces scene accurately and rapidly determines itsmodulus so that timely fitting of a gear.Pass strictly calculated,and verified repeatedly in practice,use common normal length mappingmethod to determ ine gearmodulusmay satisfy the requirements

gearmodulus；c ommon normal length；fastmapping；cross teeth,geometry

TH132.412

A

〔编辑石白云〕

1674-0874(2010)01-0075-04

2009-08-05

李红英（1965-），女，山西原平人，实验师，研究方向：力学、金相分析及公差测量.