基于图论的自动化立体仓库堆垛机拣选路径优化

蒋丽琳，张 弛JIANG Li-lin,ZHANG Chi

（1.上海理工大学，上海 200093；2.上海汽车集团股份有限公司商用车技术中心，上海 200438）

(1.University of Shanghai for Science and Technology,Shanghai 200093,China;2.Shanghai Automotive Industry Corporation,Shanghai 200438,China)

0 引 言

自动化立体仓库采用高层立体货架储存物资，结合电子计算机控制技术和人工控制，实现货物的存储、输送、分发与管理等功能。与传统仓库相比，自动化立体仓库具有周转速度快、空间利用率高等优点。拣选作业是自动化立体仓库常用的作业方式。据统计[1]，目前国内大多数仓储中心仍属于劳动密集型产业，其中与拣选作业直接相关的人力占50%以上，拣选作业的时间投入也占整个仓储中心的30%～40%。因此，合理解决拣选作业优化调度能在一定程度上提高自动化立体仓库的运作效率。拣选作业的效率主要与堆垛机运行速度和拣选路径的选择有关。根据目前国情，拣选作业所使用的堆垛机需人工控制，速度一般要在人的可控制范围内，所以堆垛机的速度不能大幅提高。对拣选作业，国内学者一般把单个货架的拣选问题抽象成旅行商 （TSP）问题研究[2-3]，而实际拣选作业中，被拣选货品一般分散在不同的货架上。

本文结合国内自动化立体仓库的实际情况，把拣选路径构造为一种闭环作业路径，运用图论的方法进行路径优化，并对路径的优化效果进行了比较。

1 拣选作业路径模型

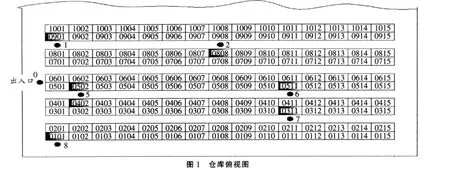
自动化立体仓库的布局如图1所示，图1显示了仓库的部分区域，共五排十五列货架，该仓库出入口处于同一位置。图中的每个小方格表示立体货架的一个单元货格的位置，方格中的数字代表单元货格的行列编号。

在堆垛机拣选开始前，由系统根据实际情况给每台堆垛机分配一定数量的货位，被分配的货位点用图1中带阴影的小方格表示。图中的实心小黑点表示堆垛机从货架上取货时，需要在仓库中停留的位置点。

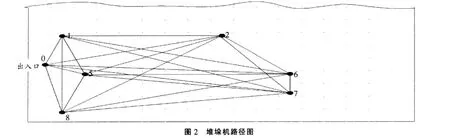
所有货位点可以汇集到同一张图上，任意两个货位点之间可以相互连接，即任意两点间都有一条路径，于是货位点和路径构成了一张完全图，如图2所示。

每两点之间的路径可以根据两点之间的到达距离来赋权值，赋权值的求解公式可以表示为：

其中，Δxij表示两货位点之间在x方向的水平距离；Δyij表示两货位点之间在y方向的水平距离，i、j表示点的编号。堆垛机的运动路径图可以用矩阵的形式表示为：

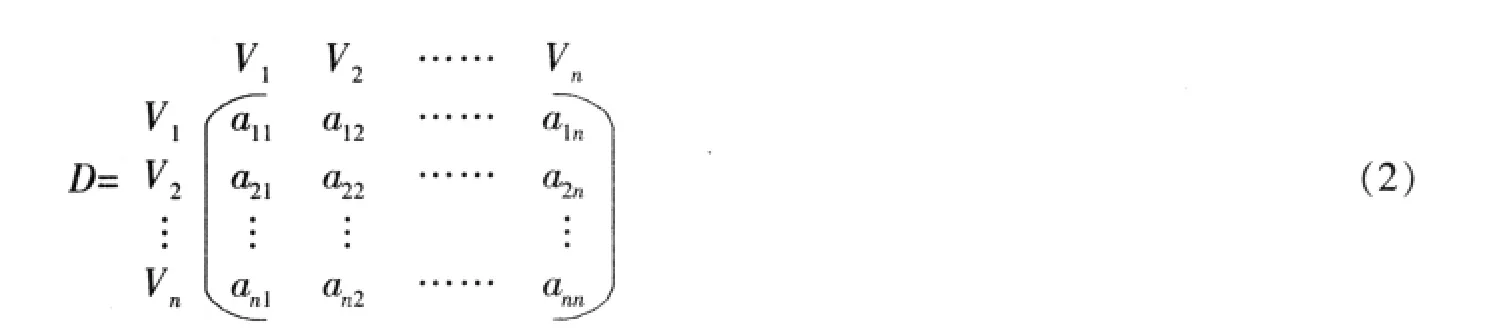
式中，vi表示第i点，aij表示第i点和第j点之间的距离。利用本文的方法，通过对各个目标货位点之间的距离矩阵的求解来实现路径的优化。

2 基于图论的仓库路径优化算法

分支定界法是解图的有限搜索的重要方法，常常用于在一个有限可供选择的解集F中，寻求其函数值为最大或最小的解。如何对解空间进行系统地搜索，依据优化的目标，尽可能多地删除一些不必要的搜索，这是分支定界的重要思想。

算法主要包含以下过程：

（1）任选初始可行解。即任选一条可行的回路，回路所含的各条路径距离的总和给原问题建立了一个上界，任何最优解均不可能超过这个上界。巡回路线总长公式可以表示为：

其中ΦT表示一条哈密顿回路，dij表示Vi到Vj的距离。

（2）确定下界。路径矩阵的行、列简化不影响最优回路的方案，若简化以后各行各列零元素构成了原问题的下界，则该回路即为最优哈密顿回路。

ai为i行简化值，bj为j列简化值。

（3）分支。若路径矩阵简化以后，零元素虽不能构成哈密顿回路，但仍可以从这些元素中选择一些边构成回路。分支边经选定设为（i,j），则在以后的讨论中可以不需要考虑，为此可以删除（i,j）所在的行列元素。（i,j）边入选回路以后，为了避免在今后的分析中，由于（i,j）边被入选而使｛（i,j）,（j,i）｝形成一个子回路。为此，降阶后的费用矩阵中dji=∞，称此类弧为禁用弧。

含（i,j）全体回路所对应的顶点的下界值便可以在降阶以后的费用矩阵中用前述方法确定。

（5）分支定界终止。连续分支定界过程，最终必可得到一条过网络全部顶点的哈密顿回路。若下界值不能剪除所有其他分支，即尚有一些分支顶点及其下届值更小，则需要回溯这类顶点，继续上述的分支。

3 算法实例

现以某立体仓库中一台堆垛机的单次拣选路径为例，以说明上述算法的使用方法及有效性。

根据货位分配原则，在拣选前首先给堆垛机分配需要拣选的货位，由货位点的位置简化得到堆垛机的停留点，两两连接各停留点，构成拣选路径的完全图模型，并根据公式 （1）为图中每条路径赋权值。路径矩阵如下：

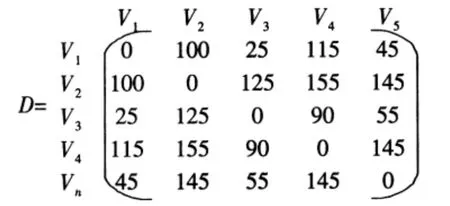
用分支定界的方法对以上数据进行处理， 任取上界路径为 ΦT=（1,2,3,4,5 ）， 则 Z（ ΦT）=100+125+90+145=460 即为上界值。

经过Matlab编程计算， 得最优哈密顿路径为｛（1,5）,（5,3）,（3,4）,（4,2）,（2,1）｝， 该路径的权值之和为Z=45+90+55+155=345。由此可见用此方法可以快速地得到比较精确的最优路径，该路径如图3所示，箭头表示行进方向。

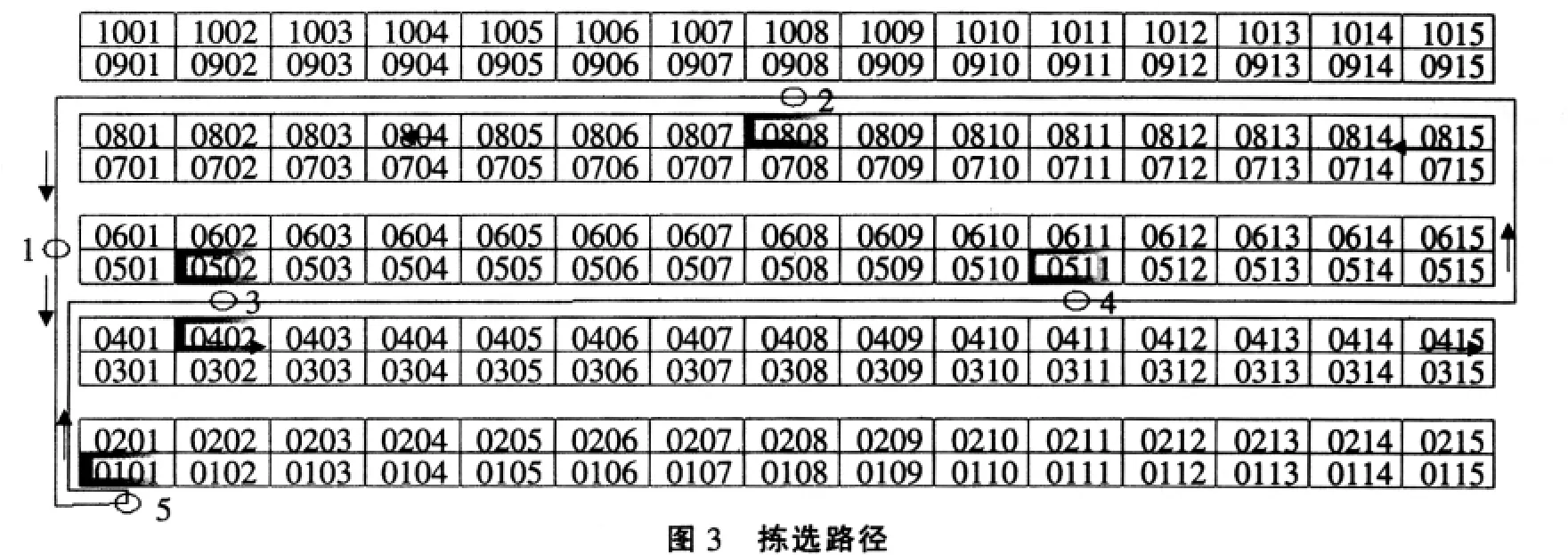
计算哈密顿路径常用的方法还有最邻近法和局部搜索法，这两种方法最大的优点是求解的速度快，计算周期短，而最大的缺点在于所得结果的精确性受到初始点的选取的影响较大。例如，对于最邻近法，本实例的计算结果为｛（1,3）,（3,5）,（5,4）,（4,2）,（2,1）｝， 权值为Z'=25+55+145+155=380。所以本文所采用的方法在起点确定的情况下能得到更加精确的解。

4 结束语

通过分析及论证，本文建立了用于规模在15个以下的自动化立体仓库拣选路径算法，并通过与传统算法结果比较，证明了本方法的优化效果。

[1]陈伊菲，刘军.仓储拣选作业路径VRP模型设计与应用[J].计算机工程与应用，2006(6)：209-212.

[2]刘增晓，冯占营，吴建,等.拣选式自动化立体仓堆垛机作业路径简易优化算法[J].起重运输机械，2006(8)：49-51.

[3]常发亮，刘增晓，辛征,等.自动化立体仓库拣选作业路径优化问题研究[J].系统工程理论与实践，2007(2)：139-143.

[4]高随祥.图论与网络流理论[M].北京：高等教育出版社，2009.

[5]Kasyanov,V.N.Graph theory for programmers[M].北京：科学出版社，2006.

[6]Fred Buckley,Marty Lewinter.图论简明教程[M].北京：清华大学出版社，2005.