毛细管中液面升降时能量转化分析
王维青
(太原师范学院 物理系,山西 太原 030031)
毛细管中液面升降时能量转化分析
王维青
(太原师范学院 物理系,山西 太原 030031)
应用变质量体系的运动微分方程,对毛细管中液面升降时能量转化情况进行了分析.
毛细管;表面张力;重力势能
毛细管插入能润湿玻璃的液体中管内液面会上升,插入不能润湿玻璃的液体中管内液面要降低.液面升高或降低,重力势能就要增加或减少,增加的重力势能从何而来,减少的势能又到哪里去了?也即能量如何转化,一般教科书限于篇幅,并不过多分析,但文献[1]的课后思考题中有这样的问题.这类问题的提出,显然对学生综合应用物理知识解决问题很有益处.
1 液体润湿不润湿固体时能量分析
液体和固体的接触面上有一个厚度为分子作用半径的附着层,对于液体能润湿固体的接触面来说,见图1(a),由于内聚力F1小于附着力F2,附着层内分子受到的合力方向与F2同向,此时附着层中的分子要进入液体中需克服分子引力做功,说明附着层中的能量要比液体中的能量低,或者讲附着层中的液体分子具有负的表面能.由玻耳兹曼能量分布律我们知道,在外界条件一定的情况下,分子总是优先地占据低能量的状态.所以液体内部分子尽量向附着层内跑,这样气、液、固接触处就形成如图1(a)所示的弯月面向上的形状.若F1>F2则相反,附着层中的能量比液体中的能量高,就有尽量减少附着层内分子的趋势,最后达到稳定时,就形成如图1(b)所示的表面形状.

图1 液体润湿不润湿固体时情况
2 毛细管中液面上升时能量分析
如图2(b)所示,半径为r毛细管插入可润湿的水中,形成凹液面,由于表面张力的存在,使凹液面下B点的压强小于大气压强,PB 图2 毛细管刚插入可润湿的液体中 图3 可润湿毛细管的液体在管中上升时情况 取如图3(a)所示的坐标系,由于液体未进入毛细管前是静止的, ∴u=0 因为要求的是能量,可把(1)式变化为: 力在x方向的投影: 把(3)、(4)式代入(2)式的左边,可得:初始:x=0,v=0;到力的平衡位置时x=h,v=v,上式积分: 其中,方程右边的质量为液体处于力平衡时的质量: 由积分的结果,可知,(6)式右边第一项为重力做的负功,也为,重力势能的增量;第二项为表面张力做的正功.显然,表面张力做功,一半用于重力势能增加,另一半由(6)式的左边可知,转化为动能了.液体在力的平衡位置时,动能不为零,也即速度不为零.显然由于惯性,液体要继续向上运动,到速度为零时,重力又比表面张力大了,在力的作用下液体又向下运动,这样就形成了振荡,定量分析如下. 为讨论方便,把x轴的坐标原点选在力的平衡位置处,则(3)式变为: 把(7)式及(4)式代入由(1)式,可得其动力学方程为: 可见,另一半动能似乎可近似地看成是用于简谐振动了,但考虑到液体的粘滞阻力,最终是耗散为热能了. 半径为r毛细管插入不润湿的水银中,形成的是凸液面,如图4,由于表面张力的存在,使凸液面下B点的压强大于大气压强,pB>po.这样毛细管内的液体就要向下运动,直到下降到h满足pB=po+ρg h为止.此时,毛细管内的液面在C处,以B点所在处为上表面,以C所在处为下表面,隔离出一个底面半径为r的液柱,显然,随液柱下降,其质量是减小的.但由于液柱下面的液体仍在毛细管内,随液柱一起运动.所以(1)式中的u=v.由图4(b)所示的坐标,可得质量的表达式: 其受到的三个力如图所示,因pB=pC,所以实际液柱仅受到重力,即: 图4 不润湿毛细管的液体在管中下降时情况 将(12)式、(13)式代入(1)式,并整理可得: 初始:x=,v=0;到力的平衡位置时x=h,v=v,上式积分: 结果说明,重力做正功,使重力势能减小,减小的能量变成动能.即在力平衡位置时速度不为零,由惯性液体继续向下运动,直到速度为零时,B点所在处的压强又比h深处大, 使液体又受到向上的力,结果同样在平衡位置振荡.因在力平衡位置时,小液柱的质量为零了,所以要得振动方程就不能以C处为液柱的下底面了.取毛细管的下端处为小液柱的下底面,还看图4(b),这样,又有u=0,但液柱受到的合力: 将(16)、(17)式代入(1)式,可得: 不考虑粘滞阻力时,仍可近似为简谐振动. 总之,毛细管内液面升高时,表面张力做正功,使重力势能增加;液面下降时,似乎表面张力应做负功,使重力势能减小,但这里选取的研究对象正好使上下液面的压力抵消.若小液柱的下底面没选在力的平衡位置,如选在A处,显然表面张力是要做功了. 〔1〕秦允豪.热学[M].北京:高等教育出版社,1999:304. 〔2〕陈世民.理论力学简明教程[M].北京:高等教育出版社, 2008:109. O 35 A 1673-260X(2010)07-0014-02


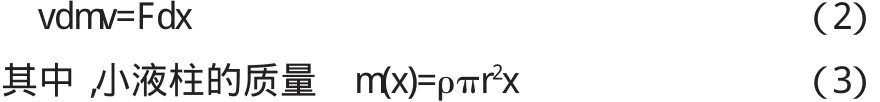





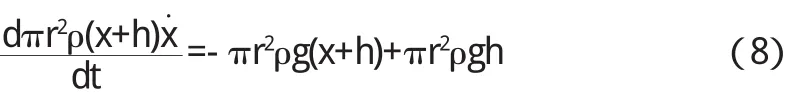


3 毛细管中液面下降时能量分析