基于自抗扰控制器的异步电机调速系统

刘丽英，姚青梅，张翠敏，林 林，赵 泳

（天津工程师范学院自动化与电气工程学院，天津 300222）

基于自抗扰控制器的异步电机调速系统

刘丽英，姚青梅，张翠敏，林 林，赵 泳

（天津工程师范学院自动化与电气工程学院，天津 300222）

设计了一个基于自抗扰控制器的异步电机调速系统。由于自抗扰控制器的结构，决定了其不需要异步电机精确数学模型，即能够通过扩张状态观测器估计出电机模型中的耦合项及参数摄动等引起的总扰动并加以补偿，实现磁链和转矩的完全解耦，再加上自抗扰控制器中非线性函数的使用，使系统具有非常好的动、静态性能和参数鲁棒性。仿真结果表明：自抗扰控制不仅无超调、响应速度快、静态无误差，且对负载扰动、电机参数变化等具有很强的鲁棒性。

异步电机；自抗扰控制器；扩张状态观测器；鲁棒性；仿真

20世纪60～70年代，随着电力电子技术的发展，使高性能交流调速系统应运而生。这时，交流电动机具有的结构简单、成本低廉、工作可靠、维护方便、惯量小、效率高等优点也日益显露出来，尤其是20世纪70年代初发明了矢量控制技术，使交流传动系统可获得与直流传动系统同样优良的动、静态性能，交流调速系统从而在工业中得到广泛的应用。然而，由于在实时控制中存在严重的外部干扰、参数变化和非线性不确定因素，基于精确电机参数的准确解耦很难实现，实际控制效果难以达到理论分析的结果[1]。另外，基于现代控制理论的高性能异步电机调速方法主要是依靠精确的数学模型加上传统的PID控制，它们在实际中已有较好的应用，但是它们都有对负载变化的适应能力差、抗干扰能力弱和受系统参数变化影响等弱点，而且异步电动机具有非线性、强耦合、多变量等特性，很难用精确的数学模型描述，这就使得基于精确数学模型的传统控制方法面临着挑战。针对上述问题，本文将文献[2]提出的自抗扰控制器（ADRC）引入异步电机调速系统。

自抗扰控制技术是在吸取PID的优点、克服其缺点的基础上发展而来的[3]。自抗扰控制器的结构决定了它不需要被控对象的精确数学模型，通过扩张状态观测器即能实时估计系统在运行过程中受到的各种扰动的总和并加以补偿，从而提高系统的性能。文中在MATLAB/SIMULINK环境下对基于自抗扰控制器的异步电机调速系统进行了仿真研究，结果表明，自抗扰控制具有非常好的动、静态性能和参数鲁棒性。

1 自抗扰控制器（ADRC）

由于二阶自抗扰控制器用得较多，所以下面以其构成的系统为例说明自抗扰控制的原理。

设一类不确定对象为：

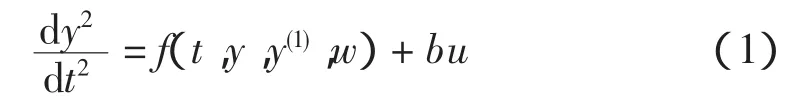
式中：w（t）为扰动；f（·）为未知函数，它包含了系统中所有的不确定项；b是常数；y为对象输出；u为控制量。由自抗扰控制器构成的控制系统如图1所示。

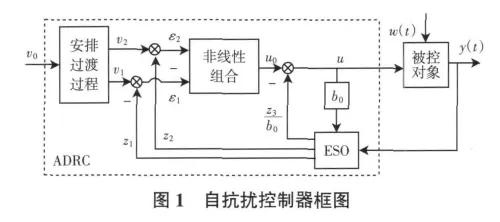
从图中可以看出，自抗扰控制器[2-6]由4部分组成：安排过渡过程、扩张状态观测器、非线性组合和扰动补偿。

安排过渡过程作用是输入1个参考信号v0，输出2个信号。v1是v0的跟踪信号，但变化缓慢了，类似给定积分器的效果，因此在经典调节理论中因设定值的突变而造成的控制量的剧烈变化以及输出量的超调也避免了。v2是v0的微分信号，其数学模型为：

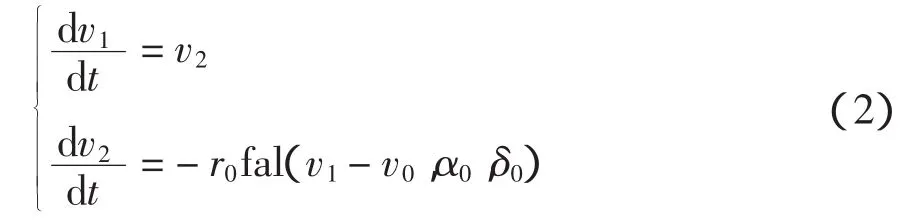
扩张状态观测器和扰动补偿是自抗扰控制器的核心部分，扩张状态观测器估计出对象的各阶状态变量和对象总扰动实时作用量（内扰和外扰），并由扰动补偿环节加以补偿，从而使系统线性化为积分器串联型结构，简化了控制对象，提高了控制性能。其中，z1、z2跟踪对象状态变量，－z3/b0起着扰动的“补偿”作用。

把式（1）写成状态方程形式如式（3）所示：

式中：x3=f是未知的被扩张的状态变量；h（t）是f（·）的导数，是未知的；b0是对象的控制输入放大系数b的粗略估计值，即b0≈b。与式（3）相应的扩张状态观测器为：

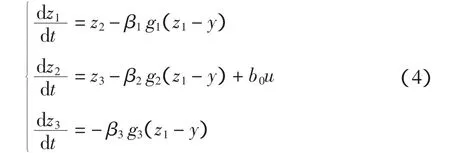
式中：β1、β2和β3是观测器增益；g1、g2和g3是非线性函数。例如：

非线性组合是安排过渡过程和扩张状态观测器的相应输出之间误差的非线性组合，它能使稳态误差以指数形式成数量级减小，因此可以取消积分环节，积分的副作用也就避免了。其数学模型为：

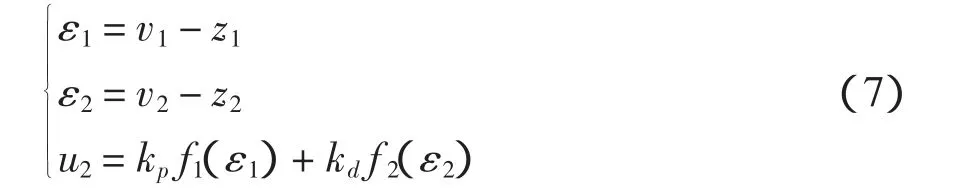
式中：kp和kd是控制器增益；f1和f2是适当选取的非线性函数，也可取式（5）表示的函数。

2 基于ADRC的异步电机调速系统设计

基于转子磁场定向理论，笼式异步电动机在同步旋转坐标系下的动态模型可用四阶非线性微分方程来描述：

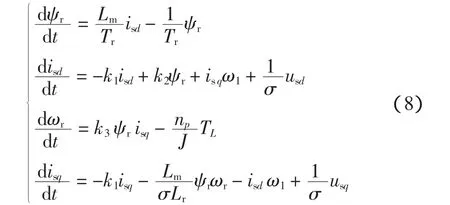
令w1（t）=k2ψr+isqw1，w2（t）=-（np/J）TL和w3（t）= -（Lm/σLr）ψrωr-isdω1，则式（8）变为式（9）的线性结构：

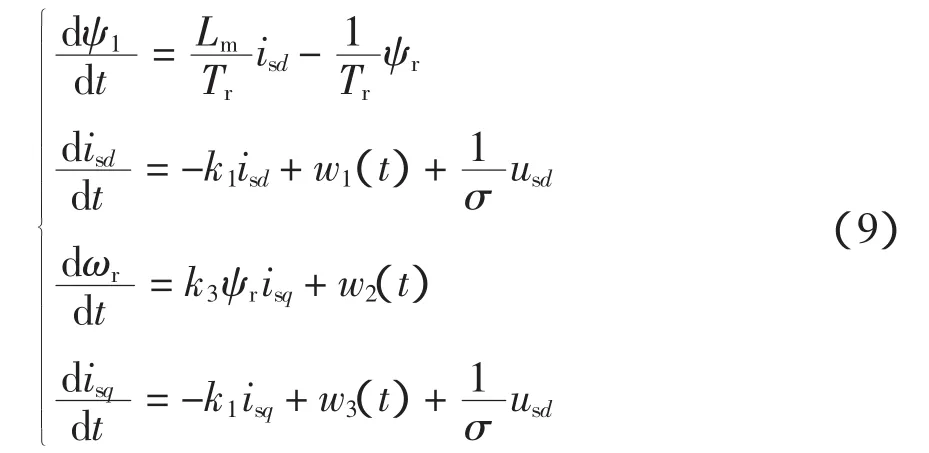
实际使用时，需对励磁电流和转矩电流进行限幅控制，因此采用图2所示的由4个一阶自抗扰控制器分别调节的双闭环控制方案。

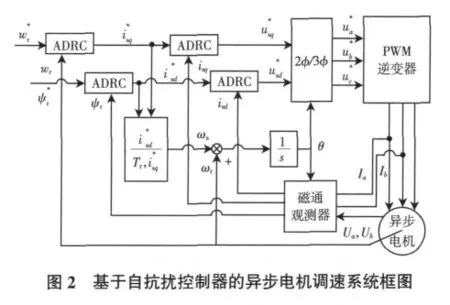
以d轴电流为例说明一阶自抗扰控制器的结构。

非线性组合：u0=kfal（v1-z1，α，δ）

扰动补偿形成控制量：u=u0-z2/b0

式中：r、α、δ、β1、β2、k、b0是控制器的参数，b0=1/σ，

3 仿真研究

为了验证采用自抗扰控制器后异步电机调速系统的性能，在MATLAB/SIMULINK中进行仿真研究。电机的参数如表1所示。电流的幅值取20 A，电压的幅值取340 V。图3和图5的转速为标厶值，其中nbase=1 460 r/min。

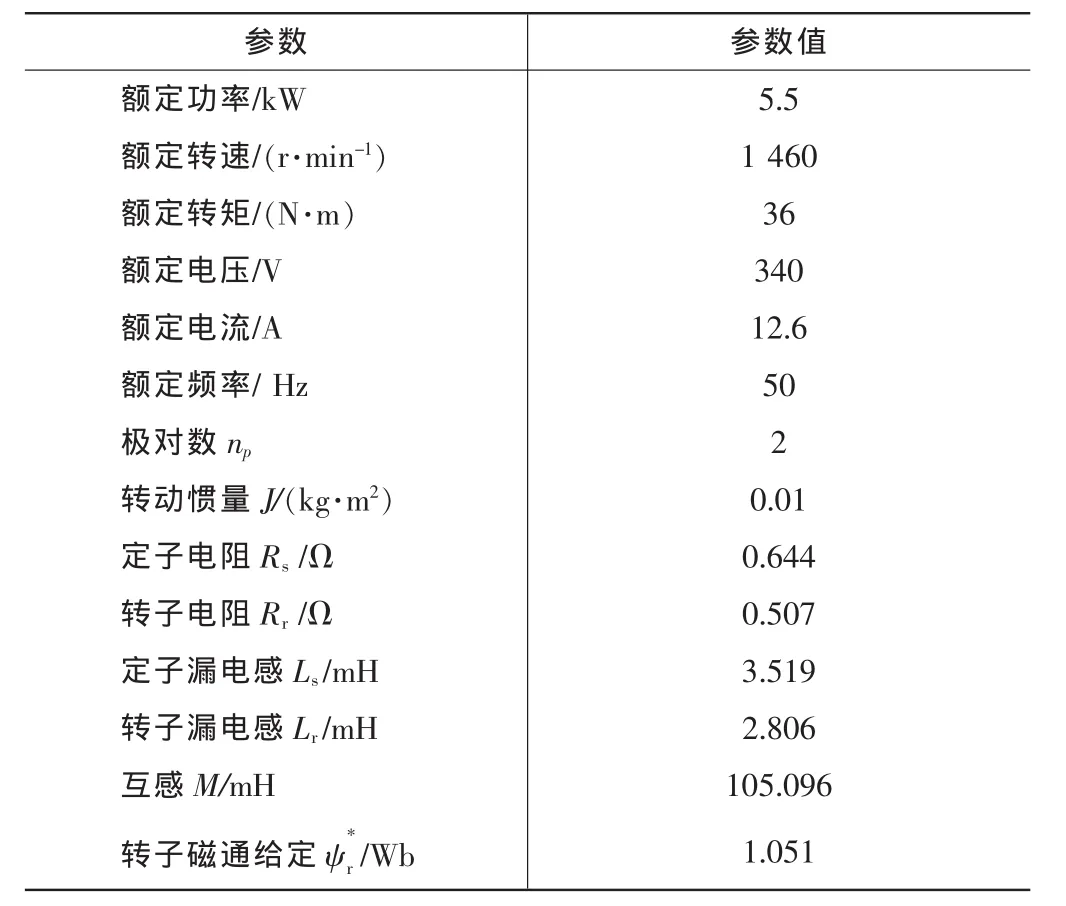
表1 电机参数

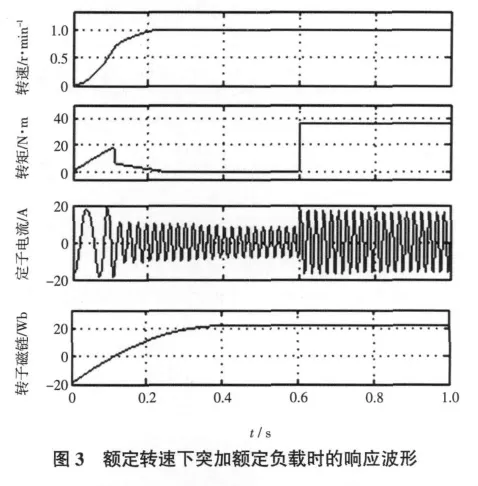
给定转速为1 460 r/min，空载起动，负载在0.6 s时突变为额定值时的波形，如图3所示。由图3可以看出，系统起动无超调，稳态无静差，动态速降约2%，恢复时间约0.2 s，突加负载时各量没有受任何影响，说明系统具有非常好的动、静态性能。

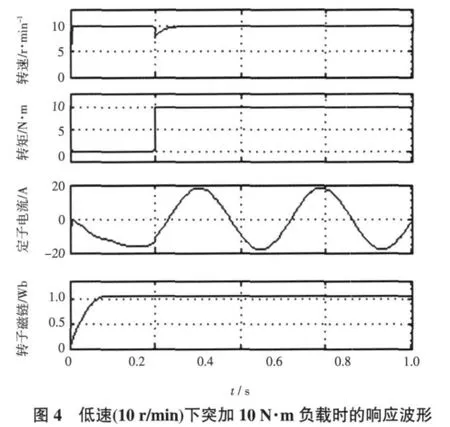
给定转速10 r/min，空载起动，负载在1 s时突变为10 N·m时的波形如图4所示。由图4可以看出，系统起动无超调，稳态无静差，动态速降约20%，恢复时间约0.3 s，突加负载时各量同样没有受任何影响，说明系统在低速下一样具有非常好的动、静态性能。图5是为了验证ADRC对系统参数变化的鲁棒性和自适应性，在730 r/min下空载起动，1 s时转子电阻值由0.507 Ω突增为0.707 Ω、转动惯量由0.01 kg·m2突增为0.05 kg·m2时的波形。

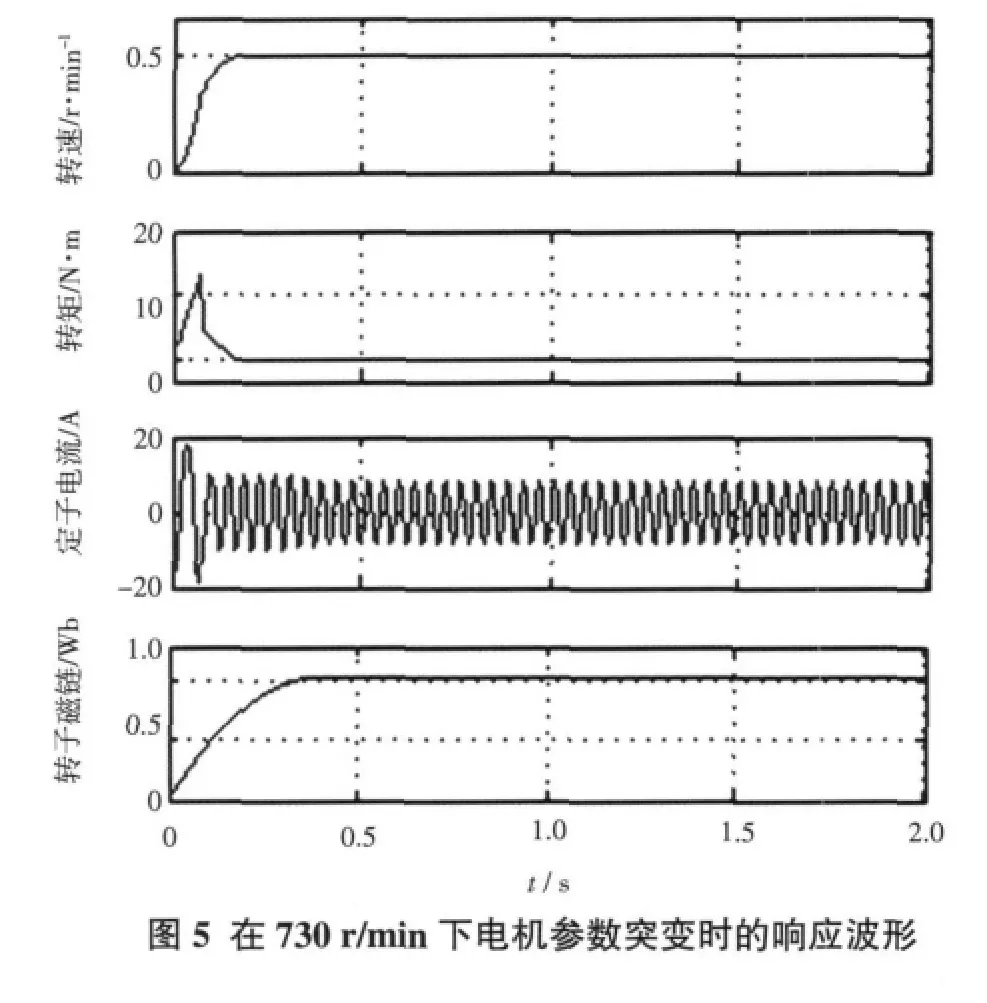
由图5可以看出，转子电阻和转动惯量同时突变时，各个量都没有受任何影响，说明ADRC对参数变化具有非常强的鲁棒性和自适应性。

4 结论

针对异步电机难以建立精确的数学模型和矢量控制系统参数鲁棒性差的问题，在分析异步电机数学模型和自抗扰控制原理的基础上，将自抗扰控制器应用于异步电机的控制中，实现了异步电机调速系统的自抗扰控制。仿真结果表明：自抗扰控制器具有非常好的动、静态性能和参数鲁棒性，是能够替代PID控制技术的、新型实用控制技术。

［1］ 葛宝明，王祥珩，苏鹏声.交流传动系统控制策略综述[J].电气传动自动化，2001，23（4）：3-9.

［2］ 韩京清.自抗扰控制技术[J].前沿科学，2007（1）：24-31.

［3］ 韩京清.从PID技术到自抗扰控制技术 [J].控制工程，2002，9（3）：13-18.

［4］ GAO Z Q，HUANG Y，HAN J Q.An alternative paradigm for control design[C]//Proc of the 40 th IEEE Conference on Decision and Control.Orlando：FL，2001：4578-4585.

［5］ GAO Z Q，HU S H，JIANG F J.A novel motion control design approach based on active disturbance rejection[C]// Proc of the 40 th IEEE Conference on Decision and Control. Orlando：FL，2001：4877-4882.

［6］ 夏长亮，李正军，杨荣.基于自抗扰控制器的无刷直流电机控制系统[J].中国电机工程学报，2005，24（2）：82-86.

Induction motor drive based on active disturbance rejection controller

LIU Li－ying，YAO Qing－mei，ZHANG Cui－min，LIN Lin，ZHAO Yong
（School of Automation and Electrical Engineering，Tianjin University of Technology and Education，Tianjin 300222，China）

An induction motor drive based on active disturbance rejection controller（ADRC）is designed in this paper.The structure of ADRC makes it unnecessary to have the accurate mathematical model.The induction motor drive can estimate and compensate the integral disturbance caused by coupled model and parameter perturbations，achieving the decoupling between flux and torque,by the extended state observe（ESO），Moreover，the activ use of nonlinear functions makes ADRC have better performances and robustness.Simulation results show that disturbance rejection control has no overshoot，no static error with fast response，but also has highly robust for load disturbances and parameters.

induction motor；active disturbance rejection controller；extended state observer；robustness；simulation

book=2,ebook=93

TM343

A

1673－1018（2010）02－0016－04

2010－03－10

天津工程师范学院科研项目（YY09005）.

刘丽英（1976—），女，讲师，硕士，研究方向为电机控制.