四元数形式的Jacobi猜想

刘 华，屈非非

（天津工程师范学院 理学院，天津 300222）

四元数形式的Jacobi猜想

刘 华，屈非非

（天津工程师范学院 理学院，天津 300222）

从超复分析的角度考虑Jacobi猜想，设P（w）=（p1（w），p2（w））是二维复空间到自身的多项式映射，研究四元数的左全纯多项式f（z1，z2，z3）=p1（w）+jp2（w），其中w=（x0+x1i，x2+x3i）和z1=x1-x0i，z2=x2-x0i，z3=x3-x0i。这显示了用四元数中的全纯函数的技巧处理Jacobi猜想是一条可能的途径。

四元数分析；左全纯函数；Jacobi猜想

用H表示实四元数所构成的skew域，即在四维实线性空间上定义一个以1，i，j，k（也记作e0，e1，e2，e3）为生成元的乘法结构，它们满足：

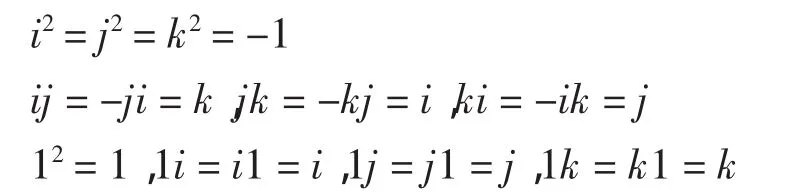
而H中的元素，q=x0+x1i+x2j+x3k，（x0，x1，x2，x3）之间的乘法按结合律和分配律用上式来展开[2]。在本文中，有时也写x=x0+x1i+x2j+x3k，从上下文来看不会混淆。

设域Ω⊂H，f：Ω→H为实可微函数。如果f满足以下Cauchy–Riemann方程：

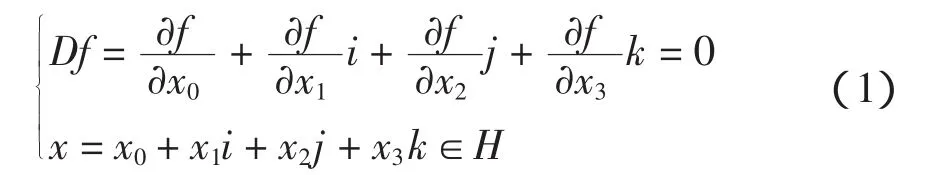
则称f是Ω上的左全纯函数。

由于本文不涉及右全纯函数，故在以下部分用全纯称呼左全纯。

不幸的是，最简单的非常值函数q却不满足式（1）从而不是全纯函数。为了弥补这一微分理论研究的缺陷，这里引入超复数，即所谓Fueter变量[5]如下：

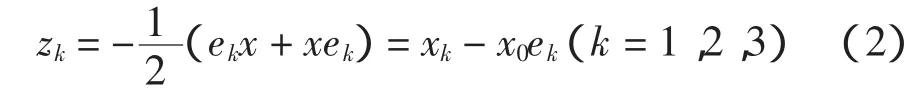
现在新的变元zk将满足条件Dzk=0。代入f的微分df中，因为dxk=dzk+dx0ek，故得到：

因此，f对x是全纯的当且仅当它的微分是超复变元微分的线性组合[5]。

在一般情形下，四元数多项式并不是全纯的。而且由于D（zizj）≠0（i，j=1，2，3，i≠j），超复变元的多项式也不一定是全纯的。

Delange[3]证明了Fueter多项式是全纯的。下面先给出：

定义1（Fueter多项式）设x∈H。对两个整数k1、k2，我们称k=（k1，k2）为一个双重指标。对指标的分量为非负时，记

k=|K|称为多重指标K的次数。

对一个至少有一个分量为负的多重指标，定义为：

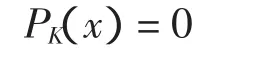
当次数k=0时，简单地写为K=（0，0）=0并且定义为：

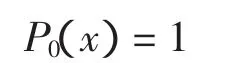
对于次数k＞0的K，我们定义Fueter多项式PK（x）如下：设K是多重指标j1，j2，…，jk，其中前k1个指标等于1而后k2个指标等于2.这时我们有记号

即这个积中恰好包含ki个zi，最后我们给出一般形式的Fueter多项式：

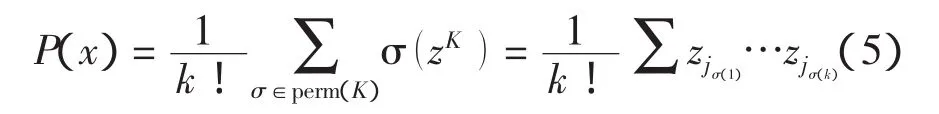
这里perm（k）是k个元素的置换群。式（5）中对称化的表达式弥补了H中的非交换性。

容易证明Fueter多项式是对H中的左作用和右作用都是线性不相关的[3]。与复分析一样，四元数函数也有用Fueter多项式给出的Taylor展开式。为此，引入函数

这是在原点有孤立奇点的最简单的全纯函数[3]。

对多重指标K=（k0，k1，k2，k3），记，现在定义函数

则用上述函数可展开Cauchy积分，从而得到下面定理。

定理2[3]设函数f在H中的开球|x|＜R上是全纯的，那么它可以展开成为一个收敛的Taylor级数：

特别地，如果f是全纯四元数多项式，则由定理1，它可以表示成Fueter多项式的和：

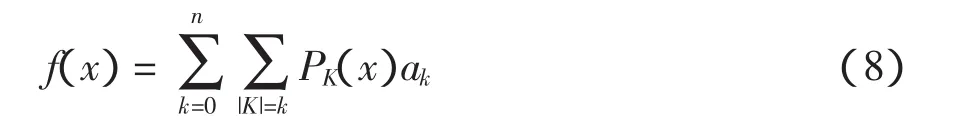
其中，n是f的阶数。

下面探讨多项式映射。

设F=（F1，…，Fn）：Cn→Cn为一个多项式映射，其个体形式为：

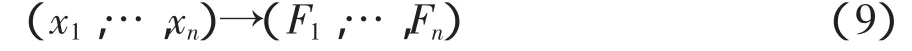
其中，Fi=Fi（x1，…，xn）是n元多项式。对w∈Cn，记JF为F的Jacobi矩阵，并记F′（w）=det（JF（w））n=2。著名的Jacobi猜想可组织为如下形式：

Jacobi猜想 设Fn：Cn→Cn是一个复多项式映射，对任意w∈Cn都有F′（w）≠0，则F是可逆映射，且其逆映射也是多项式映射。

Jacobi猜想首先由Keller对n=2时的整系数多项式映射提出。几十年过去了，许多数学家曾试图证明它，在产生了众多的错误证明后，直到今日它仍然是一个开问题[1，6]。但是在这些Jacobi猜想的证明过程中，产生了很多多项式和相关领域令人惊异的结果，下面的定理是其中最著名的一个。

定理3 如果对所有n≥2的正整数及deg（F）≤3的n元多项式映射F，Jacobi猜想都是成立的，则Jacobi猜想是正确（Bass，Connell，Wright[1]）。

本文仅讨论n=2情形的猜想。我们将揭示出Jacobi猜想和四元数分析的一些有趣对应。

设p（w）=（p1（w），p2（w））是二维复空间C2到其自身的多多项式映射，其中w=（w1，w2）∈C2。

我们知道四元数可以用两个复数来表示[5]：

令w1=x0+x1i，w2=x2+x3i，通过这个对应把C2和H等同起来，那么定义一个四元数函数如下：

注意w又可以用超复数来表示：

定理4 f（q）=f（z1，z2，z3）是q∈H的全纯函数。

证明：因为复多项式是复全纯函数，所以

及

由式（2）、（12）和（13）我们得到：

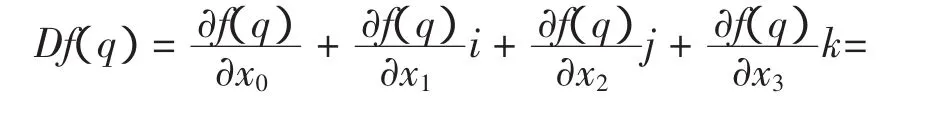
此即完成了定理证明。

简单计算显示f=f0+f1i+f2j+f3k，其中

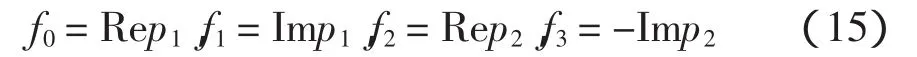
记Jf是四维实空间R4到其自身的映射f的Jacobi矩阵，那么由多复变函数论的熟知结论：

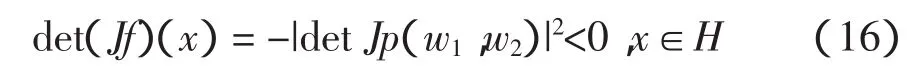
由文献[7]可知，Jacobi猜想成立当且仅当这个多项式映射是个单射。用K-代数的观点，如果这个映射是满射，猜想也是成立的[1]。因此为证明此猜想，我们仅需证明f（q）是H到H的满映射就足够了。而对任意q=ζ1+jζ2∈H（ζ1，ζ2∈C），令p1′=p1+ζ1，p2′=p2+ ζ2那么p′=（p1′，p2′）满足Jacobi猜想的条件。因此，如果我们能够证明对形如式（10）所定义的函数至少存在一个零点，则Jacobi猜想成立。

既然p（w）是从二维复空间到其自身的局部一对一映射，f（q）的可能零点只能是孤立的[4]。所以，自然可以考虑把复形式的Jacobi猜想推广到四元数全纯多函数，因为后者也是局部一一映射。

四元数Jacobi猜想如果f（q）是四元数H上的全纯多项式函数，且是非零的常值函数。则存在一个多项式H到H的全纯多项式映射g（q）使得g（f（q））f（g（q））=q即，f有多项式逆。

这个猜想从实质上推广了复形式的Jacobi猜想，这是因为确实存在不能表达为二元复多项式的组合的四元数全纯多项式。容易验证f=iz1+jz2+2kz3满足上面猜想的条件，但它不能有形如式（10）的表达式。而且，这里的猜想也是弱于已有反例的实形式的Jacobi猜想[6]。

［1］ BASS H，CONNELL E，WRIGHT D.The jacobian conjecture：reduction of degree and formal expansion of the inverse [J].Bulletin of the AMS，1982，7：287-330.

［2］ KOECHER M，REMMERT R，HAMILTON′s Q.GTM 123 [M].Berlin：Springer-Verlag，1990.

［3］ GUELEBECH K，HABETHA K，WOLFGANG S.Holomorphic Functions in the Plane and n-dimentional Spac[M]. Basel：Birkhuser，2008.

［4］ HEMPFLING T.Some remarks on zeroes of monogenic functions[J].Advances in Appl Clifford Algebras，2001，11（S2）：107-116.

［5］ MALONEK H R.Selected topics in hypercomplex function theory，Eriksson，Sirkka-liisa，Clifford algebras and potential theory[M].ProceedingsoftheSummerSchool，Mekrijrvi，2002.

［6］ PINCHUK S.A counterexample to the strong real Jacobian conjecture[J].Math Z，1994，217：1-4.

［7］ RUDING W.Injective polynomial maps are qutomorphisms [J].Amer Math Month，1995，102（6）：540-543.

Jacobian conjecture in quaternion form

LIU Hua，QU Fei-fei
（School of Science，Tianjin University of Technology and Education，Tianjin 300222）

The Jacobian conjecture in the view of hypercomplex analysis is elaborated in this paper.For a polynomial mapping P（w）=（p1（w），p2（w））：C2→C2the corresponding left holomorphic quaternionic polynomial f（z1，z2，z3）=p1（w）+jp2（w）is discussed：H→H，where w=（x0+x1i，x2+x3i）and z1=x1-x0i，z2=x2-x0i，z3=x3-x0i. then a new approach to the Jacobian conjecture is given by the use of argument from quaternionic holomorphic functions.

quaternionic analysis；holomorphic polynomial；Jacobian conjecture

book=2,ebook=78

O174.14

A

1673－1018（2010）02－0043－03

2010-01-08

刘 华（1971—），男，副教授，博士，硕士生导师，研究方向为复逼近论、解析边值问题等.