旋转机械故障诊断中的改进型RBF神经网络算法研究

张忠奎,王效岳,丁晓坤

(1.山东理工大学机械工程学院,山东 淄博 255049;2.聊城大学计算机科学学院,山东 聊城 252059)

旋转机械是石油、化工、冶金、机械等行业生产中的关键设备,随着其大型化、自动化、高速化和复杂化发展,运行的可靠性和安全性日益受到重视.因此,对其进行可靠、准确的故障诊断具有十分重要的意义.但是旋转机械结构的复杂性和耦合性又使得其故障具有多样性、模糊性和随机性等特点,因此很难用传统的模式分类技术将这些故障截然分开.而人工神经网络具有非线性模式分类性能和很强的自组织、自学习能力[1],不需要预先给出关于模式的先验知识和判别模型就能够通过自组织和自学习机制自动地形成所要求的决策域;同时,由于网络内部的非线性传递函数,使其对高维空间及非线性空间数据模式具有较强的分类能力,非常适用于设备的故障诊断.机械故障诊断中,常来用较为成熟的BP神经网络,但在实际的应用中,BP网络采用的是沿梯度下降的搜索求解算法,这就不可避免地存在网络学习收敛速度慢、易陷入局部极小、网络初值对学习性能影响比较大等缺陷[2].本文提出一种基于改进型RBF网络的旋转机械故障诊断方法,通过实际应用证明其学习速度和分类能力均优于BP网络.

1 改进型RBF神经网络

常规的RBF神经网络是具有单隐层的三层前馈网络,需先确定隐层节点个数,隐层节点一旦确定,网络结构也就固定,其拓朴结构如图1所示.RBF神经网络的学习是通过改变隐层节点基函数中心向量和隐层至输出层权值向量进行的.本文采用的改进型RBF神经网络模型是基于最近邻聚类学习算法的一种动态自适应RBF神经网络模型[3],它是一种在线自适应聚类学习算法,不需事先确定隐层单元个数,此算法可在线学习.用该算法构造网络的具体过程如下[4]:

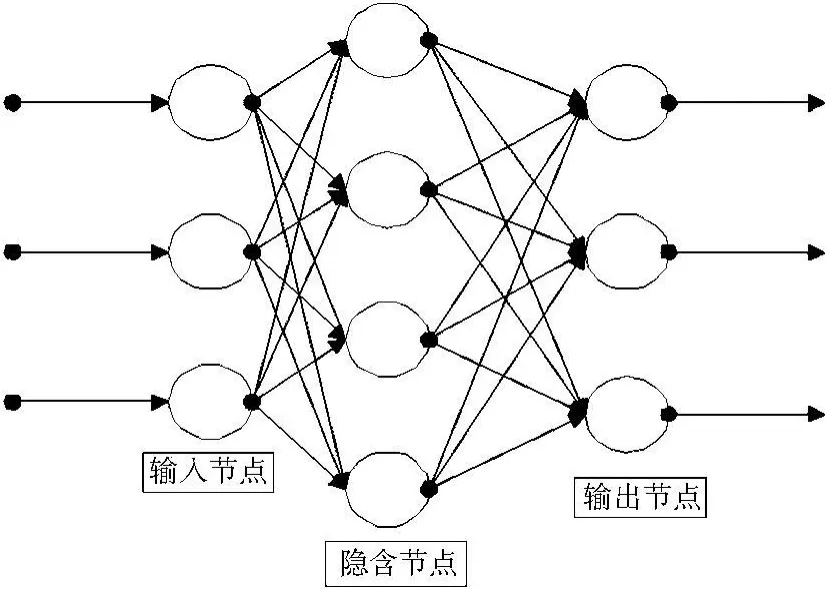
图1 RBF神经网络拓扑结构图

设有N对输入-输出数据对(xk,yk),k=1,2,…,N,RBF神经网络隐层非线性激励函数取高斯函数,RBF网络隐单元输出为

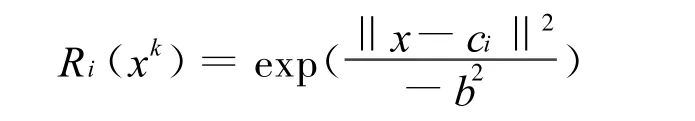
其中:xk是输入矢量;yk是输出:Ri(xk)是第i个隐单元的输出;ci是第i个隐单元高斯基函数的中心矢量;b是高斯基函数的半径.

1)定义S(l)用于存放属于各类的输出之和,定义计数器CT(l)用于统计属于各类的样本个数,其中l为类别数,选择一个半径b.

2)从第一个样本对(x1,y1)开始,在x1上建立一个聚类中心,令c1=x1,S(1)=y1,CT(1)=1.这样建立的RBF网络只有一个隐单元,该隐单元的中心为c1,该隐单元到输出层的权值为W1=S(1)/CT(1).

3)假设考虑第k个样本数据对(xk,yk)时,k=3,4,…,N,设已存在n个聚类中心,其中心点分别为c1,c2,…,cn,网络中已有n个隐单元.分别求出xk到这n个聚类中心的距离|xk-ci|,i=1,2,…,n,设|xk-cj|为这些距离中的最小距离,即cj为xk的最近邻聚类,则:

如果|xk-ci|＞b,则将xk作为一个新聚类中心,并令cn+1=xk,S(n+1)=yk,CT(n+1)=1,且保持S(i),CT(i)的值不变.在上述建立的RBF网络中再添加第n+1个隐单元,该隐单元到输出层的权矢量为Wn+1=S(i)/CT(i).

如果|xk-ci|≤b,则S(j)=S(j)+yk,CT(j)=CT(j)+1.隐层到输出层的权矢量为Wi=S(i)/CT(i).

4)根据上述规则建立的动态RBF神经网络输出为

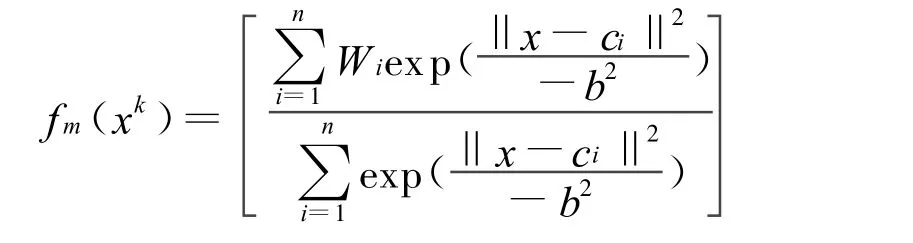
由网络结构的构造过程可见:高斯基函数半径的大小决定了网络的复杂程度.b越小,所得到的聚类数目就越多,从而导致非线性回归过程越复杂,计算量也越大.但b是一个一维参数,一般可以通过实验和误差信息找到一个适当的值;由于每一个输入-输出数据对都可能产生一个新的聚类,因此构造出的网络是一种动态网络,实际上同时在进行参数和结构两个过程的自适应调整.

2 改进型RBF神经网络在旋转机械故障诊断中的应用

2.1 学习样本的建立

频域转子发生故障时的重要特征是机器伴有异常的振动和噪声.振动信号对机器设备的运行状态有直接的反映.尤其在频域内,特征频段上特征量的大小和比例关系可以反映出相应的故障类型.在BENT LY RK-4模拟转子试验台上进行实验研究,从测振传感器提取出的时域连续振动信号,经A/D转换、DFT(FF T)分析,得到振动信号的频谱分析.本文以旋转机械中常见的质量不平衡、转子热弯曲、轴向碰磨等8种故障作为网络输出,利用振动信号频谱中的7个频段上的不同频率的谱峰能量值作为特征量,形成训练样本和样本的目标输出(见表1,表1中f为转子的工作频率).样本的目标输出中,1表示对应故障发生,0表示对应故障不发生.

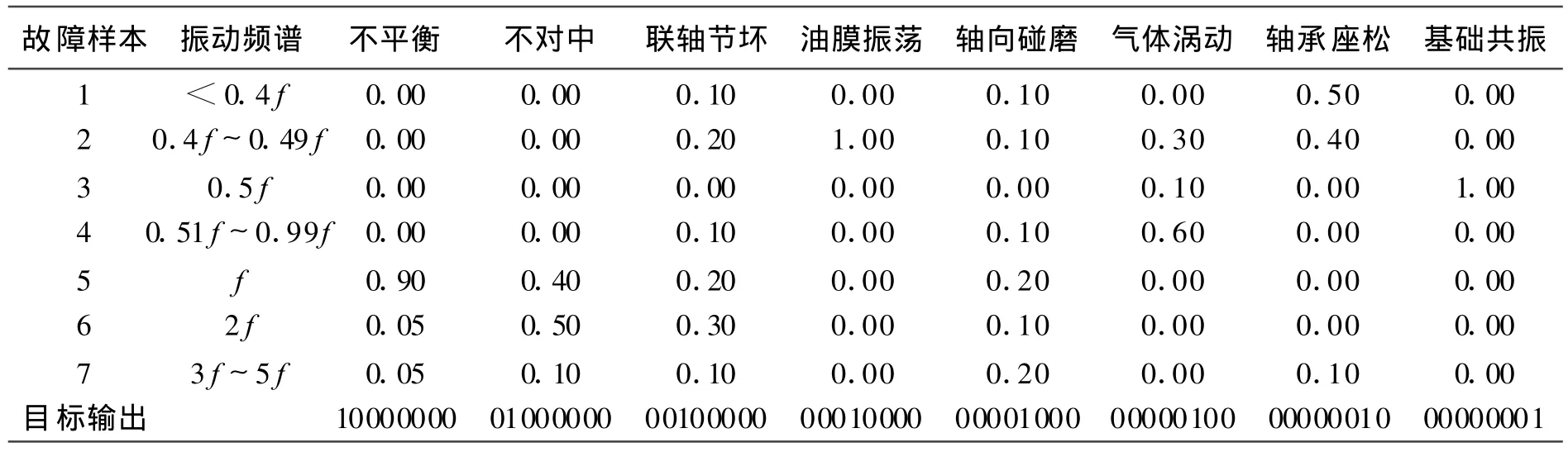
表1 旋转机械常见故障标准模式特征向量

2.2 网络结构的选取

由表1所列的学习样本可知,输入层选取7个节点;输出层为综合评价层,选择了8个输出层节点.

2.3 网络学习性能分析

用表1所示学习样本分别对具有相同结构的BP网络和改进的RBF网络进行训练,训练结果见表2.由表2可以看出,标准BP算法学习过程比较缓慢,而采用RBF网络则学习过程非常快.

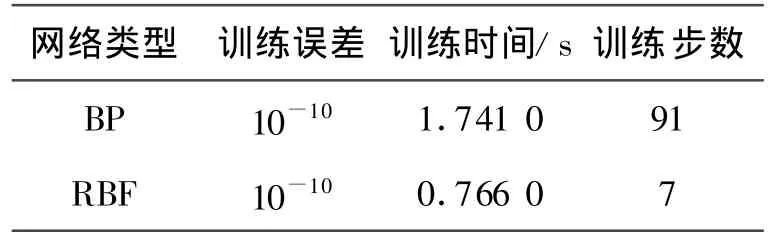
表2 网络学习性能比较

2.4 网络的测试

将待识别的故障样本(见表3)作为网络的输入,输入到上面已经训练好的网络中,经网络非线性映射的输出结果见表4.从表4可以看出,4个故障输入模式分别对应第2、5、7、4个输出节点的输出值,分别接近于1,其它节点的输出值均未超过0.3,可以分别诊断为不对中、轴向碰磨、轴承座松和油膜振荡故障.可见网络对待识别样本进行了正确的分类,测试结果与实际发生的故障吻合.

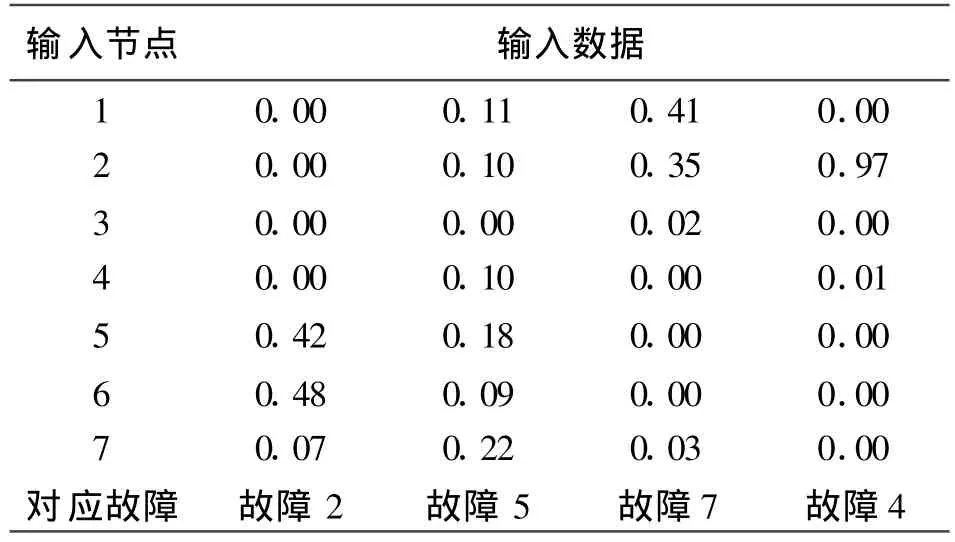
表3 待检测故障模式特征向量

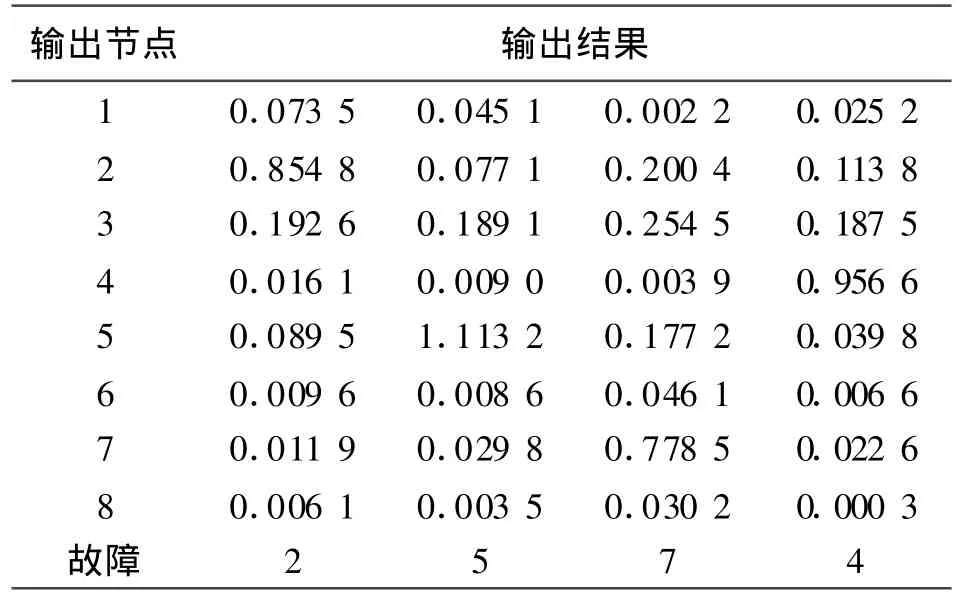
表4 网络诊断结果

3 结束语

与目前广泛应用的BP算法相比,改进型网络学习算法从根本上避免了陷入局部极小点的问题,并且RBF网络训练速度非常快.旋转机械故障诊断中的实际应用表明,改进型网络能够对旋转机械各种复杂状态做出判断,具有良好的实用性.

[1]王伟.人工神经网络——入门与应用[M].北京:北京航空航天大学出版社,1995.

[2]苏高利.基于Matlab语言的BP神经网络的改进算法[J].科技通报,2003,19(2):130-135.

[3]王立新.自适应模糊系统与控制——设计与稳定性分析[M].北京:国防工业大学出版社,1995.

[4]朱明星,张德龙.RBF网络基函数中心选取算法的研究[J].安徽大学学报,2000,24(1):72-78.