正矩阵谱半径及其特征向量的新算法

徐强，宋海洲，田朝薇

（华侨大学数学科学学院，福建 泉州 362021）

正矩阵谱半径及其特征向量的新算法

徐强，宋海洲，田朝薇

（华侨大学数学科学学院，福建 泉州 362021）

设计一种计算正矩阵谱半径及其特征向量的新算法，并证明算法的收敛性.结果表明，算法具有计算量小，便于实现，且能较快达到所需精度的特点.数值试验进一步验证了其可行性.

正矩阵；谱半径；特征向量；收敛性

正矩阵的谱半径在数值分析、图论、计算机科学、管理科学等领域中有着重要的作用，因此，对正矩阵谱半径的计算一直都是研究的重点［1-4］.通常计算正矩阵的谱半径都是采用幂法［1］，但幂法的计算量相对较大.本文设计了一种计算正矩阵谱半径及其特征向量的新算法，并证明了该算法的收敛性.

1 算法的设计

2 算法收敛性及收敛速度

已知正矩阵C，先对其谱半径进行上、下界估计.

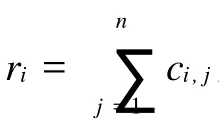
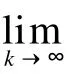
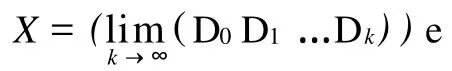
3 数值试验

表1 数值试验结果表Tab.1 Table of mumerical experiment result

［1］蒋正新，施国梁.矩阵理论及其应用［M］.北京：北京航空学院出版社，1988：359.

［2］章伟，黄廷祝.不可约M-矩阵最小特征值的估计［J］.工程数学学报，2004，21（8）：31-34.

［3］段复建，张可村.Z-矩阵最小特征值及特征向量的数值算法［J］.工程数学学报，2007，24（3）：563-566.

［4］徐成贤，徐宗本.矩阵分析［M］.西安：西北工业大学出版社，1991：270-309.

［5］宋海洲.关于合同变换矩阵的一般形式［J］.华侨大学学报：自然科学版，2004，25（2）：130-132.

A New Algorithm for the Spectral Radius and Its Eigenvector of Positive Matrix

XU Qiang，SONG Hai-zhou，TIAN Zhao-wei
（School of Mathematical Sciences，Huaqiao University，Quanzhou 362021，China）

A new algorithm for the spectralradius and its eigenvector of positive matrix is designed，and the convergence of the algorithm for this algorithm is also proved.The results show that the algorithm has the characteristic of small calculate amounts，easy to achieve，and can reach the required precision rapidly.The feasibility of the algorithm is also proved by numerical experiment.

positive matrix；spectralradius；eigenvector；convergence

O 151.21

A

1000-5013（2010）04-0473-03

（责任编辑：陈志贤 英文审校：张金顺，黄心中）

2008-06-19

宋海州（1971-），男，副教授，主要从事数学模型及运筹学的研究.E-mail：hzsong@hqu.edu.cn.

福建省自然科学基金资助项目（Z0511028）