可加布朗运动增量“快点”集的Packing维数
邱志平,林火南
(1.华侨大学数学科学学院,福建 泉州 362021;2.福建师范大学数学与计算机科学学院,福建 福州 350007)
可加布朗运动增量“快点”集的Packing维数
邱志平1,林火南2
(1.华侨大学数学科学学院,福建 泉州 362021;2.福建师范大学数学与计算机科学学院,福建 福州 350007)
讨论可加布朗运动样本轨道的重分形分析问题.利用构造上极限型集,集的乘积的Packing维数和Hausdorff维数关系的方法,分别得到其局部增量和沿坐标方向增量两种不同增量形式“快点”集的Packing维数结果.
可加布朗运动;“快点”集;Packing维数;重分形分析
1 预备知识
Orey等[1]在讨论布朗运动的重对数律时,得到了布朗运动增量“快点”集的Hausdorff维数结果.在多指标随机过程研究中,Wiener单是最具重要性和代表性.在讨论Wiener单的样本轨道性质中,可加布朗运动起到关键的作用[2-5],但是,可加布朗运动是可加Lévy过程(Additive Lévy Processes)的特例,是源自Lévy过程的相交与自相交问题[6].可加Lévy过程是指满足

条件的多指标随机过程,即

其中,Xi={Xi(t)∶t∈R+}(1≤i≤N)是取值于Rd相互独立的Lévy过程.若Xi(1≤i≤N)均为布朗运动,则称X={X(t)∶t}为可加布朗运动.

而沿坐标方向增量“α-快点”集记为

文[7]得到了AT(α)与BT(α)Hausdorff维数结果,当T>0,0≤α≤时,则dim(AT(α))=N-α2,a.s.(即几乎处处,下略);而当T>0,0≤α≤1时,则 dim(BT(α))=N-α2,a.s..
定理1 设T>0,0≤α<1,AT(α)如式(1)所示,则dim(AT(α))=N,a.s..
定理2 设T>0,0≤α<1,BT(α)如式(2)所示,则dim(BT(α))=N,a.s..
由此可发现,当0<α<1时,AT(α)和BT(α)的Hausdorff维数与其Packing维数不相等.
2 基本引理


则φ-p(E)是一个测度,称φ-p(E)为E的Packing测度.定义E的Packing维数为
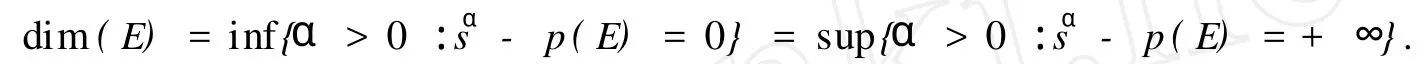
有关Packing测度和Packing维数的有关性质,可参见文[8].
设Bi={Bi(ti)∶ti∈R+}(1≤i≤N),是定义在(Ω,F,P)上的标准布朗运动,它们相互独立,若


3 主要结果及其证明
下面,给出可加布朗运动局部增量“快点”集的Packing维数.
定理3 设T>0,0≤α0<1,AT(α0)如式(1)所示,则dim(AT(α0))=N,a.s..
证明 仅对N=2的情况结予证明,N>2的情况类似可得.不妨假设T=1,α1∈(α0,1),δn=n2-n(n≥1).定义一族服从(0-1)分布的随机变量序列{ZI}I∈Mn(n≥1)如下:
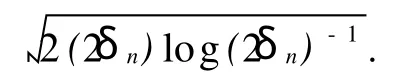
由布朗运动一致连续模结果[1]可知,几乎处处(a.s.)地存在n0=n0(ω),使得当n≥n0(ω)时,对于∀I∈Mn,∀s∈I,有

若进一步地,ZI=1,当n充分大之后,则有



定理4 设T>0,0≤α0<1,BT(α0)如式(2)所示,则dim(BT(α0))=N,a.s..
证明 仅对N=2的情况给予证明,N>2的情况类似可得.由于

对于∀E,F⊆Rd[10],有
dim(E)+dim(F)≤dim(E×F)≤dim(E)+dim(F).


[1]OREY S,TAYLOR S J.How often on a Brownian path does the law of iterated logarithm fail?[J].Proc London Math Soc,1974,28(1):174-192.
[2]黄群,林火南.布朗单样本轨道的重分形分析[J].福建师范大学学报:自然科学版,2003,19(2):1-8.
[3]EHM W.Sample function properties of mutli-parameter stable processes[J].Probability Theory and Related Fields,1981,56(2):195-228.
[4]林火南.Wiener单的局部时和水平集的Hausdorff测度[J].中国科学:A辑,2000,30(10):869-880.
[5]KHOSHNEVISAN D,SHI Z.Brownian sheet and capacity[J].Ann Probab,1999,27(3):1135-1159.
[6]KHOSHNEVISAN D,XIAO Y M.Level sets of additive Lévy processes[J].Ann Probab,2002,30(1):62-100.
[7]邱志平,林火南.可加布朗运动样本轨道的重分形分析[J].福建师范大学学报:自然科学版,2004,20(4):14-19.
[8]FALCONER KJ.Fractal geometry-mathematical foundations and application[M].New York:John Wiley,1990.
[9]DEMBO A,PERES Y,ROSEN J,et al.Thick points for spatial Brownian motion:Multifractal analysis of occupation measure[J].Ann Probab,2000,28(1):1-35.
[10]TRICOT C.Two definitions of fractal dimension[J].Math Proc Cambridge Philos Soc,1982,91(1):57-74.
[11]XIAO Yi-min.Packing dimension,Hausdorff dimension and Cartesian product sets[J].Math Proc Cambridge Philos Soc,1996,120(3):535-546.
Packing Dimension of“Fast Point”Sets for Additive Brownian Motion
QIU Zhi-ping1,LIN Huo-nan2
(1.School of Mathematical Sciences,Huaqiao University,Quanzhou 362021,China;2.School of Mathematics and Computer Science,Fujian Normal University,Fuzhou 350007,China)
The multifractal analysis for the sample paths of additive Brownian motion is discussed in this paper.The Packing dimension of“fast point”sets determined by the local increment and by the incerment in the direction of coordinate for additive Brownian motion are obtained respectively by means of constructing a limsup random set and the relation between Packing dimension and Hausdorff dimension of the Product sets.
additive Brownian motion;“fast point”sets;Packing dimension;multifractal analysis
O 211.6
A
1000-5013(2010)04-0480-03
(责任编辑:陈志贤 英文审校:张金顺,黄心中)
2008-09-24
邱志平(1979-),男,讲师,主要从事随机过程理论及应用的研究.E-mail:qzp@hqu.edu.cn.
华侨大学科研基金资助项目(08HZR20)
——陈桂蓉教授

