一类广义Fibonacci数列的研究

陈淑贞

（海南师范大学 数学与统计学院，海南 海口 571158）

一类广义Fibonacci数列的研究

陈淑贞

（海南师范大学 数学与统计学院，海南 海口 571158）

著名的Fibonacci数列有许多通项表达式和性质.本文研究了当u=v=2，R0=a，R1=b时的广义Fibonacci数列{Rn}，利用特征方程的特征根得到了它的通项公式，还推出了几个求和公式.

广义Fibonacci数列；通项；求和公式

1 引言和定义

十三世纪意大利著名数学家斐波那契（Fibonacci）提出了一个有趣的关于兔子繁殖的问题，从而引出了一个有趣的数列—Fibonacci数列［1］，记为{Fn}，它是满足Fn+1=Fn+Fn-1，F1=F0=1的数列，这个数列的每一项称为Fibonacci数，人们对这个数列的研究兴趣历时几百年而不衰，现在已得出它的许多通项表达式和性质，在计算数学、优化理论、运筹学等领域有着广泛的应用.后来人们又将这个数列进行推广，得到了广义Fibonacci数列［1］，关于广义Fibonacci数列，已有不少的研究成果［2-10］，文献[2]和[3]分别利用生成函数、数学归纳法和特征方程的特征根求出了广义Fibonacci数列的三个通项表达式.本文继续对这类数列进行了研究.

定义1［1］若数列{Rn}满足

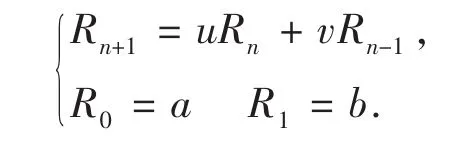
其中 a，b，u，v∈R，称该数列{Rn}为广义 Fibonacci数列.

定义2［6］方程x2-ux-v=0称为递推关系Rn+1=uRn+vRn-1的特征方程，它的根称为特征根.

定义3 当u=v=2，R0=a，R1=b时的广义Fibonacci数列{Rn}称为2-2型广义Fibonacci数列.

本文主要研究了2-2型的广义Fibonacci数列{Rn}，利用递推关系的特征方程的特征根获得它的一个通项公式，同时还推导出几个求和公式.

2 通项公式

定理 {Rn}为2-2型广义Fibonacci数列，则{Rn}的通项为

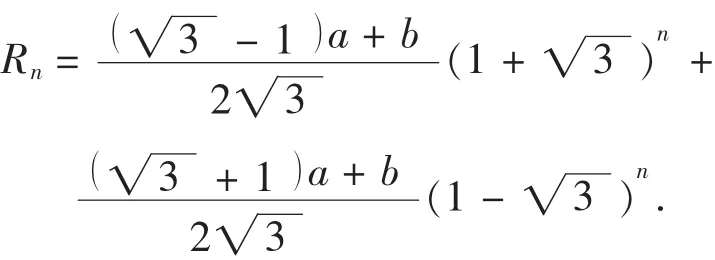
证明 因为{Rn}满足递推关系

3 求和公式

数列求和是研究数列性质的一个重要内容.下面推出几个2-2型广义Fibonacci数列的求和公式.

证明 因为

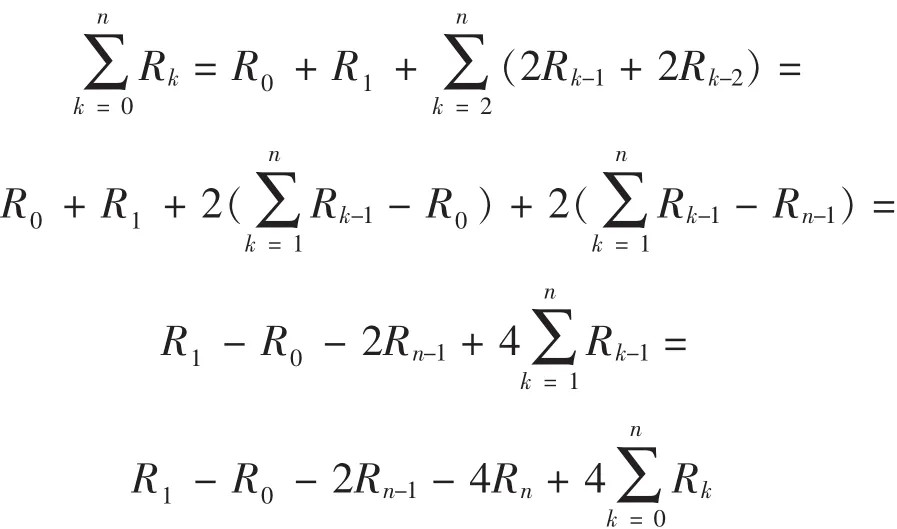
所以有

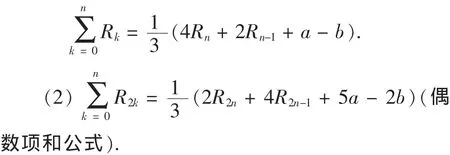
证明 因为

证明 因为

证明 当m=2n时，

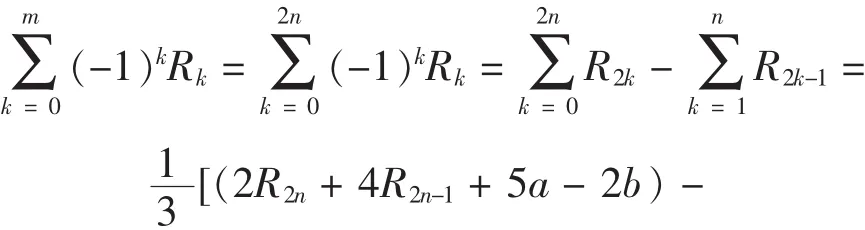
（2R2n-2R2n-1-4a+b）]=2R2n-1+3a-b.所以，等式成立.

当m=2n+1时，

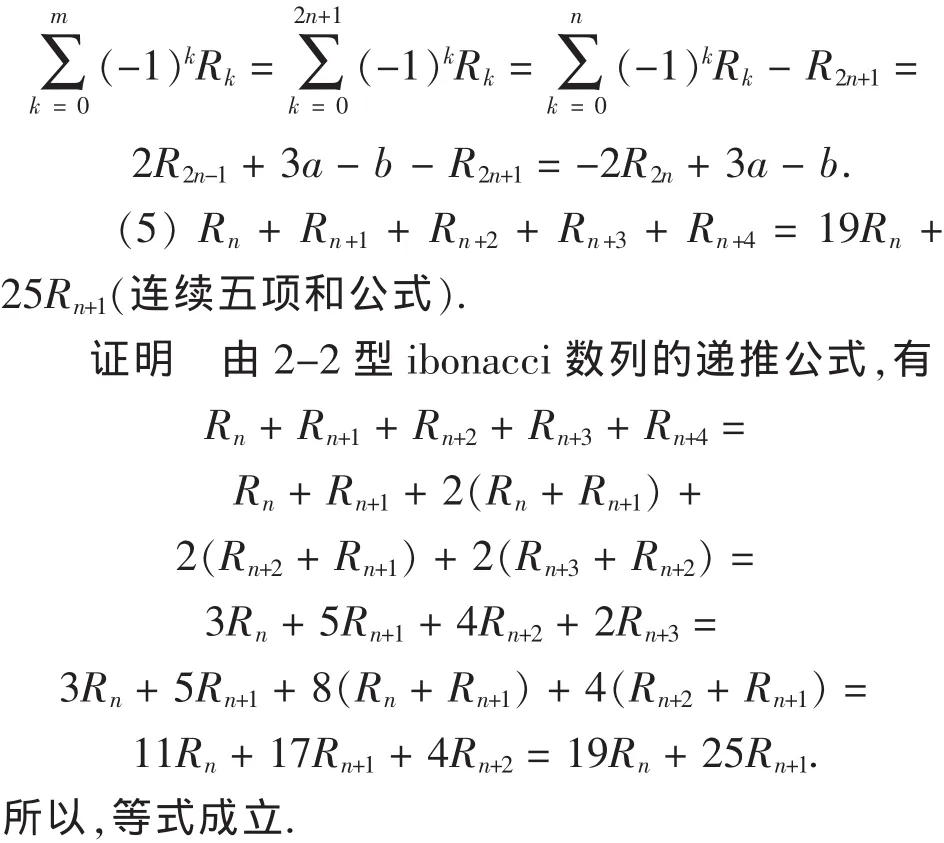
［2］马巧云.广义Fibonacci数列的通项[J].西安联合大学学报，2004，7（5）：30-32.

［3］陈淑贞，曾庆年.广义Fibonacci数列的通项及性质[J].海军工程大学学报，2008，20（3）：11-14.

［4］邵品综.广义Fibonacci序列及其应用[J].青岛教育学院学报，2001，14（1）：36-43.

［5］张纪平.一类广义斐波那契数列及其应用[J].泉州师范学院学报，2005，23（2）：10-13.

［6］孙淑玲，许胤龙.组合数学引论[M].合肥：中国科学技术大学出版社，2005.

［7］陈淑贞，鲁仲池.四阶Fibonacci数列的通项和性质[J].海军工程大学学报，2009，21（1）：35-40.

［8］李海青.两类广义Fibonacci数列的关系[J].青海师范大学学报：自然科学版，2002，（3）：24-25.

［9］吴茂念.广义Fibonacci数列一些前n项和式[J].贵州大学学报：自然科学版，2005，22（4）：343-347.

［10］朱伟义.广义Fibonacci数的几个组合恒等式 [J].浙江师范大学学报：自然科学版，2007，30（1）39-42.

［1］吴振奎.世界数学名题欣赏—斐波那契数列 [M].沈阳：辽宁教育出版社，1995.

责任编辑：毕和平

Study on a Kind of Generalized Fibonacci Sequence

CHEN Shuzhen（College of Mathematics and Statistics，Hainan Normal University，Haikou 571158，China）

There are many general expressions for famous Fibonacci sequence.In this paper，We study a kind of generalized Fibonacci sequence while u=v=2，R0=a，R1=b.By using eigen roots of it's eigen equation，we obtain its general expression.We also derive some summation formula.

generalized Fibonacci sequence；general expression；summation formula

O 157

A

1674-4942（2010）01-0001-03

2009-12-07

海南师范大学应用数学重点学科基金资助项目