一种大安装角条件下的传递对准算法研究
孙 茜 刘建业 曾庆化
(南京航空航天大学自动化学院,南京 210016)
瞄准吊舱是一种安装在军用飞机上的目标指认系统,用于定位目标,并引导精确制导武器打击目标.瞄准吊舱中置有IMU惯性器件,用以精确测定吊舱的姿态,形成控制信号,使吊舱传感器始终稳定指向目标,提供对目标的跟踪和锁定能力.快速精确地对吊舱姿态进行初始对准是瞄准吊舱中的一项关键技术,也是近年来惯性技术领域研究的重要课题之一[1-2].
在传递对准方法中,有位置匹配、速度匹配、角速率匹配等多种信息匹配方式.由于由相对失准角产生一定数量位置差值的时间长,所以位置匹配常作为辅助方法;速度匹配用得最早,也最为成熟,但由于速度信息不能直接从测量元件得到,计算量大、时间长;之后提出的角速率匹配对准方法能获得较好的对准效果,但受陀螺漂移的影响较大[3].文献[4]提出了基于“比力积分匹配”方式的动基座传递对准,在载体低速机动的条件下,避免了陀螺漂移的影响,有效提高了中低精度捷联惯导系统的传递对准的快速性和准确性.
实际情况下,吊舱安装在机腹下通常有一个固定安装角.现假设吊舱惯导系统与飞机机腹有一固定大小(15°左右)的俯仰安装角.吊舱安装时,在此15°固定安装角的基础上会有较小的安装误差角,通常在5°以内.若将安装角和安装误差角之和作为卡尔曼滤波的状态估计量,直接利用文献[4]的“比力差积分匹配”传递对准算法.此时建立的状态方程不再是线性模型,不能直接利用卡尔曼滤波器进行估计,需要寻求新的滤波方法,这种解决方法扩大了原问题的复杂度,本文提出了一种简单易行的方法,基于文献[4]的算法,在不改变原状态方程和观测方程的基础上,提出了一种对子惯导数据进行预处理的改进型“比力积分匹配”传递对准算法.该算法不直接利用子惯导数据,而是将子惯导数据转换到过渡坐标系后进行卡尔曼滤波,再将滤波结果转回到子惯导坐标系,获得子惯导实时的姿态信息.仿真结果证明,该方法有效解决了大安装角下的传递对准问题,具有工程参考价值.
1 比力积分传递对准
传递对准技术的基本原理是:以已对准的机载高精度惯导系统(又称主惯导系统)的导航坐标系为基准,估计出低精度惯导系统(又称子惯导系统)所对应的载体坐标系bs相对导航坐标系的姿态矩阵.传递对准利用主惯导的姿态信号构成姿态矩阵,将其输入子惯导的导航计算机.在理想情况下,主、子惯导姿态矩阵应相同,即,但在实际传递对准中,由于存在3种误差源(主惯导平台误差角φ[5]、导弹在机翼上的安装误差角ζ和机翼弹性变形失调角ρ),使子惯导的数学平台n′s系相对理想导航坐标系存在误差角 φss,即

将φss分解到x,y,z坐标轴,则子惯导到主惯导坐标系之间的转换矩阵为
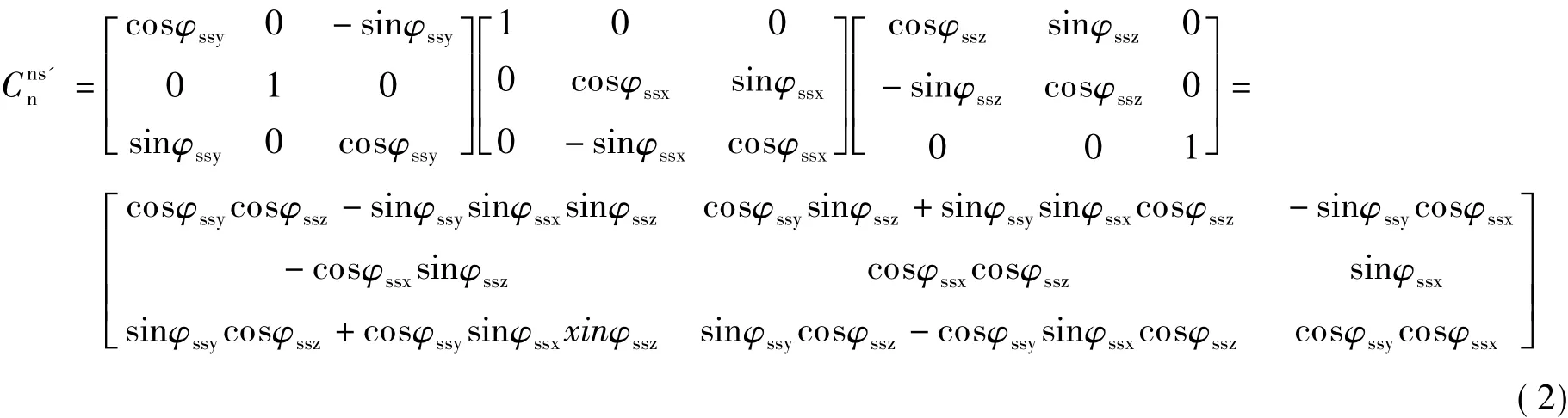
子惯导的姿态阵为

当 φss<5°时,有 sinφssx≈φssx,cosφssx≈φssx,忽略微量的乘积,化简式(2)有
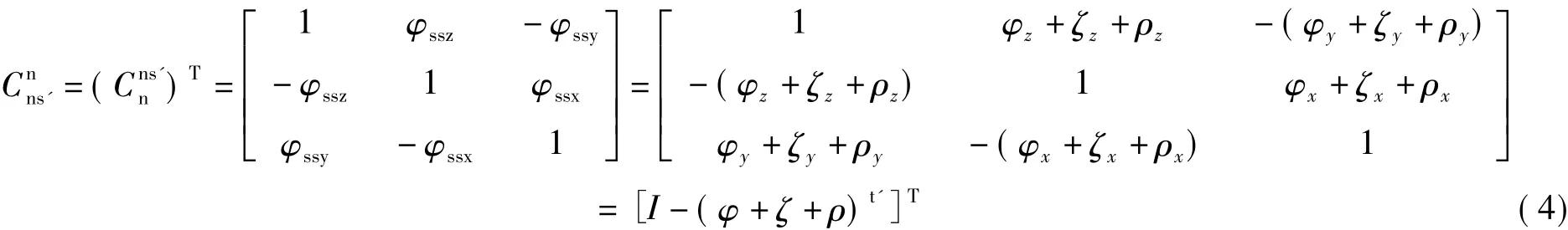
其中,
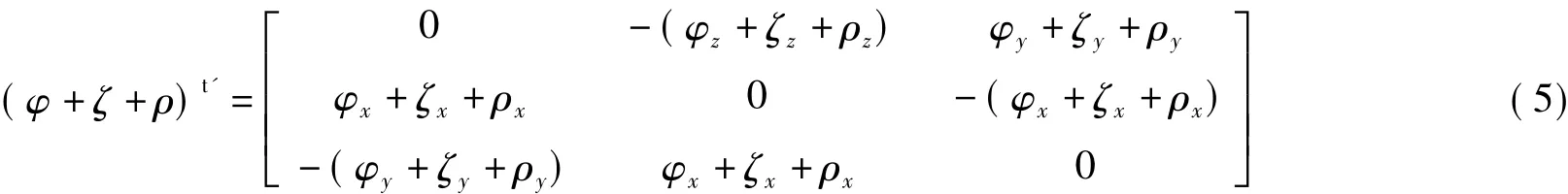
“比力积分匹配”传递对准数学模型由主/子惯导速度误差、主/子惯导平台误差角、机翼挠曲变形角、陀螺随机漂移之差、加速度计零位随机偏置之差等动态方程组成,考虑传递对准时间极短,所以Master-INS/Slave-INS的陀螺漂移和加速度零位随机偏置均可看作随机常数[6].联合传递对准状态方程和观测方程,通过卡尔曼滤波器即可对该传递对准过程中的状态量进行最优滤波估计,从而精确估算出主/子惯导之间的误差角,实现传递对准.卡尔曼滤波模型见文献[4].
主、子惯导间的绝对准线速度误差值δV是观测系统观测的重要状态矢量之一,所以必须准确地描述比力积分误差δV的动态运动方程.将比力差方程[4]展开得

在基于主子惯导“比力积分匹配”的传递对准方法中,式(6)成立的前提是误差角为小量(<5°),而在现在的条件下,俯仰误差角已经达到了15°,不能再利用式(4)建立比力差状态方程和观测方程,一种比较容易想到的解决方案是回归到精确表达式(2)重新建立状态方程和观测方程,但是此方法建立的新模型是非线性模型,不能利用卡尔曼滤波器进行状态估计.显然,这种解决方案扩大了问题本身的复杂度,本文提出的解决方案不改变原状态方程,并且能有效利用卡尔曼滤波器.
2 改进算法及仿真验证
考虑仍利用现有的误差模型进行对准,则需要采用预处理的方法将大角度情况转换为“小角度情况”.具体方案如下:引入子惯导过渡坐标系——此坐标系修正了15°的固定安装俯仰角,与主惯导之间的安装误差角为小角度.此时利用线性误差模型进行传递对准,对准后得到子惯导过渡姿态,对其再次进行俯仰角回转修正,得到实际的子惯导姿态.
应用到仿真程序中,由于在“比力积分匹配”传递对准中,仅用到比力信息,所以对子惯导比力进行坐标系转换即可.转换方法为:在子惯导比力信息乘以绕俯仰轴转动的姿态转换矩阵[7],即可得到过渡坐标系下的比力输出,

采用此方法对子惯导比力信息进行转换(取θ=15°),同时与理想值进行比较,对比结果如图1所示.可见,转换前的比力值由于15°的俯仰角误差影响,距离主惯导参考值(理想值)较远,而经过坐标转换后的比力值与理想值非常接近,也就是说,经过比力转换,原大角度情况转化为小角度,建立的线性模型仍然适用.
利用该方法进行“比力积分匹配”传递对准后,得到子惯导在过渡系中的姿态信息,再将此姿态信息回转修正到真实坐标系(俯仰角回转15°),即可得到子惯导当前时刻的实际信息.下面进行仿真验证.
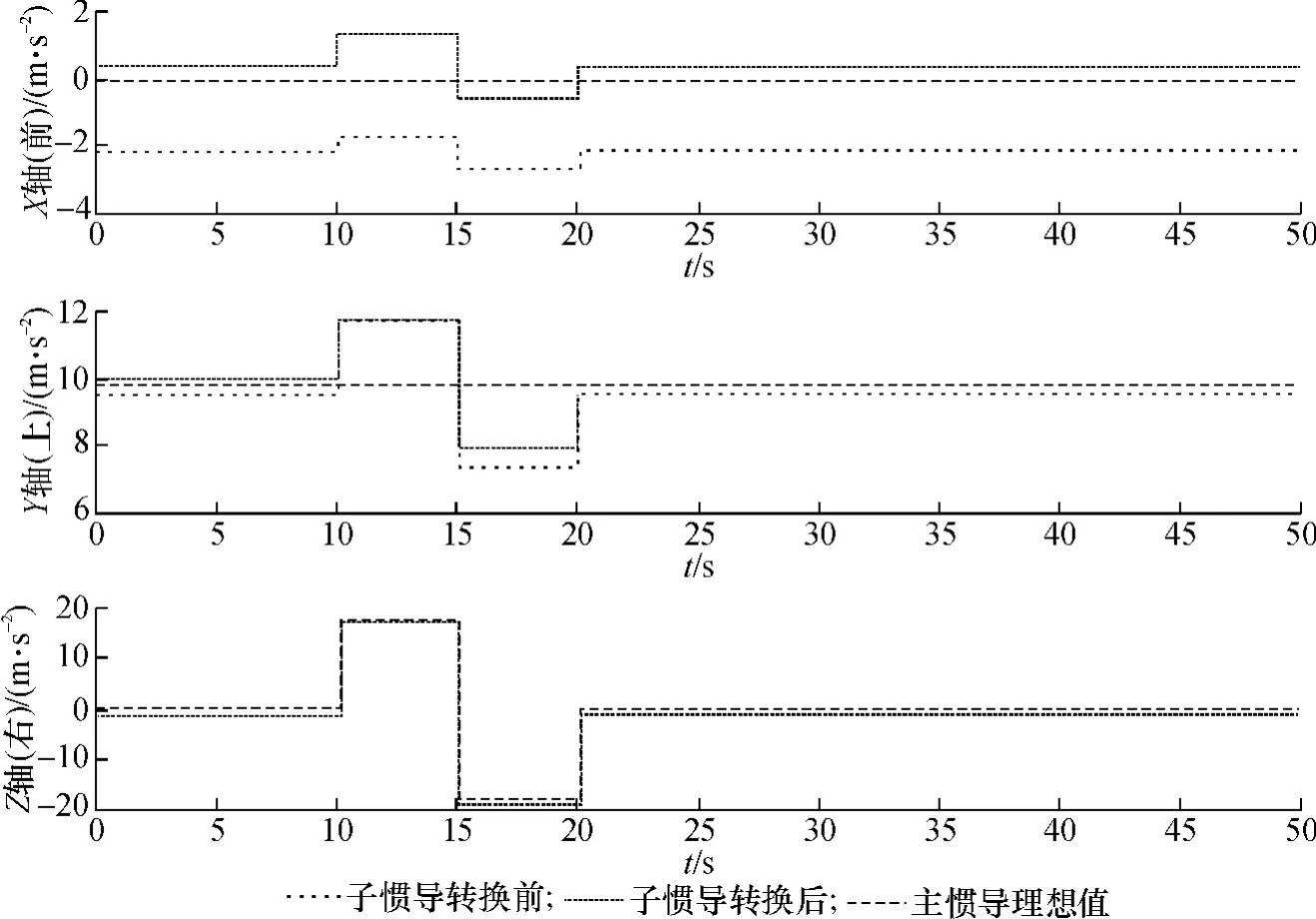
图1 比力转换对比图
仿真条件设置如下:
1)瞄准吊舱偏离飞机中心距离为0.5 m(纵向)、0.5 m(垂直)、1.5 m(翼展);瞄准吊舱平台误差角分别为 3.0°,2.0°,3.0°;挠曲变形角一阶马尔可夫过程噪声为 0.2°,相关频率为 2/s;
2)主惯导精度远高于子惯导,其器件误差忽略不计,子惯导陀螺随机漂移常值1.0(°)/h,随机漂移白噪声1.0(°)/h,加速度计零位随机常值10-4g,加速度计马尔可夫零偏10-4g;
3)误差状态量初始值均为0;初始估值误差协方差阵P0/0对角线元素分别为(2 m/s)2,(2 m/s)2,(2 m/s)2,(0.3°)2,(0.3°)2,(0.3°)2,(0.3°)2,(0.3°)2,(0.3°)2,(1°/h)2,(1°/h)2,(1°/h)2,(1 ×10-3g),(1 ×10-3g),(1 ×10-3g);
4) 初始位置:经度 106.5°,纬度 29.5°,高度 300.0 m;初始姿态:横滚 0.0°,俯仰 0.0°,航向 30.0°;初始速度200 m/s,向前飞行;
5)由于在“比力积分匹配”传递对准下,载体直线飞行时方位失准角不可观,因此必须使载体进行方位机动,即产生横向加速度,才能使方位失准角可观[8].设置蛇形(S形)机动时间为10 s,转弯角速度为5(°)/s.
基于上述仿真参数,进行主惯导数据延时传递对准仿真,仿真流程框图如图2所示,子惯导姿态精度改进前后的结果如图3所示.

图2 改进法传递对准仿真流程框图
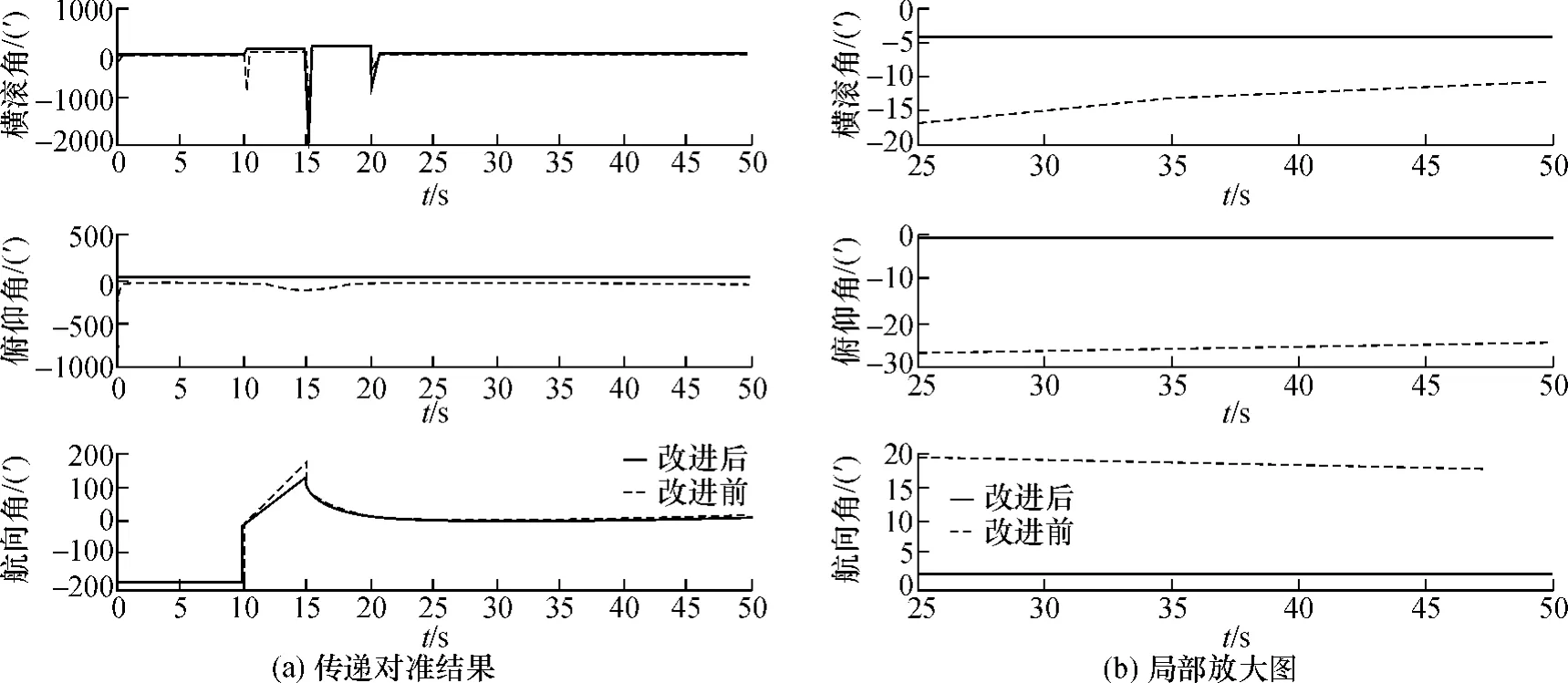
图3 改进前后子惯导姿态精度比较
分析可知,卡尔曼滤波器估计出的子惯导的实际姿态与理想姿态存在较大的误差:横滚角10′,俯仰角25′,航向角18′(见表1).这样的精度无法达到对准指标要求,经过预处理和回转修正后的姿态精度得到了较大的提高:横滚角4′,俯仰角2.5′,航向角2′.该精度范围达到了高精度传递对准指标的要求,具有实际应用意义.

表1 改进方案传递对准结果前后对比
3 结语
本文针对大安装角的实际情况,基于“比力积分匹配”传递对准算法,提出了一种基于坐标转换预处理的改进算法,将子惯导比力值通过旋转转换到过渡坐标系,利用线性误差模型进行传递对准,再将对准结果回转到真实坐标系,得到子惯导真实姿态信息.在上述大安装俯仰角情况下,经过本文的转换方法,子惯导比力得到修正,用转换后比力进行传递对准,横滚角对准精度在4′左右,航向角和俯仰角对准精度在3′左右.仿真结果表明,坐标转换预处理方法有效地解决了大安装角情况下的传递对准问题,分析可知,该方法具有一定的通用性和重要的工程应用价值.
References)
[1]Cur R K,Ash M E,Thielman L O,et al.Proposed IEEE inertial systems terminology standard and other inertial sensor standards[C]//IEEE Position Location Navigation Symposium.Monterey,CA,USA:IEEE,2004:83-90.
[2]宫晓琳,房建成,郭雷.SINS快速精确传递对准技术研究[J].宇航学报,2008,29(4):1228-1232.Gong Xiaolin,Fang Jiancheng,Guo Lei.Research on SINS rapid transfer alignment technology[J].Journal of Astronautics,2008,29(4):1228-1232.(in Chinese)
[3] Noureldin Aboelmagd,Shin Eun-Hwan.Improving the performance of alignment processes of inertial measurement units utilizing adaptive pre-filtering ethodology[C]//ION 58th Annual Meeting/CIGTF 21st Guidance Test Symposium.Albuquerque,New Mexico,2002:24-26.
[4]钱伟行.捷联惯导与组合导航系统高精度初始对准技术研究[D].南京:南京航空航天大学,2010.
[5] Gao Wei,Ben Yueyang,Sun Feng,et al.Performance comparison of two filtering approaches for INS rapid transfer alignment[C]//Proc IEEE Conf Mechatronics and Automation.Harbin,China,2007:1956-1961.
[6] Noureldin A,Tabler H,Irvine-Halliday D,et al.A new technique for reducing the angle random walk at the output of fiber optic gyroscopes during alignment processes of inertial navigation systems[J].Journal of Optical Engineering,2001,40(10):2097-2106.
[7]刘建业,曾庆化,赵伟,等.导航系统理论与应用[M].西安:西北工业大学出版社,2010:89-91.
[8] Paul D G.Optimising the transfer alignment of weapon INS[J].Journal of Navigation,2003,56(2):323-325.

