一类MIMO非线性不确定系统的自适应无源控制

朱永红 费树岷

(1景德镇陶瓷学院机械电子工程学院，景德镇 333001)

(2东南大学自动化学院，南京 210096)

无源性概念广泛存在于物理学、应用数学以及力学等领域.它在控制领域里的应用起源于超稳定性、正实性等方面，后经控制工作者的努力形成了系统无源性理论［1］.无源性理论的主要思想是系统的无源性可使系统内部保持稳定.因此，为了使系统稳定，可以利用无源性理论使得闭环系统无源，从而进行控制器的设计.近十几年来，无源性理论在非线性系统的镇定控制器设计中发挥了重要的作用［2-5］.研究表明，无源控制方法的主要特征就在于控制器设计能够很好地利用系统结构特点，无源控制有着清晰的物理意义，具有便于控制的优势以及良好的鲁棒性，因此受到研究人员的广泛关注［1-9］.

近年来，在非线性不确定系统自适应无源化研究方面，取得了一些研究成果［6-9］.文献［6］应用速度-梯度方法，结合反馈无源化理论，研究了一类含凸性未知参数且相对度为1的弱最小相位非线性系统的自适应反馈无源化问题.文献［7］针对一类由可反馈严格无源化的子系统内联的多输入非线性系统，运用反演法逐步实现系统的反馈无源化.文献［8］解决了一类相对度大于1且不稳定的非线性系统的自适应反馈无源化问题.文献［9］基于神经网络用无源方法，研究了一类MIMO非线性不确定系统的自适应输出反馈镇定问题.含有未知参数不确定MIMO非线性系统的自适应无源控制方法目前尚未见有报道.因此，本文在以上研究的基础上，针对一类MIMO非线性系统提出了反馈控制律和参数适应律，实现了这类系统的自适应无源控制.对算例的仿真结果表明，所设计的控制器是有效可行的.

1 问题描述

考虑如下的MIMO非线性系统:

式中，x∈Rn为状态;u∈Rm为控制输入;y∈Rm为输出信号;f和g为C∞向量场;h为光滑映射.假设向量场f至少有一个平衡点，不失一般性，可以假定f(0)=0，h(0)=0.令U为允许的输入集，并假设∀u∈U 以及∀x0=x(0)∈Rn，系统(1)输出y(t)=h(φ)(其中，φ =φ(t，x0，u)表示 f(x)+g(x)u 的流，∀x0∈Rn和∀u∈U)使得，即系统(1)储存的能量是有界的.许多机械和电子机械系统等都有这种特性，并且这种特性广泛地应用于控制目的.

如果假设x=0的邻域Lgh(x)≠0，那么系统(1)在x=0的邻域相对阶［6］为1.存在坐标变换z(x)，使系统能够变换成如下形式［1］:

因此，系统(2)可以写成［1］

现考虑如下含有未知常参数矩阵的不确定MIMO非线性系统:

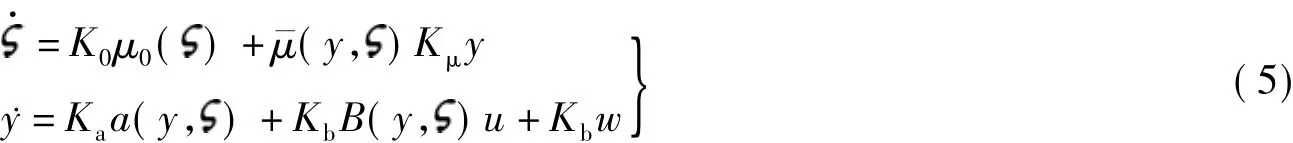
定义1［1］对于系统(1)，若存在Cr非负定存储函数V(x)(V(0)=0)使得不等式

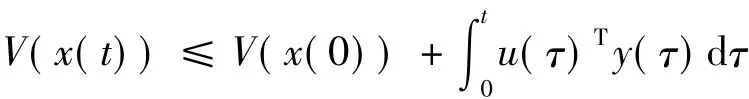
对于任意输入函数u(τ)以及x(0)∈Rn，t≥0成立，则称系统(1)是Cr无源的，该不等式称为无源不等式.本节中只考虑V为连续可微的情况.

本文研究的目的是:设计控制器u，使得参数能够自适应调节，并且使得系统(5)无源.

为了讨论问题方便，先作如下假设:

假设2［1］存在正定可微函数的邻域内满足如下不等式:

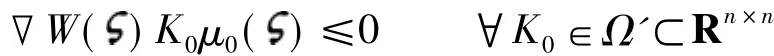
2 自适应反馈无源控制器的设计

2.1 Kb＞0(正定)时控制器的设计

假设3 矩阵Kb∈Rm×m是对称并且正定的矩阵.

定理1 考虑具有未知参数矩阵非线性系统(5)，并假定其满足假设1～假设3，则存在如下控制器:

使得系统(5)为从输入 w 到输出 y的无源系统.式中，矩阵为可调整的参数矩阵;参数误差定义为，其中理想值 θ1，θ2，θ3分别定义为

证明 由式(5)和(6)组成的闭环系统的存储函数为

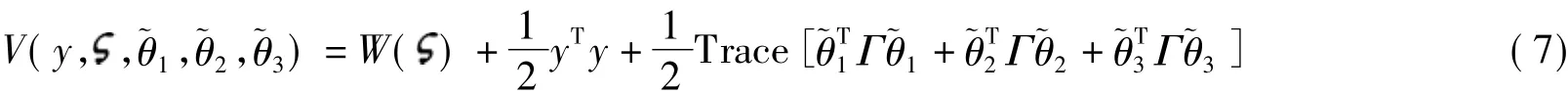
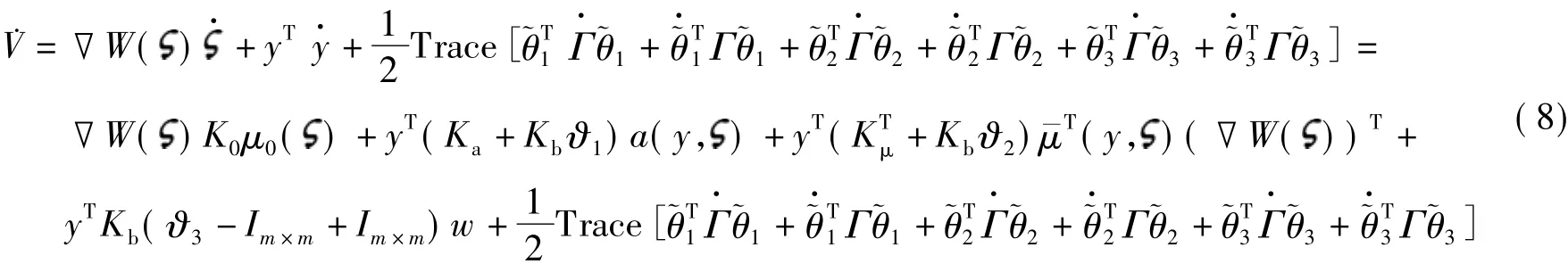
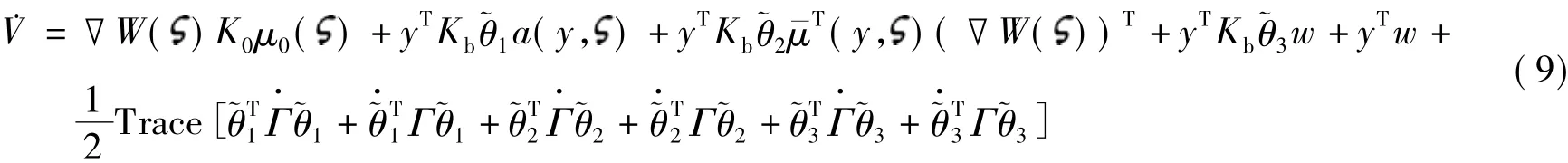
利用2个向量的特性aTb=bTa=Trace(abT)=Trace(baT)，于是有

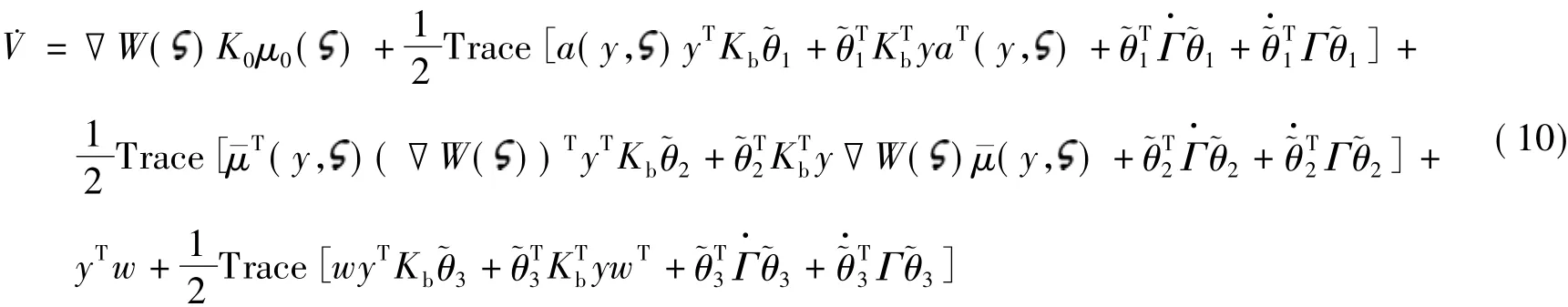
将式(6)中自适应律代入式(10)，并选取正定对称阵Γ=Kb＞0，根据假设2，有

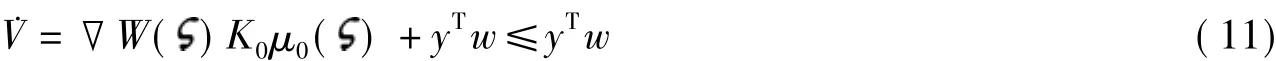
因此，闭环系统由输入w到输出y是无源的.证毕.值得注意的是，当w=0时，由式(11)可知，由式(5)和(6)组成的闭环系统V˙≤0，由式(7)可知，正定.因此，当输入为0时闭环系统为Lyapunov意义上局部稳定.如果假设1和假设2全局满足，那么当输入为0时，闭环系统为Lyapunov意义上全局稳定.如果系统(5)中Kb已知，那么由定理1的证明可以直接得出以下推论.

推论1 考虑如下非线性系统:

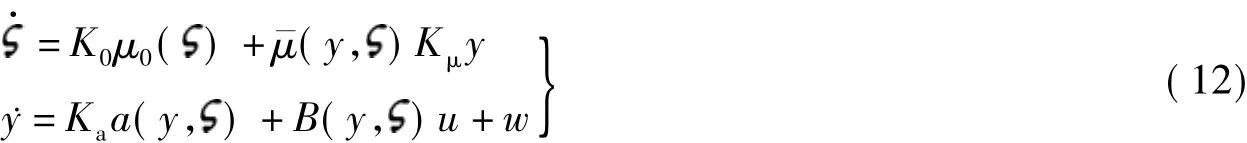
式中，K0，Kμ，Ka为未知参数.假定系统满足假设1和假设2，那么控制器

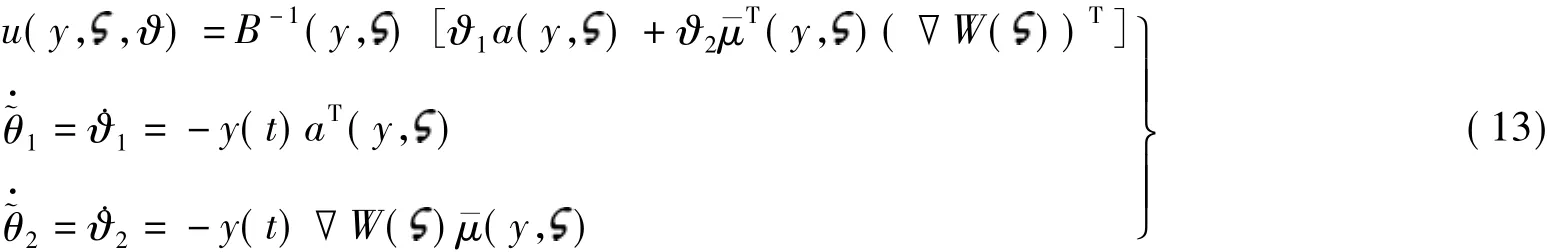
使得系统为输入w到输出y的无源系统.证明方法同前(略).值得注意的是，如果由式(5)和(6)组成的闭环系统状态(y)局部零状态可检测，那么可以通过输出反馈，如w=－Ky(K＞0)，使得闭环系统在平衡点局部渐近稳定，控制器参数ϑi(i=1，2，3)收敛到有界常值.

2.2 Kb为一般常数阵时控制器的设计

在给出Kb为一般常数阵时，反馈无源问题解之前，先引入如下假设

假设4 矩阵Kb∈Rm×m可逆.

定理2 考虑具有未知参数矩阵的非线性系统(5)，并且满足假设1，假设2和假设4，那么控制器

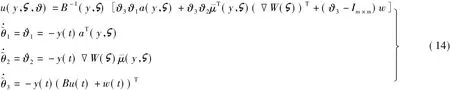
使得由式(5)和(14)组成的闭环系统从输入w到输出y是无源的.式中，Im×m为Rm×m单位阵;ϑ1(t)，ϑ2(t)，ϑ3(t)为可调参数矩阵;参数误差定义为，其中理想值 θ1，θ2，θ3分别定义为

证明 由式(5)和(14)组成的闭环系统的存储函数为

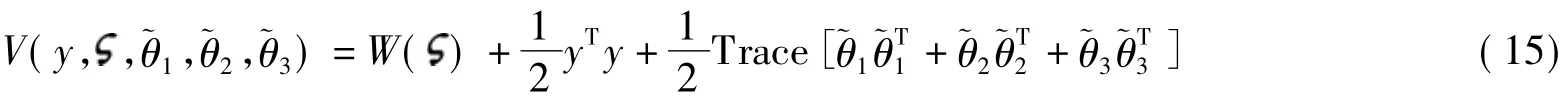
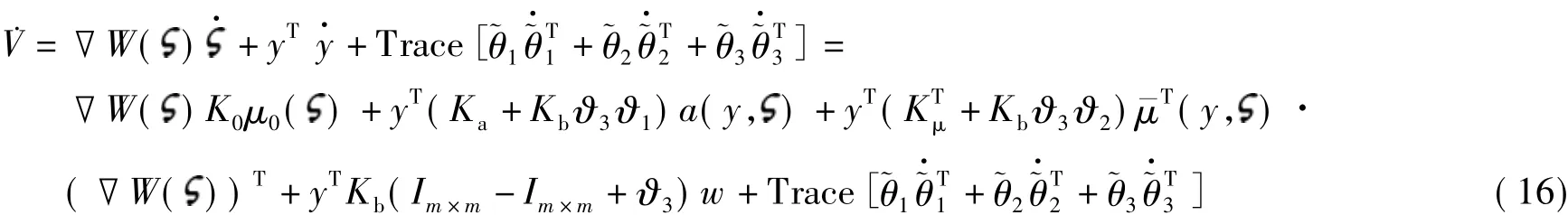
定义理想值 Ka+Kbθ3θ1=0，即.同时定义偏差变量(即参数误差).将这些定义代入式(16)可得

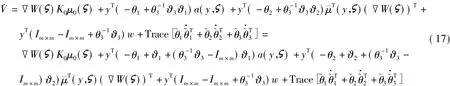
使用参数误差定义，可将式(17)变换为

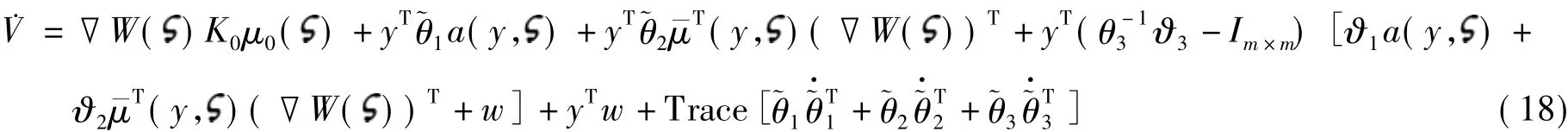
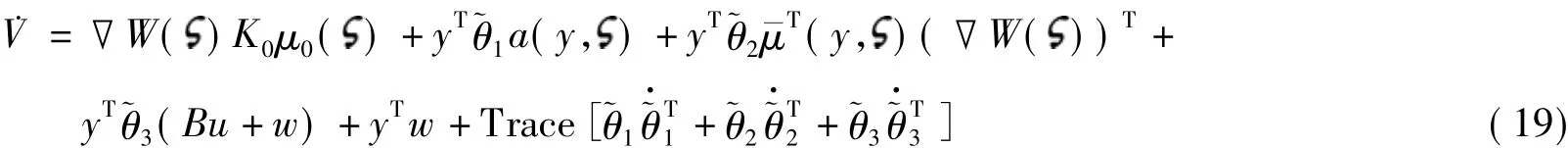
利用2个向量的特性aTb=bTa=Trace(abT)=Trace(baT)，可将式(19)变换为

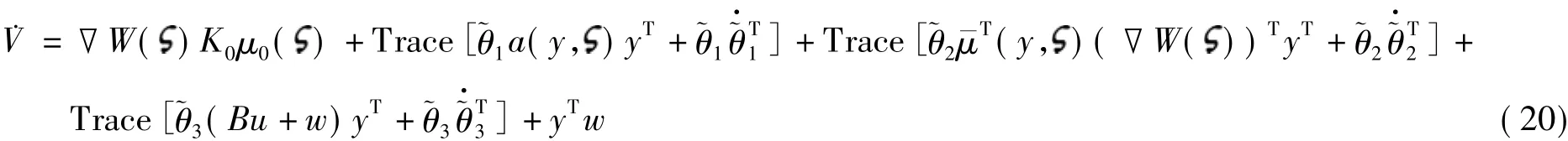
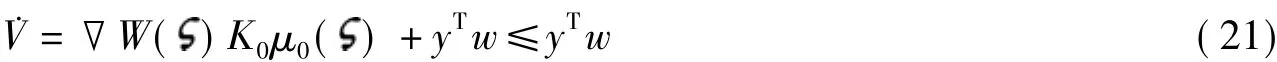
由此可知，闭环系统由输入w到输出y是无源的.证毕.

值得注意的是，当w=0时，由式(21)可知式(5)和(14)组成的闭环系统V˙≤0，并且由式(15)可知正定，因此当输入为0时闭环系统为Lyapunov意义上局部稳定.如果假设1和假设2全局满足，那么当输入为0时，闭环系统为Lyapunov意义上全局稳定.

如果系统(5)中Kb已知，那么由定理2的证明可以直接得出推论1.

3 仿真计算

考虑如下的MIMO非线性系统:

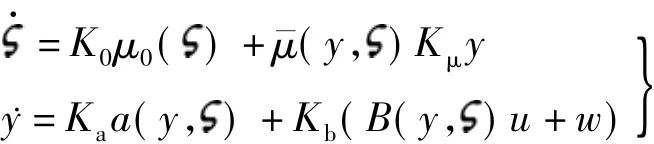
式中，

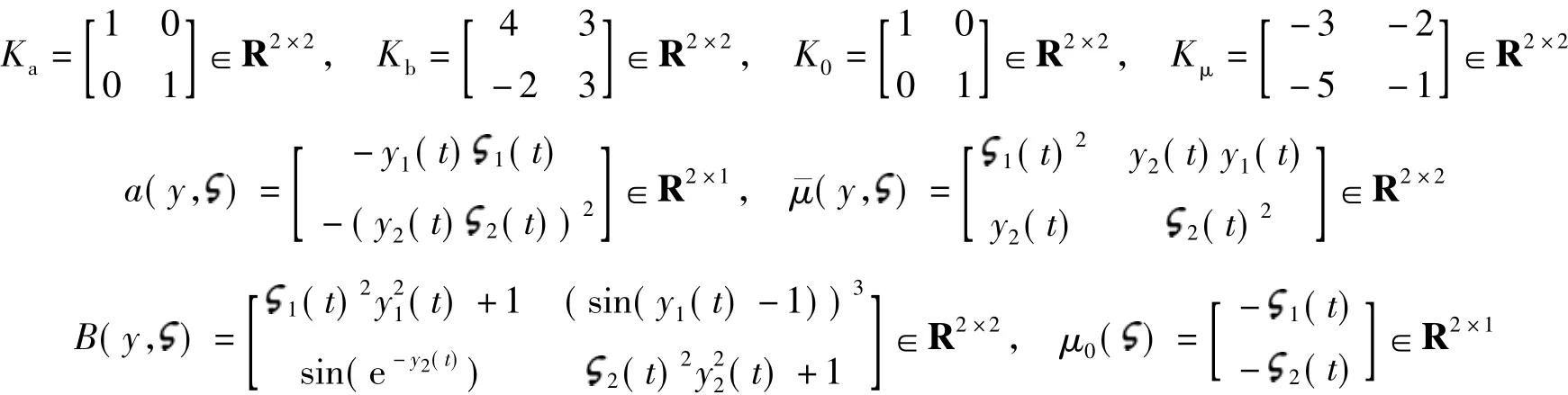
图1 状态1，2的响应曲线

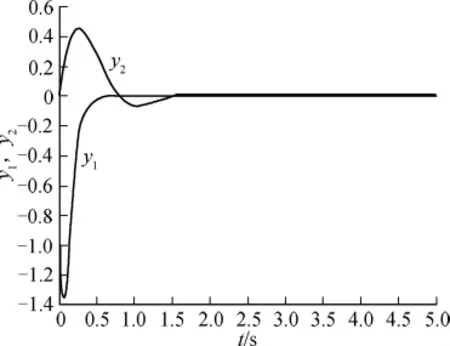
图2 输出y1，y2的响应曲线

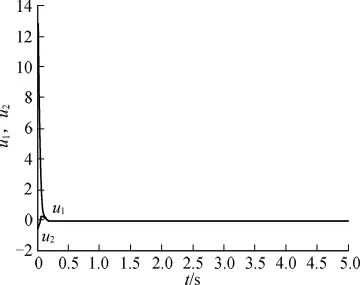
图3 控制输入u1，u2

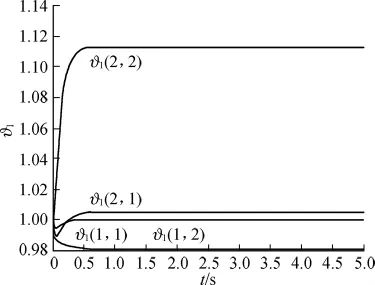
图4 参数ϑ1的响应曲线

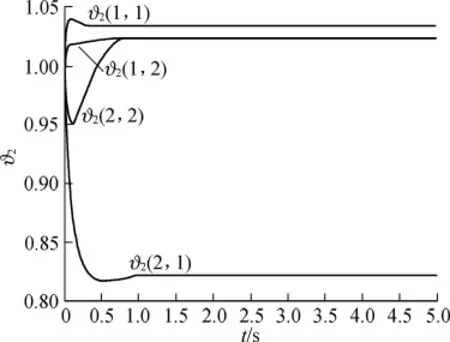
图5 参数ϑ2的响应曲线

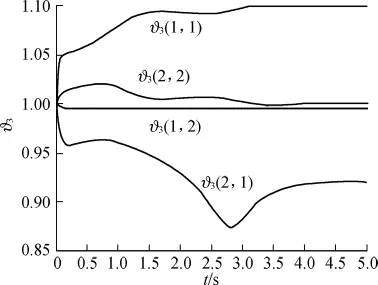
图6 参数ϑ3的响应曲线

4 结语

本文针对一类含有参数不确定多输入多输出非线性系统，讨论了其自适应无源控制问题，提出了其自适应无源控制方案和参数自适应律.在一定的假设情况下，基于Lyapunov方法，证明了所设计的自适应控制器能够保证系统稳定.仿真结果表明，所设计的控制器和参数自适应律能够使得参数自适应调节，并使得系统稳定.因此，本文方法是有效可行的.

References)

［1］ Byrnesc I，Isdori A，Willems J C.Passivity，feedback equivalence and the global stabili-zation of minimum phase nonlinear systems［J］.IEEE Trans Automatic Control，1991，36(11):1228-1240.

［2］ Wu L.Global robust stabilization of minimum-phase nonlinear systems with uncertainty［C］//Proceedings of the 34th IEEE Confonerence on Decision and Control.New Orleans，LA，USA，1997，33:453-462.

［3］ Espinosa-Pérez G，Maya-Ortiz P，Velasco-Villa M，et al.Passivity-based control of switched reluctance motors with nonlinear magnetic circuits［J］.IEEE Trans Control System Technol，2004，12(3):439-448.

［4］ Leyva R，Cid-Pastor A，Alonso C，et al.Passivity-based integral control of a boost converter for large-signal stability［J］.IEE Proc Control Theory Appl，2006，153(2):139-146.

［5］ Wei D Q，Luo X S.Passive adaptive control of chaos in synchronous reluctance motor［J］.Chinese Phys B，2008，17(1):92-97.

［6］ Seorn M M，Hill D J，Fdarkov A L.Nonlinear adaptive control of feedback passive systems［J］.Automatica，1995，31(7):1053-1060.

［7］ Jiang Z P，Hill D J，Fardkov A L.A passification approach to adaptive nonlinear stabilization［J］.Systems and Control Letters，1996，28(2):73-84.

［8］ Kokotovic P V，Krstic M，Kanellakopoulos I.Backstepping to passivity:recursive design of adaptive systems［C］//Proceedings of the 31st IEEE American Control Conference.Chicago，IL，USA，1992:3276-3280.

［9］Kostarigka A K，Rovithakis G A.Approximate adaptive output feedback stabilization via passivation of MIMO uncertain systems using neural networks［J］.IEEE Trans System，Man，and Cybernetics Part B:Cybernetics，2009，39(5):1180-1191.