一类非线性非最小相位系统的指数镇定
张绍杰 胡寿松
(南京航空航天大学自动化学院,南京 210016)
非线性非最小相位系统因其零动态不稳定,成为控制理论和应用研究领域中具有挑战性的问题.反馈线性化是研究非线性控制系统最常用和最有效的方法之一,在非最小相位系统的研究中得到了广泛的应用[1-2].一般的反馈线性化方法是通过对输出求导直到导数中含有输入项,得到系统的相对阶,在此基础上通过微分同胚变换,设计控制律使系统稳定.Soroush等在文献[3-5]中通过对输出求与状态维数相同阶导数,然后在利用小增益理论设计控制律时令输入的导数为零,实现了非最小相位系统的渐近镇定,但由于小增益理论的限制,该方法要求开环系统稳定.在文献[6]中,作者将该方法扩展到了开环不稳定的系统,实现了系统的渐近镇定.在文献[3]的基础上,文献[7]针对单输入单输出(SISO)非最小相位系统,通过近似反馈线性化实现了系统的指数镇定,但由于非线性系统的输入输出耦合,其结论只适用于SISO系统.
本文考虑针对一类多输入单输出(MISO)非最小相位系统,利用近似反馈线性化和零扰动理论,设计系统的指数镇定控制律,仿真算例表明了本文方法的有效性.
1 一类MISO非最小相位系统的指数镇定
1.1 零扰动
考虑系统

式中,φ(x)为标称系统动态,Δ(x)为系统扰动,φ(x),Δ(x)对系统状态x均为Lipschitz的,并记Δ(x)的Lipschitz常数为δ,即‖Δ(x)‖≤δ‖x‖.若Δ(0)=0,即扰动在零时刻的值为零,称为零扰动.对于零扰动系统(1)有如下引理:
引理1[8]若x=0为系统x˙=φ(x)的指数稳定平衡点,系统的Lyapunov函数V(x)满足,,其中c1,c2为正实数.若 Δ(x)的Lipschitz常数 δ满足,则扰动系统(1)的原点指数稳定.
引理1说明原点的指数稳定性对于一定范围内、具有Lipschitz性的零扰动具有鲁棒性.
1.2 一类MISO非最小相位系统的镇定
考虑一类如下描述的MISO仿射非线性系统
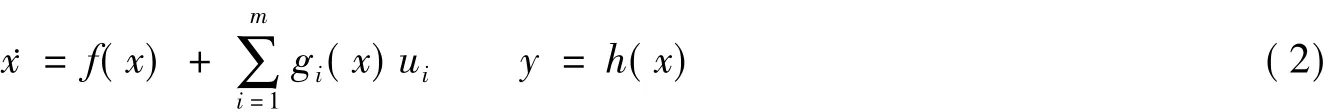
式中,x∈Rn为系统状态向量,u=[u1,…,um]T为系统输入,且 m≥2,y∈R 为系统输出;f(x)∈Rn,h(x)∈R,gi(x)∈Rn,i=1,2,…,m 为关于系统状态 x的充分光滑的非线性函数,并记 g=[g1,…,gm].设 x=0,u=0是系统(2)的平衡点,且 h(0)=0.
假设1 系统(2)满足
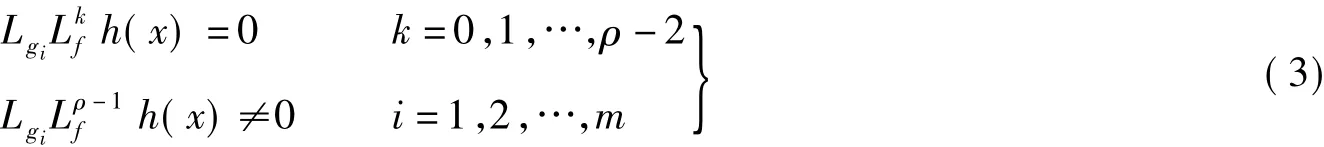
假设1表明对于i=1,2,…,m,˙x=f(x)+gi(x)ui,y=h(x)具有相同的相对阶ρ.对于MISO系统,多个输入一般用来保证控制系统具有一定的余度,以确保系统的安全运行.如飞机上的液压系统,采用3余度设计,多余度采用类似的控制结构.故一般来说MISO系统是满足该假设条件的.

式中,bi(x)为系统状态x的非线性函数,表示第i个执行器对系统控制输入的影响,v0为待设计的控制信号.对系统(2)选取变换
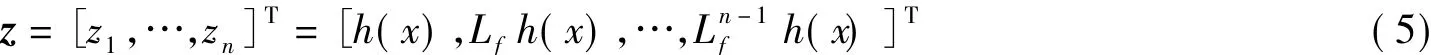
并将式(4)带入系统,则系统(2)可表示为
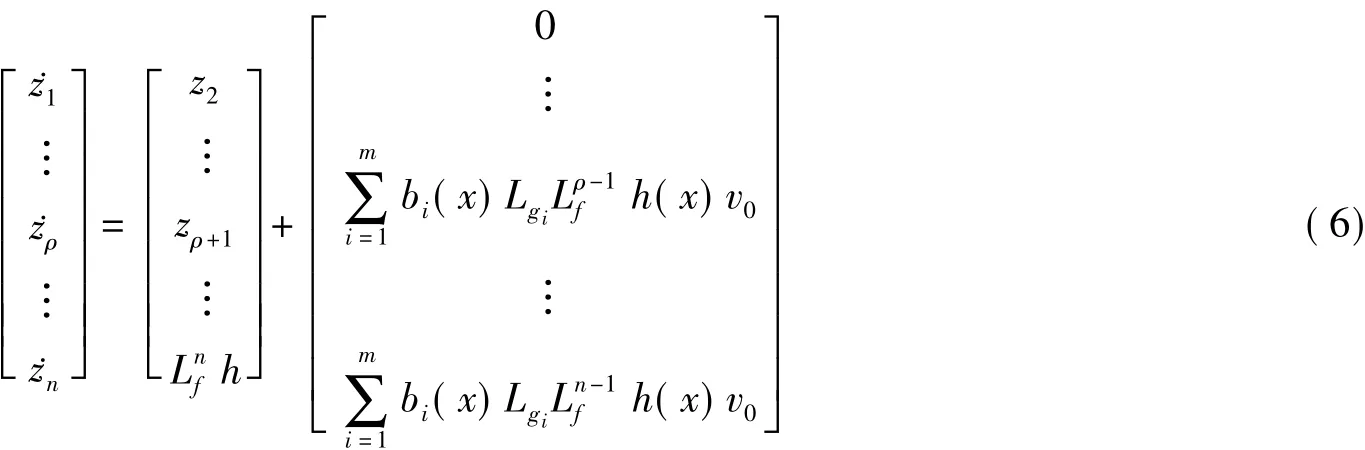
设计控制律


本文采用的变换(5)与常规的将仿射非线性系统变为标准形的变换不一样,在对输出逐次求导过程中,即使出现了输入信号,我们仍继续求导,以实现系统的近似输入输出线性化,对于忽略的部分,我们采用零扰动理论进行处理.于是,对由变换(5),控制律(4)和(7)确定的闭环系统(8)有如下定理:
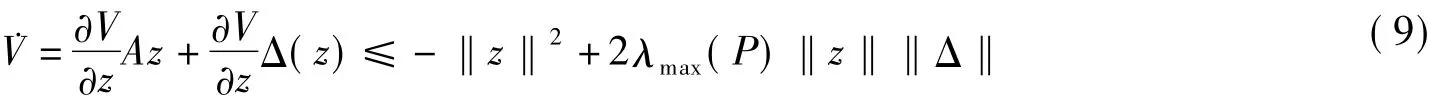

将式(10)代入式(9)得
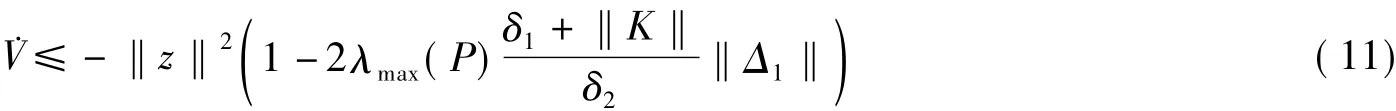
定理1说明对于系统(2),不管其零动态是否稳定,即系统(2)是否为最小相位系统,只要满足定理的条件,则闭环系统(8)指数稳定.
定理1的证明过程表明,对于给定的δ1,δ2和设计的反馈阵K,存在扰动的一个范围使系统(8)指数稳定,但相反地,给定一个扰动,不一定存在相应的反馈阵K能指数镇定该系统.推论1给出了能够使系统指数稳定的扰动范围:
推论1 对于给定的δ1,δ2,在A为Hurwitz矩阵的前提下,记,则当‖Δ1(z)‖<δ*时,存在反馈阵K能够指数镇定系统(8).
证明 略.
2 仿真算例
为验证上文理论的正确性,考虑如下非线性系统
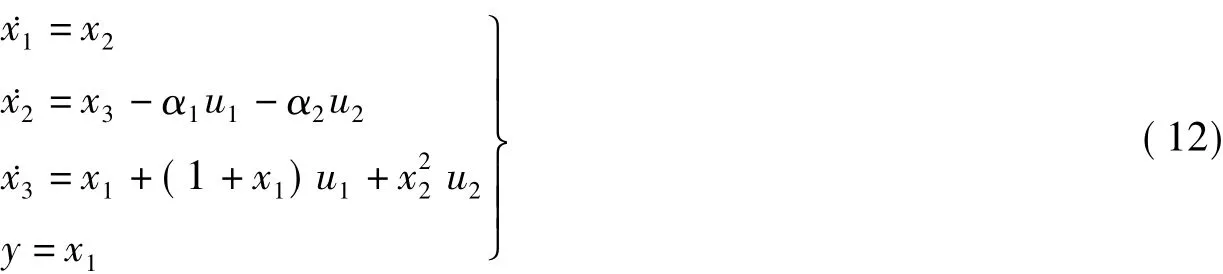
式中,α1,α2>0.系统相对阶为2,采用常规的反馈线性化方法,取

并设计反馈矩阵 K=[32,8],则

系统零动态为˙x3=x3/α1,不稳定,系统为非最小相位系统.设系统初始状态为x(0)=[1,1.5,1.2]T,α1=0.2,α2=0.3,则在控制律(13)和(14)作用下,系统内部状态x3响应曲线如图1所示.
根据式(4)和(7)重新设计控制律,设计反馈矩阵 K=[256,96,16],取

在式(15)和(16)作用下,系统状态响应如图2和图3所示.图2表明采用本文方法设计的控制律可以使系统内部动态稳定,图3表明了外部系统的指数稳定性.改变K,则可以求出系统稳定的初始值范围,从而给出系统的吸引区.
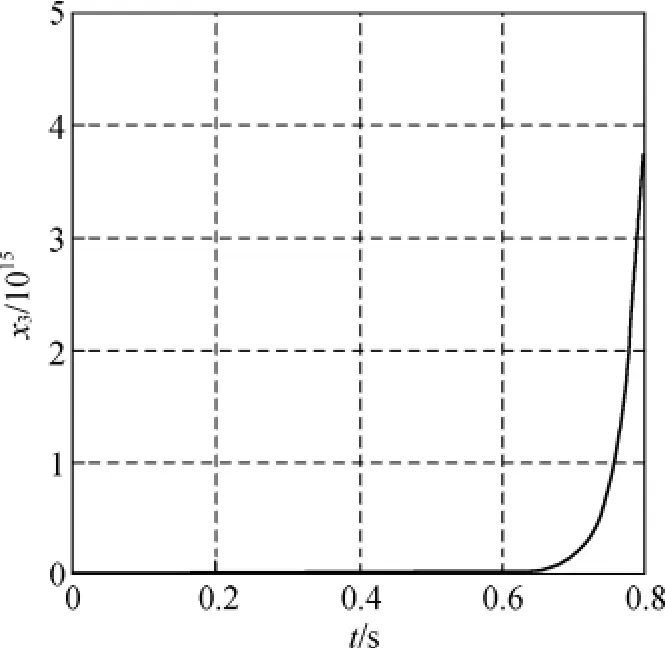
图1 输出反馈线性化x3的响应曲线
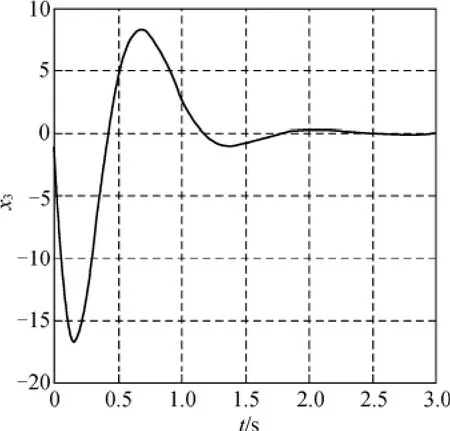
图2 近似反馈线性化x3的响应曲线
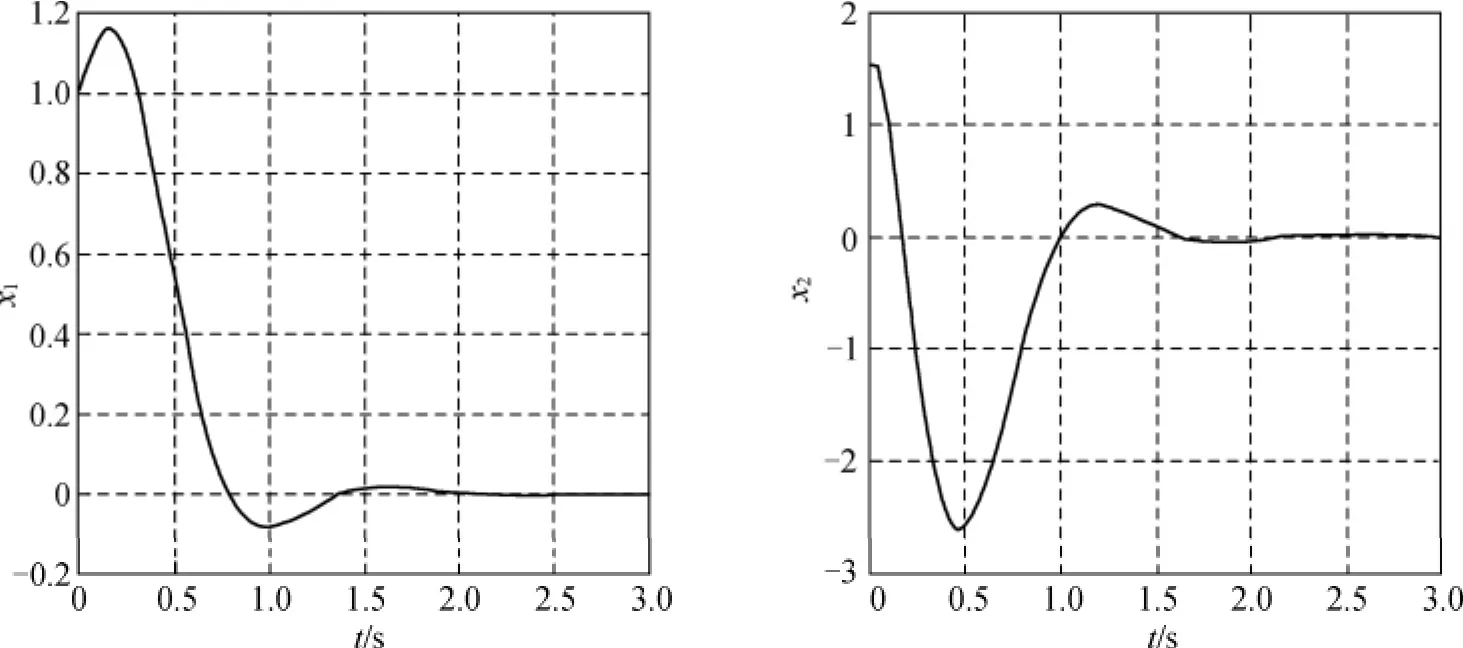
图3 近似反馈线性化状态x1和x2的响应曲线
3 结语
本文针对一类MISO仿射非线性系统,利用近似反馈线性化结合零扰动理论讨论了系统的指数镇定条件,最后结合数学实例进行仿真,说明了控制器的设计过程,进一步证明了本文方法的正确性和有效性.
References)
[1] Guardabassi G O,Savaresi S M.Approximate linearization via feedback—an overview[J].Automatica,2001,31(1):1-15.
[2] Marino R,Tomei P.A class of globally output feedback stabilizable nonlinear nonminimum phase systems[J].IEEE Transactions on Automatic Control,2005,50(12):2097-2101
[3] Soroush M,Kravaris C.A continuous-time formulation of nonlinear model predictive control[J].International Journal of Control,1996,63(1):121-146.
[4] Kanter J M,Soroush M,Seider W D.Continuous-time,nonlinear feedback control of stable processes[J].Ind Eng Chem Res,2001,40(9):2069-2078.
[5]Kanter J M,Soroush M,Seider W D.Nonlinear feedback control of multivariable non-minimum-phase processes[J].Journal of Process Control,2002,12(6):667-686.
[6]Panjapornpon C,Soroush M,Seider W D.Model-based control of unstable non-minimum-phase nonlinear processes[C]//Proceedings of the 42nd IEEE Conference on Decision and Control.Hawaii,2003:6151-6156.
[7]Guemghar K,Srinivasan B,Bonvin D.Approximate input-output linearization of nonlinear systems using the observability normal form [C]//Proceedings of the 7th European Control Conference.Cambridge,2003:1-6.
[8] Khalil H K.Nonlinear System [M].New York:Prentice Hall,2002.

