基于非下采样Contourlet扩散滤波的红外图像降噪
倪 超 李 奇 夏良正
(1南京林业大学机械电子工程学院,南京 210037)
(2东南大学自动化学院,南京 210096)
与可见光图像相比,红外图像具有对比度低、噪声大、边缘模糊等特点,常用的降噪方法在降噪的同时导致边缘更加模糊,不利于后续处理.因此针对红外图像的特点研究一种既能有效去除噪声,又能很好保留边缘等重要信息的处理方法是十分有意义的工作.基于偏微分方程的非线性扩散[1]技术是一种有效的图像降噪技术,通常选用图像梯度作为边缘映射从而区分噪声与信号,保留梯度较高的边缘区域,平滑梯度较低的一致性区域,在降低噪声的同时能有效保留图像细节.为了进一步提高非线性扩散方法的降噪性能,人们尝试将非线性扩散方法与多尺度分析方法结合起来克服相互缺点.Zhong等[2]在小波变换域进行非线性扩散滤波.Lu等[3]基于小波系数的变化作为边缘映射,对子带小波系数利用非线性扩散函数进行迭代收缩降噪.Ni等[4]将非线性扩散过程转换为二进小波收缩过程,实现多尺度扩散降噪.Ma等[5]在curvelet收缩降噪后,通过非线性扩散消除伪吉布斯现象.Zhang等[6]提出了一种金字塔非线性扩散方法(laplacian pyramid nonlinear diffusion,LPND)方法,其对分解后的各尺度金字塔带通图像进行自适应的非线性扩散滤波,在降噪的同时较好地保持了边缘细节与结构,具有良好的视觉效果.然而文献[6]采用的拉普拉斯金字塔分解过程中存在下采样操作,不具有平移不变性,会引起伪吉布斯现象,同时对于那些对比度低、噪声大的红外图像而言,仅仅采用基于图像梯度的非线性扩散方法不能有效地消除噪声.
本文将非下采样Contourlet变换与非线性扩散技术结合起来,提出了一种基于非下采样Contourlet扩散滤波的红外图像降噪算法.首先,对红外图像采用具有平移不变性的多尺度非下采样金字塔进行分解,在带通图像各非下采样金字塔层采用进行基于联合映射的多尺度非线性扩散滤波,从而在降噪的同时保留图像的边缘细节信息.在此基础上采用具有平移不变性的非下采样方向滤波器组对扩散滤波后的非下采样金字塔层带通图像进行多方向性分解,然后基于尺度相关性的阈值化处理非下采样Contourlet系数.实验证明算法能有效实现红外图像降噪的同时保留边缘细节信息,获得更好的视觉效果.
1 非下采样Contourlet变换
Contourlet[7]变换是由拉普拉斯金字塔(laplacian pyramid,LP)和多方向滤波器组 (directional filter bank,DFB)两部分叠加而成的一种多方向多尺度变换.由于在变换过程中存在下采样操作,Contourlet变换并不具有平移不变性,不可避免地会引起伪吉布斯现象.Arthur等[8]通过构造非下采样金字塔(nonsubsampled pyramid,NSP)与非下采样方向滤波器组(nonsubsampled directional filter bank,NSDFB),提出了一种具有平移不变性的非下采样Contourlet变换(nonsubsampled contourlet transform,NSCT),并被成功用于图像降噪[8-10],为图像降噪领域提供了一种崭新的分析处理工具,如图1所示.
2 非下采样Contourlet扩散滤波
非下采样Contourlet扩散滤波包含5个步骤,如图2所示.①对噪声图像进行NSP分解;②非线性扩散NSP带通图像,调整NSP系数;③对扩散滤波后的带通NSP层利用NSDFB进行多方向性分解;④对各多方向子带系数采用基于尺度相关性的阈值化处理;⑤进行NSCT重构,实现图像降噪.一旦图像被分解为频率下降的多层NSP时,由于噪声信号具有高频特性,分解后主要位于NSP的底层,而NSP顶层内噪声基本可以忽略.因此对带通NSP层非线性扩散滤波可以在有效降噪同时保留有用的细节与边缘信息,获得良好平滑的视觉效果.在此基础上对滤波后的NSP进行多方向性分解,结合尺度相关性进一步消除图像噪声,不仅能有效降噪,而且不会产生通常阈值降噪产生的明显振铃、伪吉布斯现象等视觉失真.
2.1 NSP域多尺度非线性扩散滤波
红外图像存在噪声大、对比度低等特点,然而在图像带通NSP层采用梯度作为边缘映射仍旧无法正确区分边缘与噪声.Chen[11]基于尺度相似性理论提出一种非一致性测度.定义像素(x,y)的局部最优尺度:

式中,R和Ts分别是邻域尺寸系数和公差系数;U(x,y)(R)是以像素(x,y)为中心R尺寸邻域内所有像素与像素(x,y)之间的一致性度量.定义基于局部最优尺度Rxy和Rij的空间邻域为
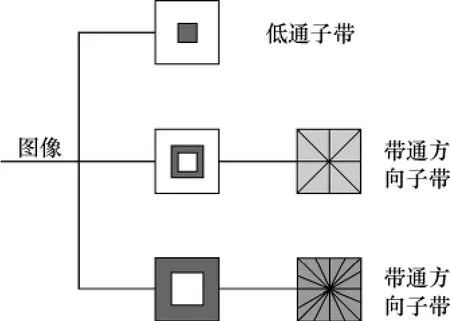
图1 NSCT结构图
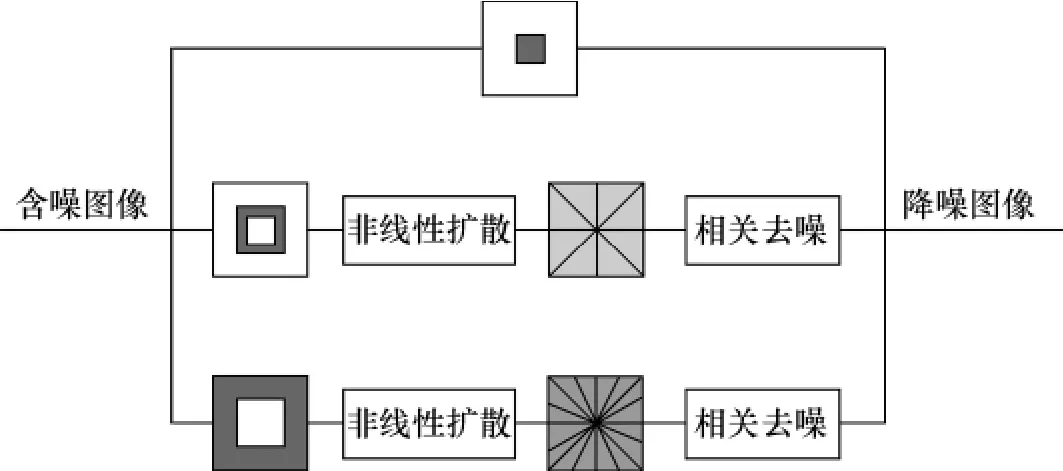
图2 二级NSCT扩散滤波示意图
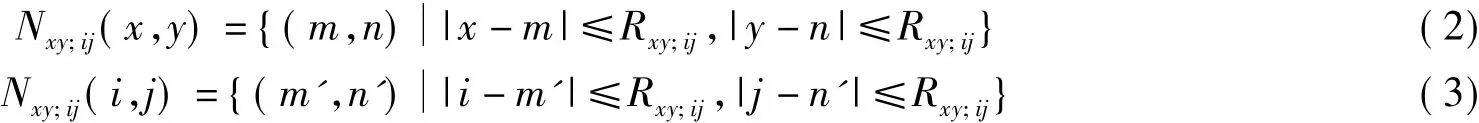
其中,Rxy;ij=min{Rxy,Rij}.以上定义可知,两相邻像素总是具有同样尺寸的邻域,因此可以获得两邻域局部灰度差异.
Chen[11]定义像素(x,y)的非一致性测度为
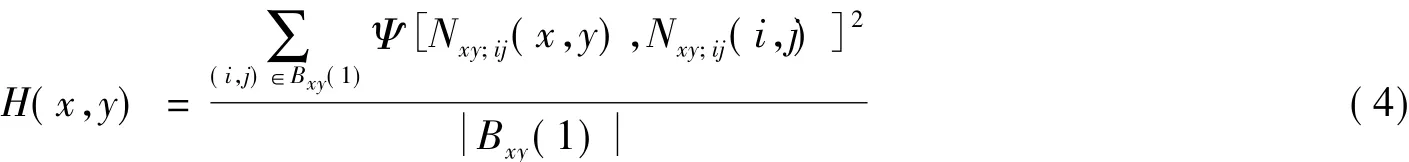
其中,Ψ[Nxy;ij(x,y),Nxy;ij(i,j)]为邻域 Nxy;ij(x,y)和 Nxy;ij(i,j)区域内非一致性测度,当像素(x,y)和(i,j)位于边缘区域或非平凡不连续区域附近时,Ψ[Nxy;ij(x,y),Nxy;ij(i,j)]的数值较大,反之则数值较小.Bxy(1)与|Bxy(1)|分别表示像素(x,y)的最近邻域以及该邻域内像素数目.在此基础上,Chen[11]对归一化的非一致性测度进行非线性变换,从而使得相对于重要图像特征的区域具有更高的非一致性测度.

式中,Hmax和Hmin分别为图像中最大和最小的非一致性测度.非一致性测度 ^H(x,y)能够揭示像素与其周围相邻像素间的内在不一致性,因此其具有更好的抗噪性能.由于非一致性测度能够探测图像场景特征,而图像梯度能够识别图像局部细节,如果将两种不连续性测度有机的结合起来作为扩散过程的边缘映射,从而控制扩散滤波过程,将有在保留边缘细节的同时实现图像降噪,因此设计的NSP域扩散方程如下所示:
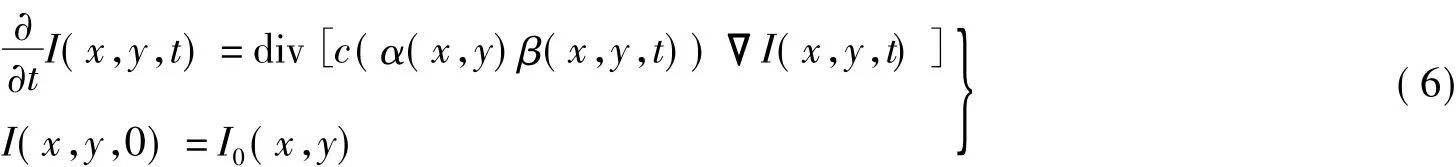
式中,α(x,y)和 β(x,y,t)为
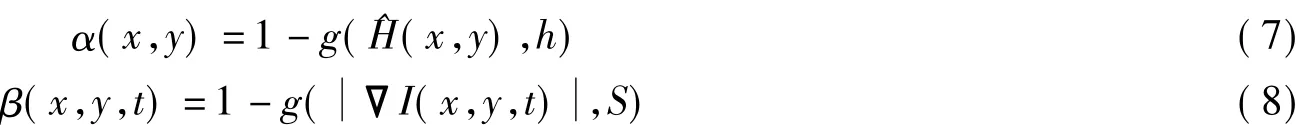
式中,0<g(·,·)<1为单调递减非负函数.参数h(0<h<1)用来根据非一致性测度确定多大程度的潜在重要特征需要保留,同样参数S(S>0)用来确定多大程度的局部图像梯度特征需要保留.本文选取文献[12]提出的扩散系数方程作为本文的扩散方程,则扩散系数方程为
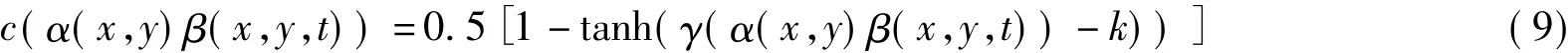
式中,γ控制图像极小极大过渡区域的陡度;k则根据联合边缘映射控制扩散的程度.当像素(x,y)位于一致性相对较好的区域时,α(x,y)和β(x,y,t)取值均较小,多平滑扩散.当像素(x,y)位于边缘区域时,α(x,y)和β(x,y,t)取值均较大,保护边缘细节.当像素(x,y)位于由于噪声产生的虚假边缘区域时,此时虽然基于梯度的β(x,y,t)取值较大,但由于α(x,y)表征了内在场景奇异性其取值较小,因此扩散系数c(α(x,y)·β(x,y,t)) 取值仍较大,平滑扩散消除噪声.
2.2 尺度相关性NSCT降噪
NSP域多尺度非线性扩散滤波可以消除大部分图像噪声,获得良好视觉效果.为了进一步克服噪声的影响,本文对滤波后的带通NSP层进行NSDFB多方向分解,然后对滤波分解后NSCT系数利用尺度相关性实现降噪.基于尺度相关性的小波降噪方法由来已久,最早Xu等[13]利用信号在尺度间相应位置上的小波系数具有很强的相关性,而噪声的小波系数则具有弱相关性或者不相关的特性,将图像经小波变换后相邻尺度同一位置的小波系数的乘积构成相关量,作适当灰度伸缩变后同图像的小波系数进行比较,相关量较大对应的小波系数被划为边缘轮廓等特征,并作为原始信号小波变换的估计,然后经反变换就得到降噪图像.NSCT由于采用类似小波变换的多尺度分解结构,NSCT系数也具有类似小波系数的尺度相关性特征:随着尺度的增加,噪声的NSCT系数将迅速衰减,而边缘轮廓等特征的NSCT系数则相对稳定.因此将文献[13]中的小波降噪算法推广到NSCT域,对NSCT系数采用基于尺度相关性硬阈值降噪.由于NSP域多尺度非线性扩散方法已消除大部分图像噪声,且图像平滑视觉效果良好,因此对NSCT多方向子带进行阈值降噪在图像重构后不会产生明显的振铃、伪吉布斯现象等视觉失真.算法步骤如下:
①计算各方向子带系数的尺度相关量,相关量定义为相邻两尺度同一空间位置上的NSCT系数的乘积,则对于尺度j,l方向子带,位置(x,y)的NSCT系数的相关量:
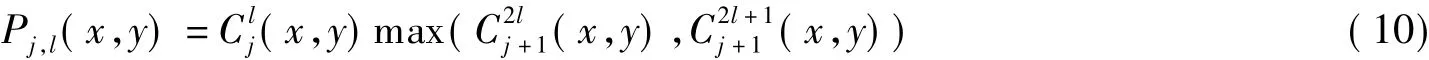
②归一化相关量,使其具有可比性:
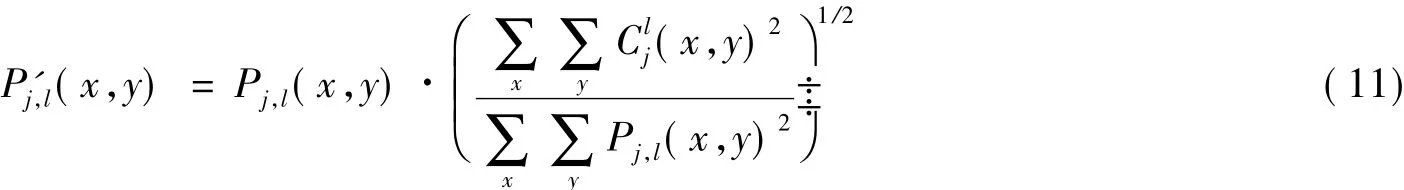
③ 对于尺度j,l方向子带,位置(x,y)的点,采用硬阈值降噪.如果,则置(x,y)=0.其中k为随尺度增加而减小的权值因子.
3 实验结果分析
算法的目的是抑制红外图像噪声的同时保持图像边缘,分别采用加入高斯白噪声的红外吉普车与直升飞机图像进行仿真实验,并与非线性扩散[1]、LPND[6]相比较.本文对所有图像均采用三级NSCT扩散滤波结构,三级分解的方向数分别为8,4和2.表1为吉普车图像各种方法处理的SNR.从表1可以看出当噪声信号较弱时3种方法降噪性能大体相当,但随着噪声信号的增强,非线性扩散方法采用图像梯度作为边缘映射,无法正确区分边缘与噪声,降噪性能明显降低.LPND法由于结合金字塔分解的信噪分离特性,在多尺度带通金字塔层非线性扩散,降噪性能优于非线性扩散,本文算法在带通NSP层采用基于非一致性测度的联合边缘映射,多尺度平滑扩散,同时结合NSCT多方向性特征利用尺度相关性进一步降噪,具有较好的降噪性能.对比实验如图3所示,图3(a)为加入方差σ=0.02高斯白噪声的红外直升飞机图像;图3(b)为非线性扩散法的处理结果;图3(c)LPND法的处理结果;图3(d)为本文算法的处理结果.图3(b)、(c)虽图像有朦胧感,边缘模糊;显然,非线性扩散法与LPND法的结果图像模糊,螺旋桨部分丢失,相比较而言本文算法仍具有较好的降噪与边缘保持性能.从仿真结果可以看出本文算法在不同噪声方差条件下能取得较好SNR,且结果图像平滑、边缘清晰,是一种有效的红外图像降噪算法.然而算法运行时间相对较长,在P4 3.0 G内存512 M机器上运行matlab程序对大小为320×240的红外图像进行处理,每次运行时间大约15 s,时间主要花费在NSCT分解重构过程,相信采用编译型语言进行实现,算法的执行效率会有很大提高.

表1 吉普车图像各种方法处理的SNR dB

图3 对比实验-红外直升飞机图像处理结果
4 结语
针对红外图像的特点,提出了一种基于非下采样Contourlet扩散滤波的红外图像降噪算法.首先,对红外图像进行多尺度非下采样金字塔分解,利用基于联合边缘映射的非线性扩散滤波各非下采样金字塔层带通图像,在降噪的同时保留图像的边缘细节信息.为了进一步消除图像噪声,采用非下采样方向滤波器组对扩散滤波后的各非下采样金字塔层图像进行多方向性分解,对分解后的非下采样Contourlet系数进行基于尺度相关性的阈值处理.实验证明算法能有效实现红外图像降噪的同时保留更多边缘细节信息,获得更好的视觉效果.
References)
[1] Perona P,Malik J.Scale-space and edge detection using anisotropic diffusion[J].IEEE Trans Pattern Anal Mach Intell,1990,12(7):629-639.
[2] Zhong J M,Dardzinski B,Holland S,et al.Wavelet-based multiscale anisotropic diffusion for MR imaging[C]//Proceedings of SPIE Medical Imaging,San Diego,USA,2005:1046-1053.
[3]Lu P Y,Satou A,Miyamoto M,et al.Novel denoising technique based on filtering the coefficients of a redundant wavelet transform[J].Optical Engineering,2007,46(4):043202.
[4] Ni C,Li Q,Xia L Z.A novel method of infrared image denoising and edge enhancement[J].Signal Processing,2008,88(6):1606-1614.
[5] Ma J W,Plonka G.Combined curvelet shrinkage and nonlinear anisotropic diffusion[J].IEEE Trans Image Processing,2007,16(9):2198-2206.
[6] Zhang F,Yoo Y M,Koh L M,et al.Nonlinear diffusion in laplacian pyramid domain for ultrasonic speckle reduction[J].IEEE Trans Medical Imaging,2007,26(2):200-211.
[7] Do M N,Vetterli M.The contourlet transform:an efficient directional multiresolution image representation[J].IEEE Trans Image Processing,2005,14(12):2091-2106.
[8] Arthur L,Zhou J P,Do M N.The nonsubsampled contourlet transform:theory,design,and applications[J].IEEE Trans Image Processing,2006,15(10):3089-3101.
[9] Qiang Sun,Licheng Jiao,Biao Hou.Synthetic aperture radar image despeckling via spatially adaptive shrinkage in the nonsubsampled contourlet domain[J].J Electron Imaging,2008,17(1):013013.
[10]张林,朱兆达.基于非降采样 Contourlet变换的非线性图像增强新算法[J].电子与信息学报,2009,31(8):1786-1790.Zhang Lin,Zhu Zhaoda.A novel nonlinear method for image enhancement based on nonsubsampled contourlet transform[J].Journal of Electronics&Information Technology,2009,31(8):1786-1790.(in Chinese)
[11] Chen K.Adaptive smoothing via contextual and local discontinuities[J].IEEE Trans Pattern Anal Mach Intell,2005,27(10):1552-1566.
[12] Monteil J,Beghdadi A.A new interpretation of nonlinear anisotropic diffusion for image enhancement[J].IEEE Trans Pattern Anal Mach Intell,1999,21(9):940-946.
[13] Xu Y,Weaver B,Healy D,et al.Wavelet transform domain filters:a spatially selective noise filtration technique[J].IEEE Trans Image Processing,1994,3(5):747-758.

