电离层空时相位特性对天波海态雷达影响研究

李 雪 邓维波 刘 聪 邹积虹

(1.哈尔滨工业大学,黑龙江 哈尔滨150001;2.中国电波传播研究所,电波环境特性及模化技术重点实验室,山东青岛266107)

1.引 言

高频天波海态雷达利用电离层折射实现超远距离、大范围海态监测,获取风向、风速、洋流、浪高等多种海态参数[1-3]。电离层是天波海态雷达的重要传输媒质,其特性对天波海态雷达探测能力产生巨大影响。

天波海态雷达接收系统采用大型天线阵列提高方位分辨率。众所周知,阵元的加工尺寸和间距,接收通道间的差异影响了数字波束形成(DBF)质量。但这些差异可通过天线校准和通道校准事先估计,加以抑制。另外,各阵元接收到的回波信号是由相邻较近的不同电离层反射回来,对每个阵元回波信号附加的相位略有不同,特别是当电离层存在不均匀体时,将严重影响回波信号的空间相干性,导致水平方向图主瓣变宽,副瓣抬高,方位分辨率下降。文献[4]采用空间相关算法(SCA)改善方位分辨能力。

电离层多层结构导致天波海态雷达多模式效应,使得不同地面距离的杂波落入同一雷达射线距离单元,杂波频谱展宽,影响风速、风向、洋流、浪高谱等海杂波参数反演精度。高频天波海态雷达频率管理系统实时选择合适的工作频率,可以最大可能地避免多模式传播效应[5]。

电离层的非平稳性引起高频天波海态雷达回波信号相位路径扰动,使得不同脉冲重复周期内同一距离单元信号时间相关性变差,多普勒分辨率下降,同样影响海杂波参数反演精度。估计和校正电离层非平稳性引起相位污染的有效方法之一是在所需观测区内设置应答器[6]。实际工程中,架设应答机受到环境条件等限制,无法做到全部观测范围内的使用。因此,通常利用先验的雷达地、海杂波信息取代应答器。目前,天波海态雷达解电离层相位污染广泛应用时域估计补偿方法,比较流行的算法有基于最大熵谱估计法[7]、相位梯度自聚焦[8]、时频分析[9]、基于特征分解[10]、分段多项式相位建模[11-12]等解污染方法。

虽然,目前关于电离层空时相位特性对天波海态雷达的影响提出了诸多抑制方法,但均受一定的条件或场合限制[13]。要想彻底解决这一问题,必须深入研究电离层空时相位随机变化特性如何影响天波海态雷达后续信号处理。本文首次引入相延时和群延时,重新推导了天波海态雷达回波信号处理表达式,通过严格的理论推导,深入分析了电离层空时相位变化对天波海态雷达方位波束宽度、杂波频谱影响,并利用仿真方法进行了验证。最后,利用空时信号处理对上述展宽进行了抑制,取得一定成效。

2.群延时与相延时

电离层为色散、各向异性、有耗的复杂介质,对经过它的无线电波产生复杂影响。

电离层中无线电波传播的折射指数由Appleton-Hartree公式[11]给出

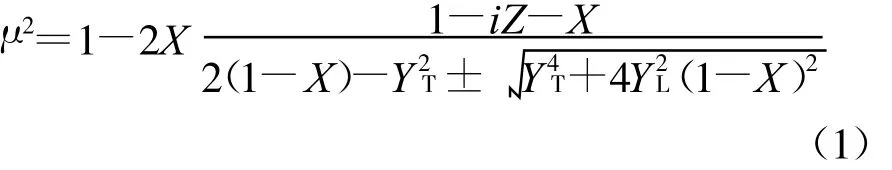
式中:X=f2N/f2,为等离子体频率;Y=/f,为磁旋频率;为Y垂直于波法向的分量,=Y sinθ;YL为Y平行于波法向的分量,YL=Y cosθ;θ是电波法向与地磁场夹角;Z=ν/2πf,ν为电子碰撞频率。

由Appleton-Hartree公式可以看出:由于存在地磁场,电离层等离子体是各向异性的,折射指数μ依赖于波法线方向,因此,射线方向和波传播方向常常是不同的,在各向异性媒质中射线传播如图1所示。

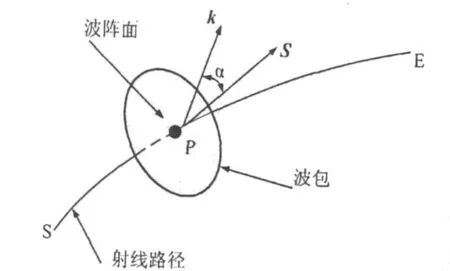
图1 各向异性媒质中电波传播示意图

射线路径上S、E之间的相位差为

式中:k为波矢量;α为波法向与射线方向的夹角。产生Δφ相位差所需要的时间,即波阵面从S到E的时间称为相延时τp

等相位面所传播的距离,称为相路径P

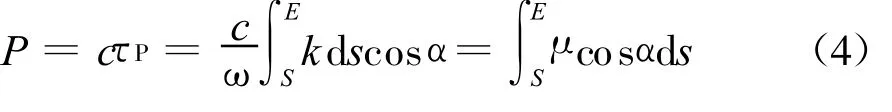
式中,μ为相折射指数。信号包络从S传播到E的时间称为群延时τg

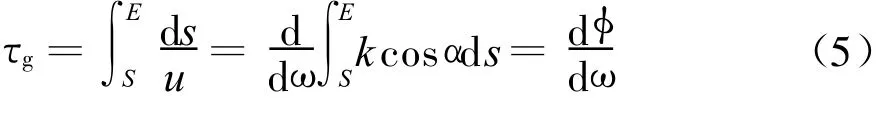
式中,u为群速度。该传输时间乘以光速便等效为在自由空间传播τg后波包所传播的距离,称为群路径 P′,μ′为群折射指数 ,则

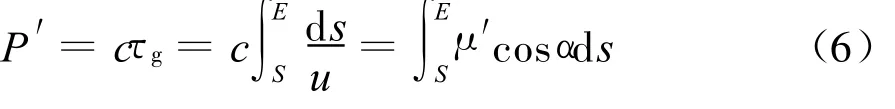
从上面可以看出:相路径和群路径只是一个时间的度量,并不代表真正的传播路径,唯一存在的路径是能量传输的路径

3.天波海态雷达信号处理表达式推导

对天波海态雷达系统而言,由于干扰和电离层色散带宽的限制,发射信号通常为窄带的线性调频连续波,其表达式如下[14]

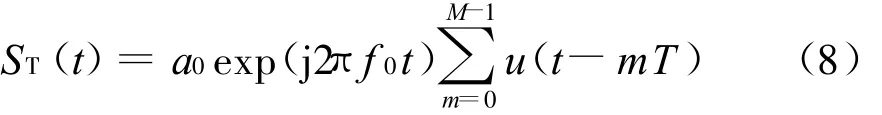
式中:

式中,m表示脉冲数目。正如前面分析,发射信号经过电离层后,幅度、相位均受到调制,且信号包络按群路径传播,等相位面按相路径传播,接收信号可表示为

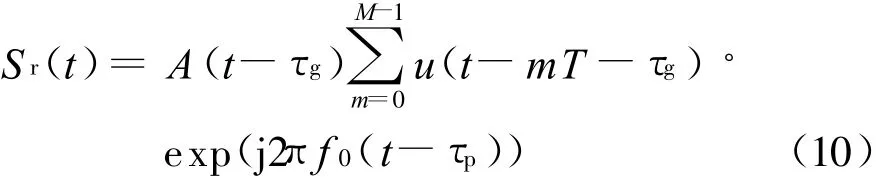
为了简化问题,仅考虑电离层相位特性对回波信号影响,设 A(t-τg)=a0为常数。

设t时刻相路径为R p(t),初始相路径为R p(0),接收信号的相延时由t-τp/2时刻的电离层状态和目标位置确定。

同理,对于群延时

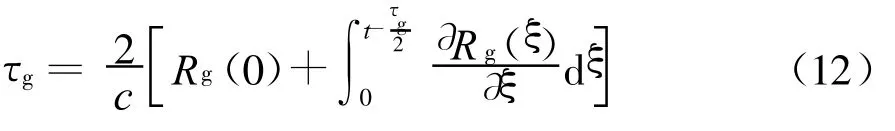
天波海态雷达采用脉冲压缩、阵列数字波束形成和相干积累技术提升探测能力,对应于距离、方位、多普勒三维信号处理。海杂波散射具有面目标特性,目前的天波海态雷达大多采用较大的天线阵列,回波距离-方位分辨单元内海杂波特性可近似相同,即对于某一距离-方位分辨单元杂波回波信号可按照点目标进行处理。同时考虑本文推导结果,可应用于其它天波目标检测雷达,不失一般性,针对点目标进行三维信号处理表达式推导。

3.1 距离维回波信号处理表达式推导

天波海态雷达回波信号的距离维处理通常有两种方法:一种是匹配滤波,另一种是去斜。两种方法没有本质区别,处理结果基本相同。本文仅给出采用去斜方法进行距离维处理的公式推导。

设某个目标的方位角为α、径向速度为νr,相干积累脉冲数目为M,接收阵元数目为N,则第m个脉冲周期第n个接收阵元接收信号回波形式为

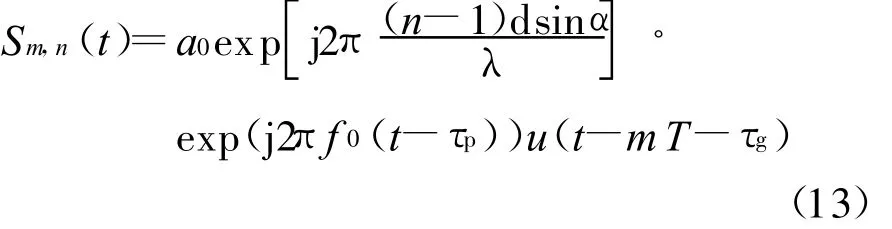
考虑接收参考距离为0 km,接收参考信号为

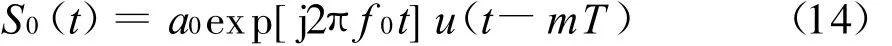
回波信号与参考信号混频、经过低通后表示为

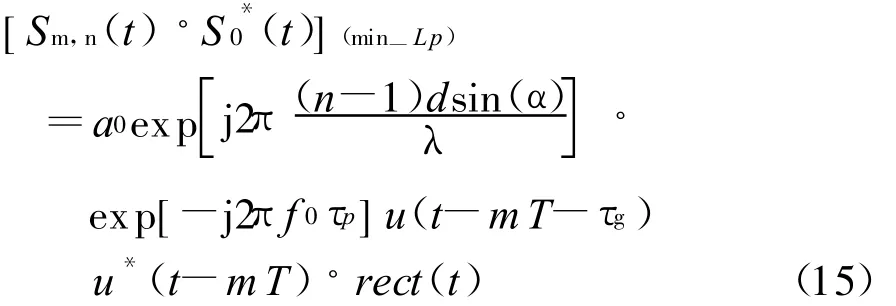
式中:

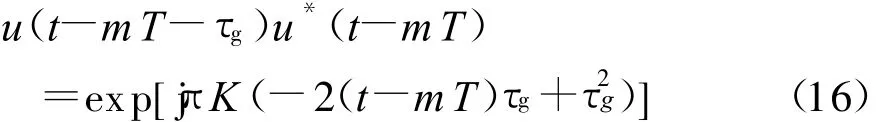
式中:

对天波海态雷达,目标回波距离及距离分辨单元都远大于群路径的某个扫频脉冲时间内的变化量,可认为群路径仅随时间变量mT变化。即式(12)可简化为

其中,R gm(0)=R g(0)+ΔR g(mT),ΔR g(mT)表明了由于电离层时变特性,不同扫频周期段上群路径略有差别,但远小于距离分辨单元。

将式(11)、(16)、(17)代入式(15)得

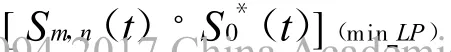
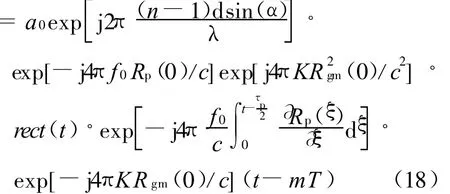
对式(18)中第四行做如下处理:

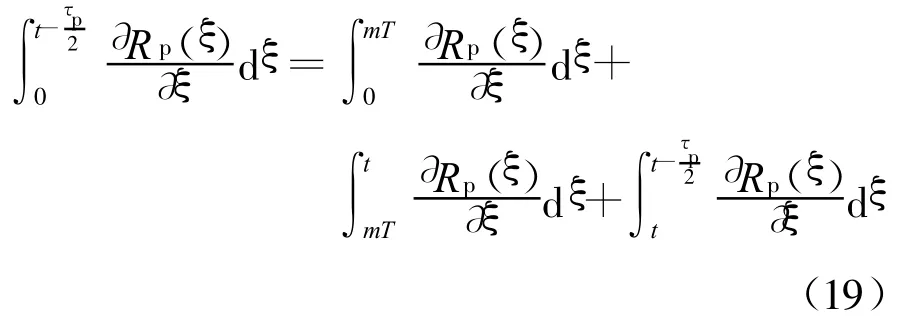
根据积分中值定理

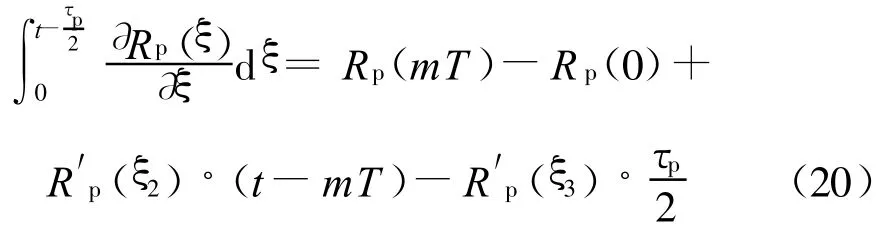
同时,令

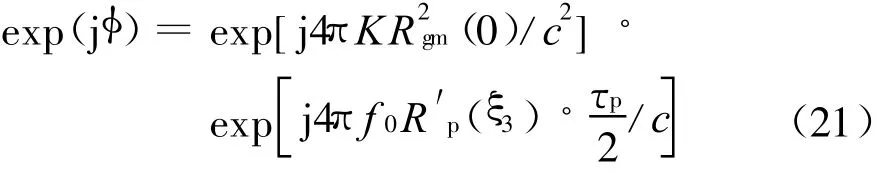
将式(20)、(21)代入式(18)得

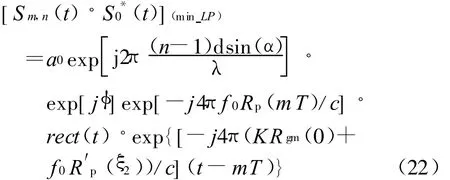
显然,式(21)随时间变化对式(22)的值影响很小,对距离维和多普勒维FFT时可看作是常数项。所谓距离变换是指对式(22)所表达的信号在其中某个扫频周期段上独立做傅立叶变换。对每一个扫频周期段而言,式(22)第三行是一个不变量,实际上起作用的是最后一项,该项是以t-mT为变量的指数函数,只不过它被矩形脉冲rect(t)截断了,所以,t-mT又称为快时间项。相对而言第三行是以mT为变量的函数,称为慢时间项。对式(22)进行傅立叶变换可得

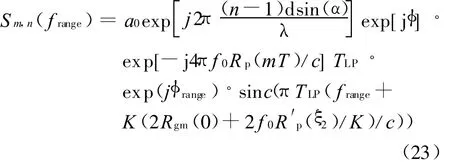
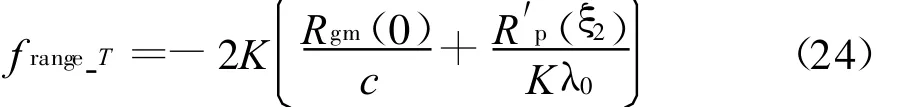
显然,峰值位置主要由回波信号的初始群路径决定,其它均为小量。R′p(ξ2)随时间变量mT可能发生变化,由于它的存在,说明相位路径的变化也会影响距离单元形成上的影响,称为距离、多普勒耦合。

3.2 方位维回波信号处理表达式推导

考虑电离层空间不均匀特性,到达不同天线单元回波信号相位路径除阵元间距引起的差别外,还存在附加相位路径差ΔR pn1(MT):

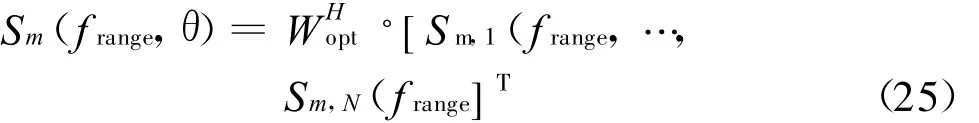
令

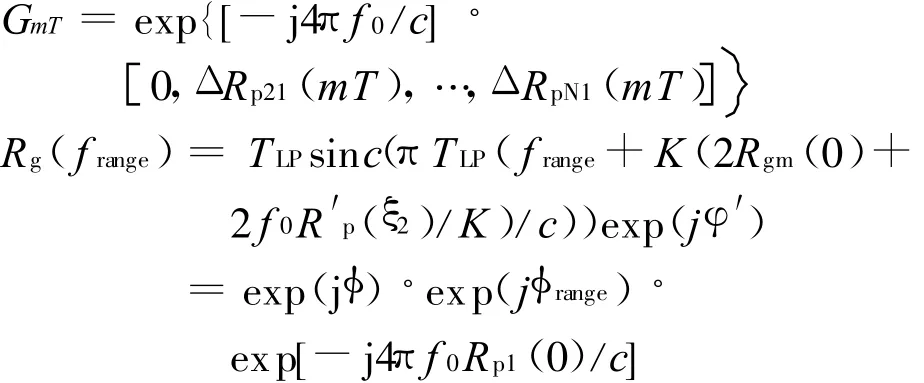
代入式(25)得

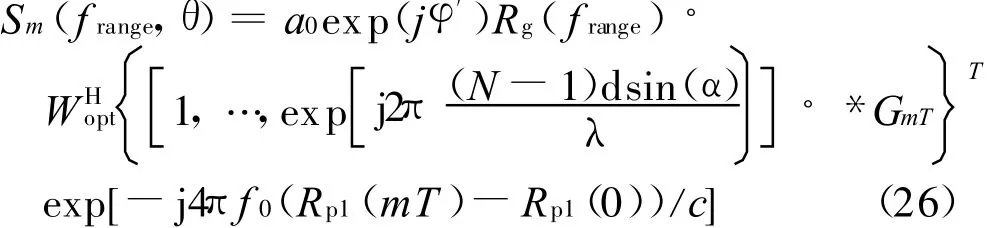
考虑波束形成在其中某个扫频周期段上独立进行,不考虑时间因子mT的影响。从式(26)第二行中可看出,由于电离层空间的不均匀性,使得GmT不为全1向量,各天线阵子间产生了附加的波程差,引起了波束指向变化和展宽。

3.3 多普勒维回波信号处理表达式推导

令

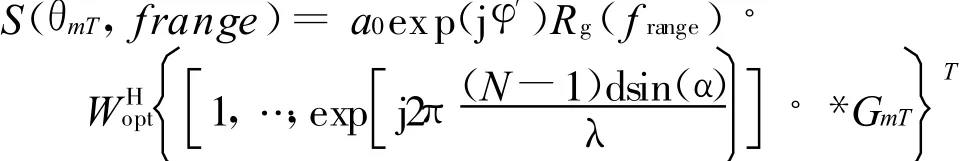
则

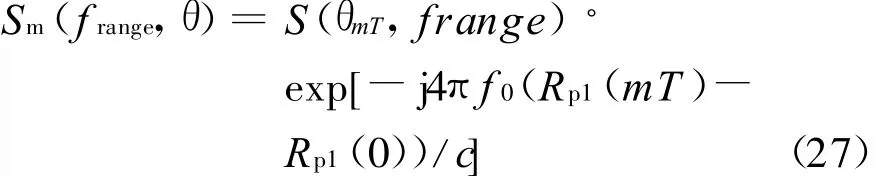
相位路径的变化可以认为由目标运动和电离层变化两部分引起,即

式中:ΔR pv(mT)表示目标运动引起的相位路径变化;ΔR p(mT)表示电离层时变引起的相位路径变化。考虑目标径向匀速运动,运动速度为νr,则式(28)可写为

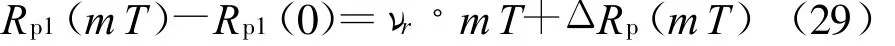
对式(27)在慢时间因子mT上作傅立叶变换,完成多普勒处理。

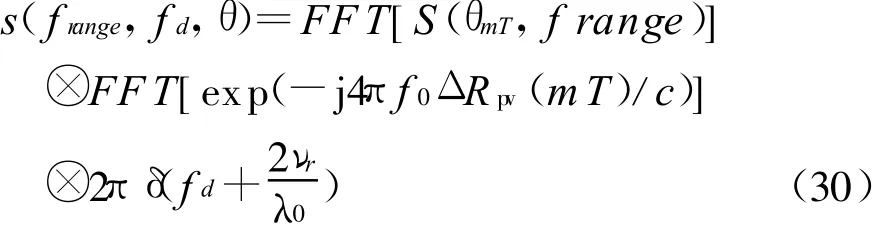
不考虑 FFT[S(θmT,f range)]项,对式(30)分三种情况进行分析:

1)不考虑电离层影响

fd仅由目标运动引起的相路径变化决定,多普勒频移 fd=-2νr/λ0。

2)电离层引起相位路径线性变化

f d由目标和电离层运动引起的相路径变化共同决定,由于电离层引起相路径变化为线性,可设

式中,R′p表示电离层引起的相位路径线性变化率。此时多普勒频移

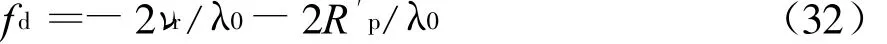
3)电离层引起相位路径非线性变化

f d由目标和电离层运动引起的相路径变化共同决定,且由于电离层引起相路径变化为非线性,将不只引起多普勒频移,还形成一定的频谱展宽,其展宽程度取决于相位路径的非线性变化率。

单独对FFT[S(θmT,f range)]项进行分析:

1)不考虑电离层空间差异

2)仅考虑电离层空间差异

3)同时考虑电离层空间差异及差异时变特性

还有一点需要说明,在多普勤维推导中没有考虑群路径变化对多普勒的影响,从前面的分析可看出:群路径变化对多普勒影响非常小,可忽略不计。

4.仿真验证

根据前面的理论推导可以看出,电离层相位路径变化会引起距离-多普勒耦合,这类问题已在常规雷达中成功解决,技术较为成熟,因此,本文不再对距离维处理和解耦合进行仿真论述。

以美国的OTH-B雷达系统为例,进行电离层存在空间不均匀特性下的波束形成仿真。OTH-B雷达系统接收阵列采用三种不同的接收孔径,通过从247个阵元的全天线阵中选取83个等间距单极子阵元子集实现。表1给出了接收阵列频率切换和相应的阵列孔径。

表1 接收阵列频率切换和阵列孔径

仿真中工作频率 f为20 MHz,阵元间距d为6.1 m,阵元个数N为83。图2中实线图形为波束指向0度时(即阵列法线方向)数字波束形成的方向图,为了压低副瓣,添加了40 dB的切比雪夫窗函数。添加如式(33)所示的正弦空间相位污染曲线,模拟电离层引起的空间相位变化。

式中:0≤n≤N;g0为常数幅度因子β为调制指数;γ为正弦调制频率;λ为工作波长。本次仿真参数取g0=1;β=2π;γ=0.01。

图2中虚线为添加空间相位变化曲线后的方向图,显然,波束指向发生变化,主瓣宽度明显展宽,副瓣抬高。将解时变相位污染的相位梯度自聚焦(PGA)算法引入空间相位污染抑制中,如图3所示,显然空间相位污染得到了很好的抑制,波束明显锐化,指向得到校正,副瓣下降。

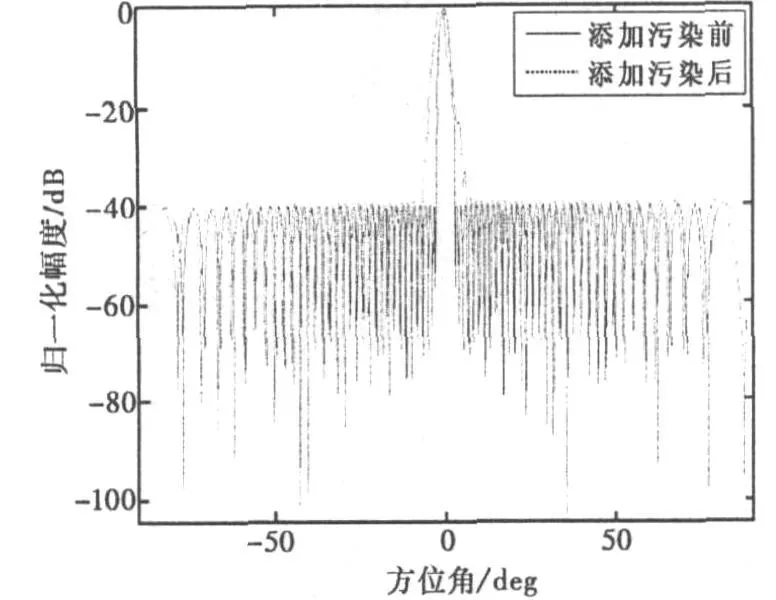
图2 添加空间相位污染前后波束形成比较

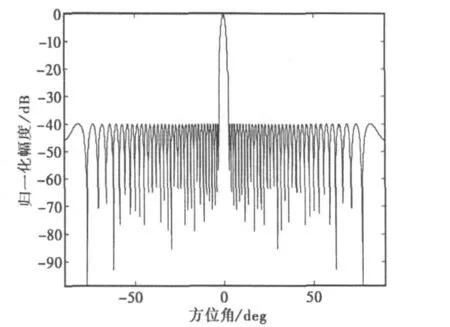
图3 解空间相位污染后波束方向图

时变电离层相位污染的仿真与抑制,已经有多篇文献讨论,不再展开论述。

5.应用实例

高频地表面波雷达(HFSWR)与天波海态雷达工作在相同频段,杂波谱结构类似,差别在于HFSWR没有电离层相位污染,人为地添加相位扰动可便于比较算法校正前后的效果。采用某地波雷达实验数据,工作频率为7.5 MHz,脉冲重复周期为0.7264秒,相干积累时间为371.9秒。某一个海面单元散射的回波功率谱如图4所示,两个强大的一阶Bragg峰非常突出,位于约-0.34 Hz处的目标信号也清晰可见。人为添加相位污染曲线,受到污染后的信号功率谱如图5所示。显然,在图5中目标信号和海杂波均被大幅度展宽,无法准确提取海杂波参数,同时目标信号已无法分辨。采用PGA相位估计算法进行校正。图6(b)给出了添加污染曲线和估计曲线的对比图形,校正后的回波功率谱如图6(a)所示。从该图可看出,经过校正处理后,污染回波功率谱得到了锐化,目标信号清晰重现。

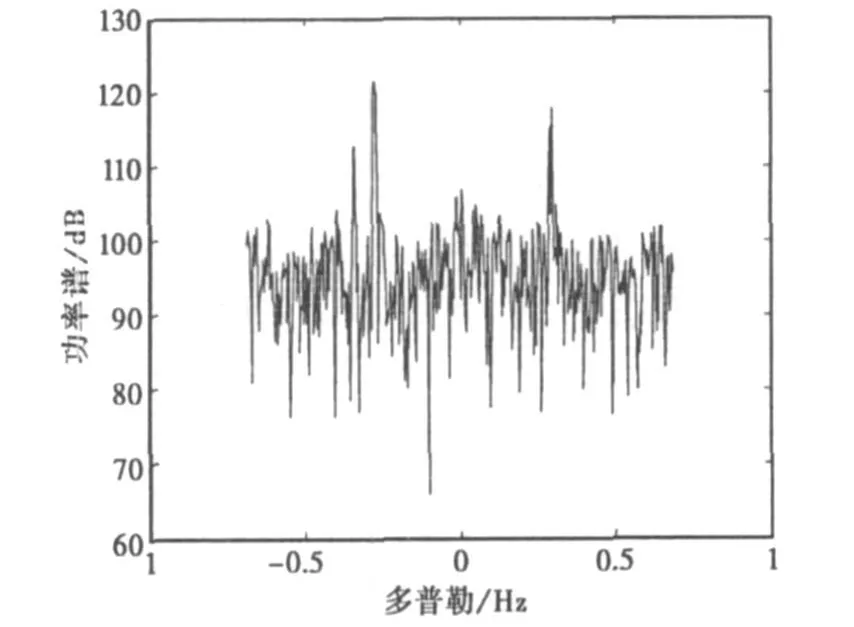
图4 某地波雷达频谱

6.结 论

电离层空时相位随机变化特性使天波海态雷达方位波束宽度、杂波频谱展宽,降低雷达方位分辨率和频谱分辨率,影响风速、风向、浪高谱等海杂波参数反演精度,需要对其进行有效地抑制。部分解时变相位污染算法可应用于空间相位污染。通常,首先进行空间相位污染抑制,数字波束形成,然后再进行时间相位污染抑制,最终进行多普勒处理,这样雷达方位分辨率和多普勒分辨率会大大提高。

[1] GEORGEST M,HARLAN J A,LEBEN R R,et al.A test of ocean surface current mapping with over-thehorizon radar[J].IEEE Trans.Geosci.Remote Sense,1998,36(1):101-110.

[2] AHEARN JL.Tests of remote skywavemeasurement of ocean suface conditions[J].Proceedings of The IEEE,1974,62(6):681-687.

[3] GEORGES T.M.Progress Toward a Practical Skywave Sea-State Radar[J].IEEE Transactions on antennas and propagation,1980,28(6):751-761.

[4] 杨志群.天波海态雷达信号处理方法研究[D].南京理工大学博士学位论文,2003

[5] 孙广俊,齐东玉,李铁成.利用返回散射系统监测海洋回波[J].电子学报,2005,33(7):1334-1337.

SUN Guangjun,QI Dongyu,LI Tiecheng.Sea echo detection using ionosphere backscatter sounding system[J].Acta Electronica Sinica,2005,33(7):1334-1337.(in Chinese)

[6] 韩蕴洁,杨志群,储晓彬.天波雷达检测舰船时电离层失真的校正方法研究[J].现代雷达,2003,25(10):5-8.

HAN Yunjie,YANG Zhiqun,CHU Xiaoshan.Research on the correction of ionospheric distortion for ship detection in OTHR[J].Modern Radar,2003,25(10):5-8.(in Chinese)

[7] BOURDILLON A,GAUTHIER F,PARENT J.Use of maximum entropy spectral analysis to improve ship detection by over-the-horizon radar[J].Radio Science,1987,22(2):313-320.

[8] 邢孟道,保 铮.电离层电波传播相位污染校正[J].电波科学学报,2002,17(2):129-133.

XING Mengdao,BAO Zheng.Phase perturbation correction of radiowave propagation in ionosphere[J].Chinese Journal of Radio Science,2002,17(2):129-133.(in Chinese)

[9] HOWLAND P E,COOPER D C.Use of the Wigner-Ville distribution to compensate for ionospheric layer movement in high-frequency sky-wave radar systems[J].IEEE Proceedings-F,1993,140(1):29-36.

[10]ANDERSON S J,ABRAMOVICH Y I.A unified approach to detection,classification,and correction of ionospheric distortion in HF sky wave radar systems[J].Radio Science,1998,33(4):1055-1067.

[11] LU Kun,WANG Jiong,LIU Xingzhao.A piecewise parametric method based on polynomial phase model to compensate ionospheric phase contamination[C]//Proc.of ICASSP'03,HongKong,China,2003:405-409.

[12] 李 雪,邓维波,焦培南.分段多项式建模解电离层慢径相位污染阶数选择新方法[J].电波科学学报,2009,24(6):1-6.

LI Xue,DENG Weibo,JIAO Peinan.A New order-select method of polynomial modeling for Ionosphere phase perturbation correction[J].Chinese Journal of Radio Science,2009,24(6):1-6.(in Chinese)

[13] 姬勇力,江长荫.返回散射回波去电离层相位污染方法比较和分析[J].电波科学学报,2008,23(3):484-490.

JI Yongli,JIANG Changyin.Comparison and anyalysis of ionospheric phase decontamination methods for backscattered signals[J].Chinese Journal of Radio Science,2008,23(3):484-490.(in Chinese)

[14] DAVICESK.Ionospheric Radio[M].Peter Peregrinus Ltd.,London,1990.