MLFMA用于直升机多普勒回波信号仿真

向道朴 周东明 何建国

(国防科技大学电子科学与工程学院,湖南长沙410073)

1.引 言

雷达回波数值模拟在雷达系统的设计、研制和测试阶段发挥着十分重要的作用,它使得雷达设计师可以在一种近似实物仿真的条件下来分析雷达系统的性能。对运动目标雷达回波模拟,最常用的方法是将目标等效成点目标及其组合,用点目标回波模拟运动目标回波。具有运动部件的目标,如直升机主旋翼和尾翼、螺旋桨飞机的螺旋桨以及喷气式飞机的涡轮机叶片等,对雷达入射波产生周期性的调制会导致回波频谱展宽[1]。文献[1][2][3]从信号处理的角度提出将直升机主旋翼桨叶等效成线状散射体,该计算模型认为直升机主旋翼总的回波为单个桨叶回波信号的简单叠加,这一简化模型正确给出了直升机雷达回波“闪烁”出现的时刻及回波包络,被众多学者用来验证识别直升机的各种算法[2-4]。不过该模型过于简单,存在诸多不足:首先,实际的直升机主旋翼,具有复杂的流线型物理结构,桨叶前后沿不对称,前后沿RCS相差约5 dB;其次,直升机的主旋翼是紧贴在机身上的,在雷达波束照射下,机身回波和主旋翼回波之间存在多次反射且相互影响,不能仅以独立存在的旋翼来计算回波。

矩量法及其快速算法,能对任意形状目标的散射场进行精确计算,其结果考虑了模型各部分之间的相互影响,被公认为是最精确的数值解。不过现有的软件包,只能处理静止目标在电磁波照射下产生的散射场,不能处理运动目标在电磁波照射下产生的散射场。本文提出一种应用准静态技术结合多层快速多级子算法模拟运动直升机在电磁波照射下产生的多普勒回波的方法[5],并用高分辨时频分布算法对仿真得到的运动直升机的多普勒回波进行分析,从中提取出直升机旋翼细节信息,并与文献[3]中基于线型模型得到的直升机回波信号的结果进行了对比,结果表明,本文提出的方法由于考虑了直升机旋翼与机身的相互影响,模拟得到的直升机多普勒回波信号包含丰富的时变谱信息,可以推测,应用准静态技术结合多层快速多极子算法模拟得到的直升机多普勒回波更加真实,非常适合用于验证直升机目标识别算法。

2.基本原理

应用准静态技术结合多层快速多极子算法计算直升机多普勒回波的物理依据是:一切宏观运动的速度相对光速而言都是极其微小的;时谐电磁波照射运动目标,在目标表面感应出时谐电流,认定某一观测时刻目标表面电流在该时刻已经达到稳定状态不会引起很大的误差。快速多极子算法作为求解电磁场积分方程的快速算法,以未知电流和磁流作为求解对象,非常适合与准静态技术相结合,模拟运动目标引起的微多普勒信号。

时谐电磁场的复数表示式和瞬时表示式之间存在以下关系

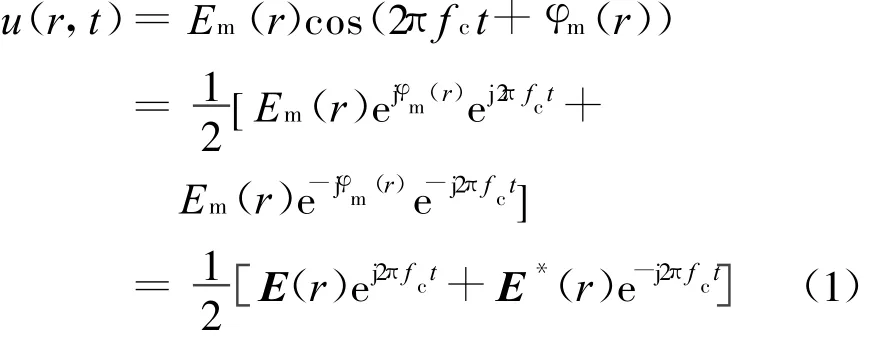
式中:fc为雷达工作频率;φm(r)为初相;Em(r)为振幅;E(r)为复振幅矢量,对应电磁场数值计算中的时谐稳态解。u(r,t)与信号e-j2πfct相乘后得

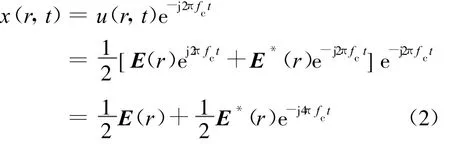
可得到E(r)。

频域多层快速多级子算法求解电磁散射问题将得到时谐稳态解,由式(2)可知,时谐稳态解与实际的连续波零中频雷达正交混频器的输出相对应,本文将利用这种对应关系,应用准静态技术结合多层快速多级子算法,计算直升机多普勒回波信号。

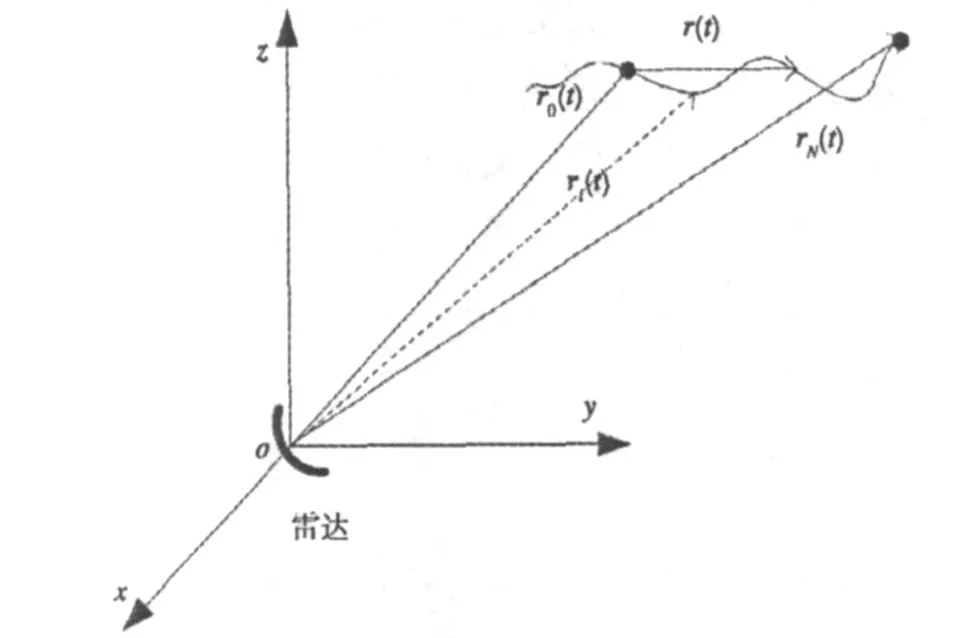
图1 准静态技术示意图

设目标沿图1中曲线所示的轨迹运动。将采样时刻表示为一向量t=[t0,t1,…,t N],设与t相对应的空间位置向量表示为r=[r0,r1,…,r N],雷达接收到的信号为

式中,r(t)为雷达与目标在t时刻时二者之间的距离。xr(r,t)经零中频正交混频后的输出表示为

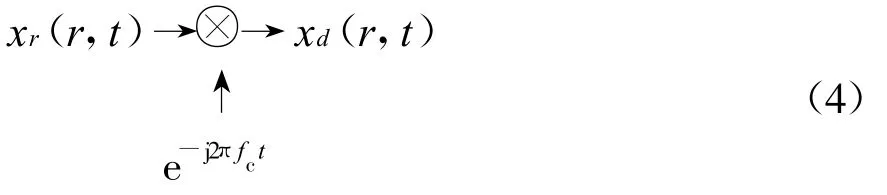
将向量t和r代入式(4)得

有

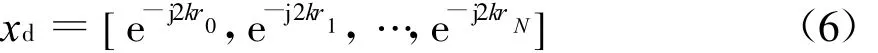
弄清上述基本原理后我们将应用准静态技术结合多层快速多极子算法求解运动目标多普勒回波信号的流程总结如下:

1)设定雷达工作频率 fc,并依据 fc对目标进行剖分,提取目标剖分后的网格数据;

2)构建计算模型,即电磁场积分方程;

4)按目标运动形式对目标网格坐标进行更新,确定下一时刻目标的空间位置;

5)重新计算目标处于新位置的时谐稳态解作为该时刻目标多普勒回波信号;

6)重复4)和5)直到结束。

4)和5)两步具体的计算过程将在第3节详细介绍。

3.直升机多普勒回波信号数值模拟

直升机机身和旋翼运动方式不同,机身一般作平动,旋翼除了平动外还存在转动,应用准静态技术结合多层快速多极子算法计算直升机多普勒回波,如何构建计算模型?如何设定采样方案?如何计算?下面将详细予以讨论。

3.1 模型建立

将机身和主旋翼作为一个整体进行建模并剖分,主旋翼与机身连接处的网格会因主旋翼相对机身旋转而相互错位,导致网格坐标更新后无法基于新的网格数据构建基函数。为了解决这个问题,我们对直升机的主旋翼及机身分别建模,分别剖分,如图2所示,实际计算过程中,通过读取两部分网格数据,每部分网格坐标依据该部分的运动情况进行更新,坐标更新完后将各部分网格数据组合在一起构成一个新的网格数据文件,最后通过对新的网格数据文件进行处理,构造出矩量法及快速算法所需要的基函数,用快速多极子算法进行计算。

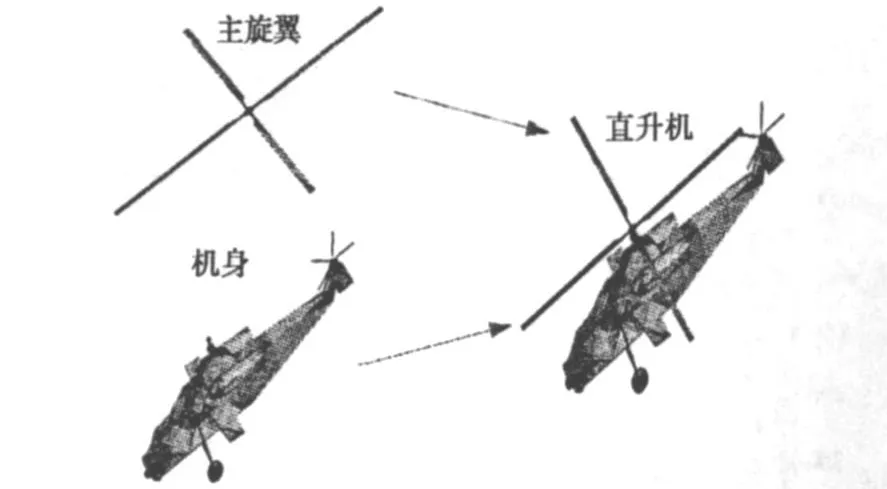
图2 建模示意图

3.2 采样方案设定

直升机多普勒回波频谱是时变的,简单的傅立叶变换不能从多普勒回波中提取出频谱时变信息,高分辨时频分布是动态信号分析的一种有效工具,为了应用高分辨时频分布分析动态信号,要求对信号的采样率不低于信号最高频率的4倍[10]。设直升机主旋翼因旋转而产生的最大多普勒频移为fdmax,为了保证高分辨时频分布不产生混叠,要求采样率f s≥4f dmax。采样率确定后通过给定多普勒谱分辨率Δf就可确定需要的采样点数

式中,N即为需要的采样点数。仿真结束后应用核加窗Cohen类高分辨时频分布算法对模拟得到的多普勒回波信号进行处理,即可从中提取出主旋翼运动信息。

3.3 计算

在准静态假设条件下,各个采样时刻处理的是静止目标电磁散射问题,不同时刻模型网格由初始时刻网格通过坐标变换得到。多层快速多级子算法求解静止目标的散射场最终归结为求解线性方程组[7-9],其矩阵形式为[Z][I]=[V],其中[Z]为阻抗矩阵,[I]为电流系数向量,[V]为激励向量。阻抗矩阵[Z]表征了目标表面各离散单元之间的相互作用,不同时刻目标相对雷达将有不同的姿态,通过三维坐标变换,某时刻目标的姿态可由初始时刻目标的姿态经坐标变换得到。模型网格数据更新后,重新计算出阻抗矩阵[Z]和激励向量[V]并求解[Z][I]=[V],得到新时刻的电流[I],由电流[I]计算出远场并记录各个时刻的远场数据即得运动目标多普勒回波信号。

4.基于核加窗高分辨时频分布的多普勒特征提取

信号s(t)的核加窗Cohen类时频分布可表达为

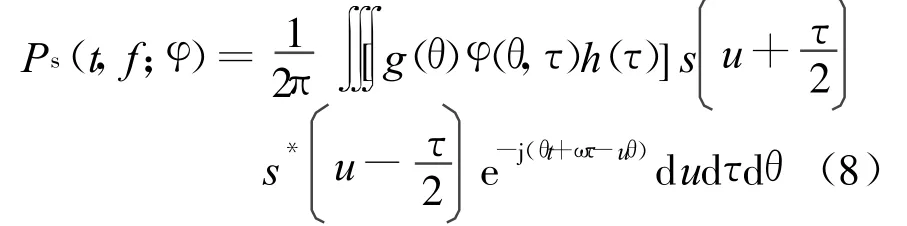
式中,g(θ)与h(τ)分别为频域平滑窗和时域平滑窗,选取适当的窗函数对核函数进行加权,然后对信号s(t)的Wigner-Ville分布进行二维滤波处理,从而有效抑制交叉项,又尽可能保留Wigner-Ville分布高时频分辨率的优点[10]。

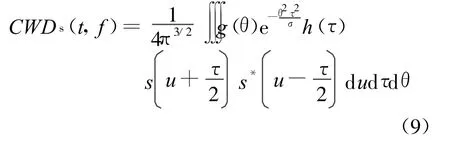
将s(t)离散得到一序列,记为z(m),(1≤m≤N),其中N为序列长度,信号z(m)的瞬时自相关矩阵RN×N为

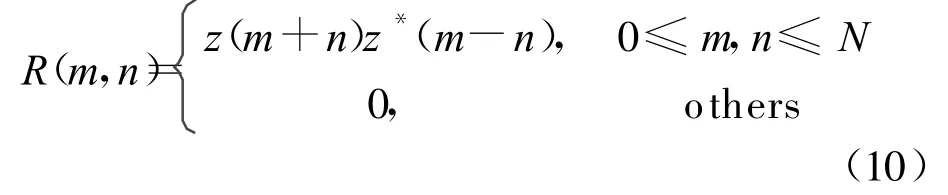
离散核加窗Choi-Williams分布为

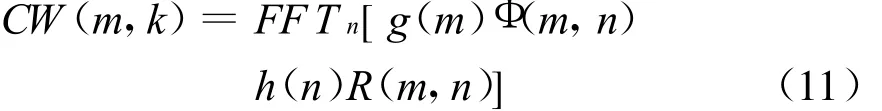
式中:FFT n[·]指对n的快速傅立叶变换;g(m)为对频率m的平滑窗,计算过程中取 g(m)为9点Kaiser窗;h(n)为对时间n的平滑窗,计算过程中h(n)为63点 Kaiser窗;Φ(m,n)为核函数 Φ(p,q)=的二维离散傅立叶变换。时频分布在时频面内的投影即为瞬时频率曲线,实际的时频分布由于测不准原理的限制,不能同时达到时间与频率聚焦。

5.数值结果与讨论

为了验证准静态技术结合快速多极子计算直升机多普勒回波的有效性,将应用两个算例给出文献中从信号处理的角度基于线型模型模拟的直升机多普勒回波[2-3](线型模型信号)与应用准静态技术结合快速多极子算法计算得到的直升机多普勒回波(计算模型信号)经时频分布处理后的结果,并进行比较。

算例1为四桨叶武装直升机模型——南非“茶隼”武装直升机模型CSH-2,CSH-2机长18.73 m(主旋翼与尾翼非折叠);主旋翼直径L=15.58 m,四桨叶;尾翼直径2.77 m,5桨叶;机高5.19 m。设主旋翼转动频率为 frot=6转/秒,雷达工作频率为200 MHz(波长λ=1.5 m,最大网格尺寸不超过λ/10,雷达与直升机模型相距300 m,计算过程中旋翼和机身分别共剖分成24704和6144个三角形面元。主旋翼旋转引起的最大多普勒频率为

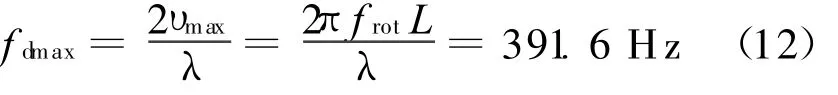
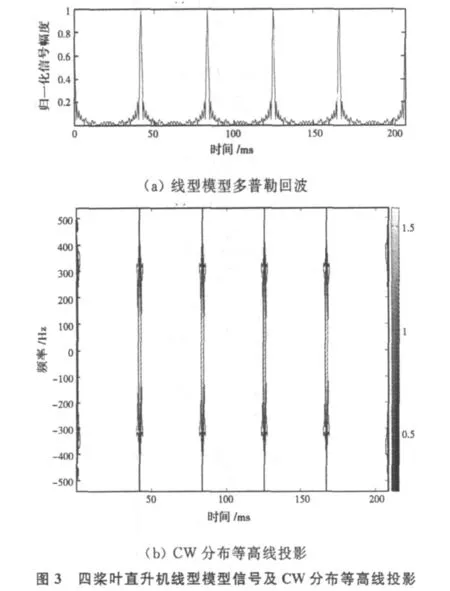
为了便于处理,将两种回波数据关于各自的最大值进行归一化,基于线型模型模拟得到的“茶隼”武装直升机多普勒回波信号及CW分布等高线的投影如图3所示,应用准静态技术结合快速多极子算法计算得到的“茶隼”武装直升机多普勒回波数据及CW分布等高线的投影如图4所示。

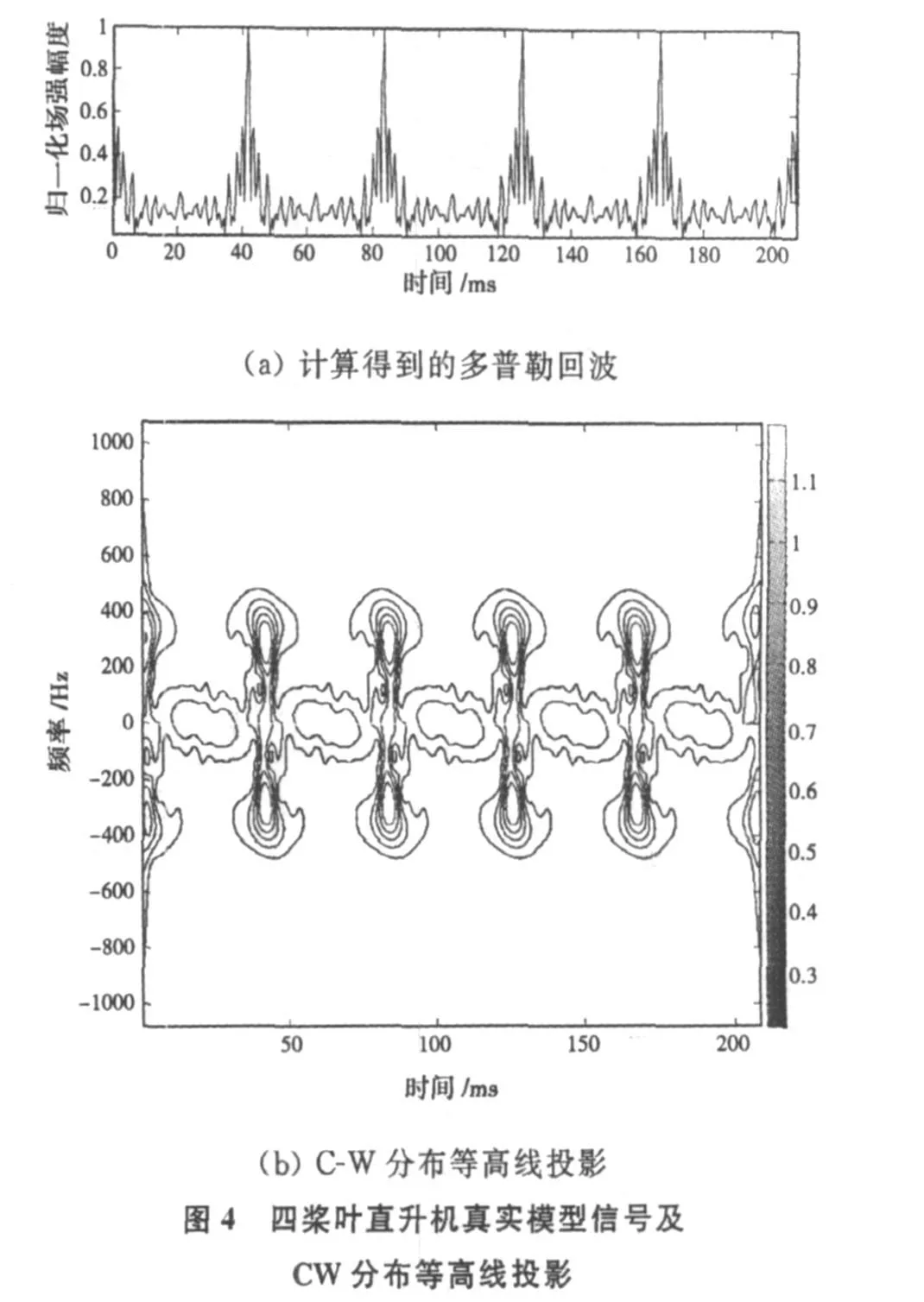
算例2为三桨叶直升机模型(去掉四桨叶“茶隼”武装直升机模型中的一桨叶并将剩下的三桨叶重排成实际三桨叶武装直升机主旋翼形式后得到),其他设置与算例1相同,其中三桨叶旋翼被剖分成4688个三角形面元,机身单元数与算例1相同。

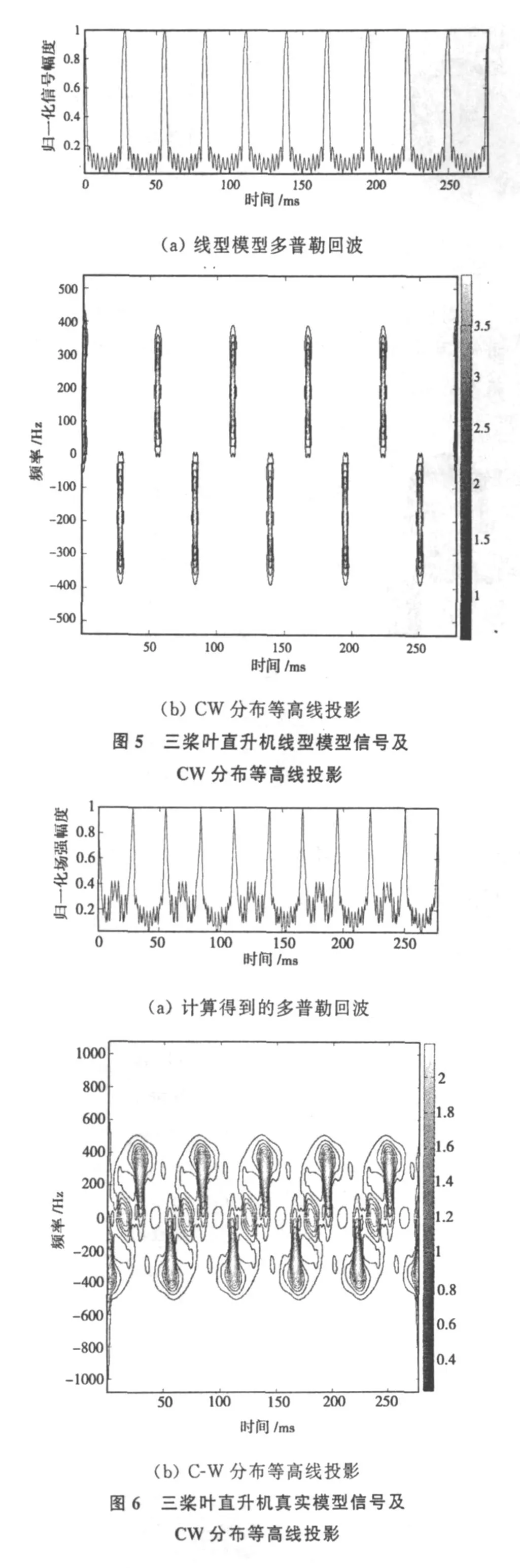
基于线型模型模拟得到的“三桨叶”武装直升机多普勒回波信号及CW分布等高线的投影如图5所示,应用准静态技术结合快速多极子算法计算得到的“茶隼”武装直升机多普勒回波数据及CW分布等高线的投影如图6所示。由图3、图4、图5和图6可以看出,考虑直升机机身与旋翼之间相互作用后得到的直升机多普勒回波信号包含丰富的时变谱信息,这些信息将有助于对直升机目标的识别。

设直升机主旋翼桨叶数为N,从上面两个算例可以看出,当N为偶数时,旋翼闪烁频率为旋翼转动频率的N倍,偶数桨叶具有对称双边频谱;当 N为奇数时,旋翼闪烁频率为旋翼转动频率的2N倍,奇数桨叶正负谱区不对称且正负谱区交替出现,这与文献[4]中由实测得出的结论是一样的。

6.结 论

雷达回波数值模拟,具有重要的工程应用价值。数值模拟的关键在于建立与实际相符的计算模型,本文应用准静态技术结合快速多极子算法,成功模拟了运动直升机多普勒回波信号,并应用高分辨时频分布算法对模拟得到的多普勒回波信号进行了分析,提取出了直升机旋翼桨叶细节信息。仿真结果表明:本文提出的方法模拟的直升机多普勒回波信号,由于考虑了直升机的结构细节,可以认为是真实的多普勒回波信号,可直接用于验证直升机各种识别算法的性能。

[1] CHEN V C.Radar signatures of rotor blades[C]//Proceedings of SPIE on Radar Processing.Orlando,FL,USA,2001,4391:63-70.

[2] 汤子跃,王永良,蒋兴舟.相控阵机载预警雷达对悬停直升机的探测[J].电子学报,2001,29(9):1249-1252.

TANG Ziyue,WANG Yongliang,JIANG Xingzhou.Study on the detection method of hovering helicopter target with phased array airborne early warming radar[J].Acta Electronica Sinica,2001,29(9):1249-1252.(in Chinese)

[3] 孙文峰,张 晨,王永良.悬停直升机雷达探测技术[J].电子学报,2002,30(6):896-899.

SUN Wenfeng,ZHANG Chen,WANG Yongliang.Radar detection of hovering helicopter[J].Acta Electronica Sinica,2002,30(6):896-899.(in Chinese)

[4] 郗 莹,李道京,吕 杨,等.直升机信号的采集与分析[J].雷达与对抗,1999,19(4):33-36.

XI Ying,LI Daojing,LV Yang,et al.Helicopter signal acquisition and analysis[J].Radar and Ecm,1999,19(4):33-36.(in Chinese)

[5] COPPLERJ.Scattering by moving bodies:the quasistationary approximation[J].Mathematical Methodsin Applied Sciences,1980,2(2):131-148.

[6] MARTIN J,MULGREW B.Analysis of the theoretical radar return signal f rom aircraft propeller bladders[C]//IEEE International Radar Conference.Washington DC,USA,1990:569-672.

[7] 胡 俊,聂在平,王 军,等.三维电大目标散射求解的多层快速多极子方法[J].电波科学学报,2004,19(5):509-514.

HU Jun,NIE Zaiping,WANG Jun,et al.Multilevel fast multipole algorithm for solving scattering from 3-D electrically large object[J].Chinese Journal of Radio Science,2004,19(5):509-514.(in Chinese)

[8] 袁 军,邱 扬,刘其中,等.自适应多层快速多极子算法及其并行算法[J].电波科学学报,2008,23(3):455-459.

YUAN Jun,QIU Yang,LIU Qizhong.Adaptivemultilevel fast multipole algorithm and its parallel algorithm[J].Chinese Journal of Radio Science,2008,23(3):455-459.(in Chinese)

[9] 樊振宏,丁大志,陈如山.多层快速多极子技术分析微带天线[J].电波科学学报,2008,23(2):235-238.

FAN Zhenhong,DING Dazhi,CHEN Rushan.Multilevel fast multipole approach for analysis of microstrip antennas[J].Chinese Journal of Radio Science,2008,23(2):235-238.(in Chinese)

[10] 科恩L.时频分析:理论与应用[M].西安交通大学出版社,1998.

COHEN L.Time Frequency Analysis:Theory and Application[M].Xi'an Jiaotong University Press,1998.(in Chinese)