基于PNA多通道扫频近场测量速度与精度分析

李 勇 李焱明 傅德民 于 丁 欧 杰

(西安电子科技大学天线与微波技术国防科技重点实验室,陕西 西安710071)

1.引 言

近场测量技术以其获取信息量大、所需场地小、可全天候工作、环境影响小以及安全保密等一系列优点,在现代天线测试中获得了广泛的应用,已被IEEE指定为标准测量方法[1]。由于近场测量是用特性已知的探头在包围待测天线的某一几何表面进行扫描,通过采样均匀网格点上的幅相数据进行近远场变换求得天线远场辐射特性的方法。该方法扫描(机械或电扫描)过程需要一定的时间,而且传统的近场测量一次扫描仅能测得单一频点的数据。

现代相控阵天线、宽带天线和多通道天线的发展,要求对天线进行多波束、多频点和多通道的测量,以全面检定天线的辐射特性,这对近场方法提出了严峻的挑战,迫切需要提高近场测量的效率。本文基于Agilent新型矢量网络分析仪PNA,研究了多通道扫频近场测量系统的特性,针对系统的测量速度和精度问题进行了详细的分析讨论,并对系统的动态范围、接收机的幅相漂移、测量的位置误差等主要误差源进行了分析,给出了提高测量精度的方法[2]。

2.PNA特点与近场测量系统配置

网络分析仪作为全面测定网络参数的仪器,从1985年有公司创造性地将其用于天线和RCS(Radar Cross Section)测试开始,至今这种卓越的新技术已经演变成天线和RCS测量的专用微波接收机。Agilent新推出的PNA系列网络分析仪,具有高速度和高精度特性,能够满足现代复杂天线的多功能测试需求,通过提供快扫描速度、宽动态范围、低迹线噪声和灵活的连接能力,为天线和RCS测量提供了有力的技术保障。

接收机的中频带宽IFBW(Intermedial F-reguency Bandwidth)影响着接收机的测量精度和灵敏度。以10 kHz IFBW为例,PNA(带有选件014)的灵敏度为-104 dBm,优于通常 8530A/8511,8720等系统6～14 d Bm。PNA的测量速度为20μs(40 k Hz IFBW)和119μs(10 kHz IFBW),明显快于8530A的200μs的数据采集时间。当近场测试范围较大或进行远场配置时,需增加外部信号源,此时PNA的频率捷变时间为4～6 ms,比85301B系统的6～8 ms快25%～33%。为进一步提高性能,PNA也可以采用外混频配置,此时系统的动态范围、压缩电平、混频器匹配、隔离度等指标均与85301B一致。PNA提供29种IFBW选择,使得用户可以根据不同的应用和测试需求对系统的灵敏度和测试速度进行优化。

近场测量属于数据密集型采集,PNA的大数据存储能力与快速传输性能相结合的功能,解决了数据量大的难题。为缓冲和传输数据,PNA最多提供16条通道,每条通道数据容量为16001个数据点。采用基于LAN的DCOM快速数据传输方式,可在2 ms内完成1601个数据点的传输,在121 ms内完成16001个点的数据传输任务。对近场测量可以在整个扫描完成后进行数据传输,也可在每行扫描完成后传输数据。

PNA提供的扫描模式,允许用户以升序、降序或任意和随机跳频进行扫描。尤其降序的反向扫频功能特别适合于近场扫频测量。近场扫描过程中,在探头移动的一个方向上,PNA可以从F1扫描到Fn;当探头反向时,为保证采样网格点的对应关系,频率应从Fn扫描到F1。从而实现了近场扫频测量的双向扫描,最大限度地降低数据采集和扫描时间。

PNA接收机具有四个内置测试接收机(A,B,R1,R2),在无需配置外部PIN开关的情况下,可以同时测量最多三条测试通道(或天线端口),即PNA可以在一个数据采集周期中同时测量A/R1、B/R1和R2/R1。以单脉冲天线为例,对于和支路、方位差以及俯仰差三个测试端口,可以在一个采集周期内完成数据的采集功能,明显地降低了数据采集时间。采用PNA的典型近场测量系统配置如图1。

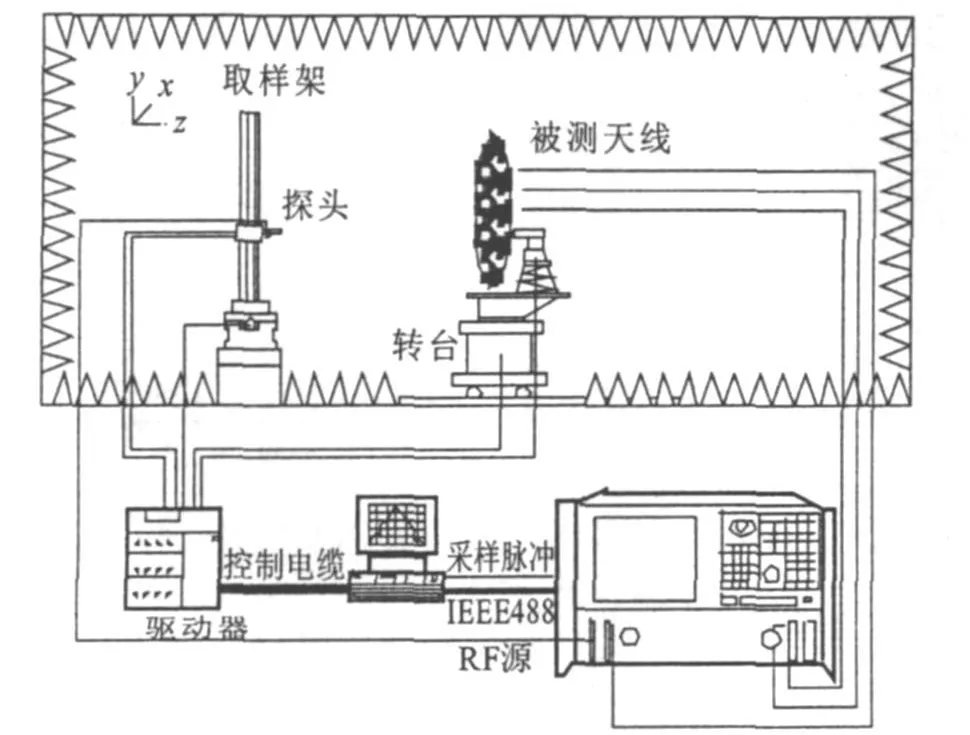
图1 PNA典型近场测量系统配置

从配置中看出AUT的三个端口被直接连到接收机,并同时进行测量。对于X波段阵列脉冲天线,假设有32个波束状态、3个端口、1个极化状态和5个频率点,近场扫描网格为101×101,则每个网格点采集的数据点数为:(天线端口数)×(极化数)×(波束状态数)×(频率点数),即3×1×32×5=480。PNA可以在38 ms内完成480个点的测量。每个数据点的平均采集时间79μs。PNA的测量时间计算包括采集时间、频率转换时间、回扫时间和分析仪开销时间。对于上述测试方案,PNA完成所有网格点扫描时间为7 min,该速度是85301B天线测试系统的2到5倍。若探头的扫描速度为12 cm/s,采样间隔15 mm,完成一遍扫描的时间为21 min,因此,对于简单的测量方案,探头的最大扫描速度,往往是决定总测量时间的关键因素[3]。

3.提高系统精度方法

精度和速度是近场测量的关键指标,如何在快速测量的同时,保证系统的测量精度,是需要我们认真研究的问题。

3.1 动态范围

网络分析仪达到最大的动态范围,对于检测微波器件的特性和超低副瓣天线测试非常重要,以至成为确定测试性能的关键因素。为保证测量系统具有最大的动态范围,有必要了解动态范围的基本概念和提高动态范围的方法[4]。设Pmax为满足误差要求的最大输入功率电平,它的取值决定于接收机的饱和压缩电平;Psig为测试端口的实际功率电平,测试系统设计时,我们希望Psig尽可能接近Pmax;Pmin为系统能够检测到的最小功率电平(灵敏度),由接收机的噪声电平决定。接收机的动态范围定义为:Drec=Pmax-Pmin,而测试系统的动态范围定义为:Dsys=Psig-Pmin。噪声电平是决定动态范围的重要参数,通常使用RMS值定义噪声电平。噪声电平决定了仪器所能测量的最小功率电平,该电平限制了系统的动态范围。噪声电平可以通过平均或减小IFBW得以改善。由于接收机的噪声电平引起的测量误差是天线测量的重要误差源之一,而该误差对测量不确定性的影响,取决于信号与噪声的比值。动态范围和信噪比定义如图2。通常在平均噪声电平上增加10 dB,来定义峰值噪声电平,确保99.96%的噪声电平低于该峰值电平。峰值噪声电平将用于决定信噪比值。

近场测量探头最大接收幅度信号近似等于

式中:GP、Ga分别为探头和AUT的增益;a0为输入到待测天线端口的功率。

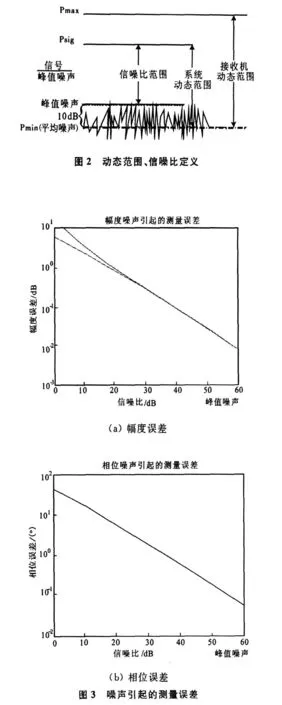
为减小低副瓣测量的噪声影响,由图3噪声引起的幅相误差曲线可知,b0(P)max至少应高于峰值噪声电平50 dB。因而为了保证近场测量的幅度和相位精度,一方面可通过增加a0或探头的增益或二者的组合来达到要求;另一方面,可通过平均或减小IFBW等方法降低系统噪声电平,来增加系统动态范围[5]。

平均功能是降低噪声电平的有效方法之一,付出的代价是增加了测量时间。PNA和其他矢量网络分析仪采用指数权的复数平均,即矢量平均。平均因子每增加一倍,信噪比将增加3 d B,但测量时间也将成倍增加。而改变系统的IFBW将影响接收机数据采集的数字滤波器带宽,通过减小IFBW滤除IFBW外的噪声来降低噪声电平。接收机的轨迹噪声随10倍log(IFBW)而变化,即要降低10 d B噪声电平,需将IFBW减小10倍,接收机的扫描速度与IFBW成反比。图4给出了PNA接收机在四种不同频率(1、3、7、9 GHz)时RMS噪声电平与IFBW关系的试验曲线。表1给出了在10 k Hz快速IFWB情况下,若要降低10 d B或20 d B噪声电平,平均功能或改变IFBW对扫描时间的影响。

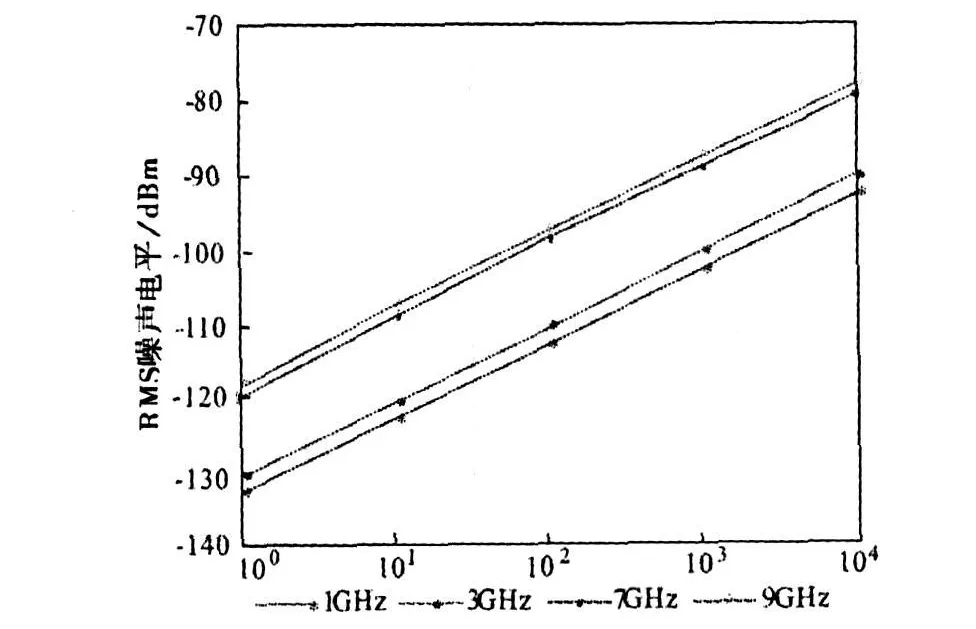
图4 IFBW与噪声电平关系曲线

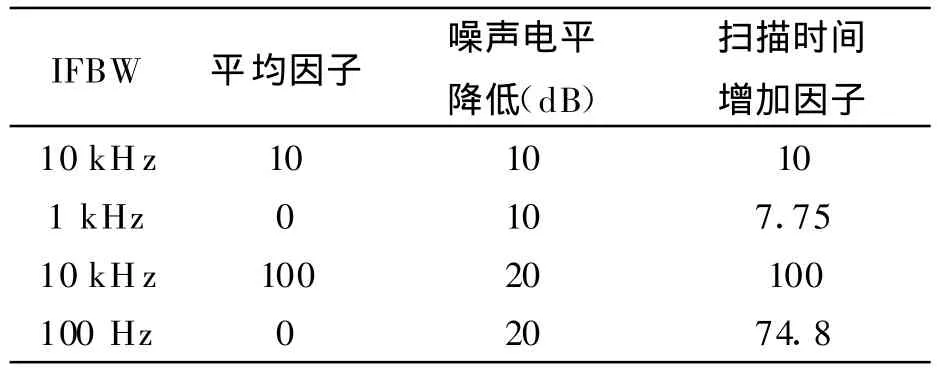
表1 平均功能与IFBW对扫描速度的影响

平均和减小IFBW都能降低系统的噪声电平。平均功能由于要多次采集轨迹数据,并进行修改和显示,因而耗时较多;PNA的多种IFBW选择,为噪声电平的降低和测量速度优化提供了灵活性。总之实际测量时,应根据测量方案合理选择平均因子和IFBW,才能使测试精度和速度得到优化。

3.2 幅相漂移

随着现代仪表技术的发展,接收机和信号源已经具有良好的幅度和相位稳定性,但测量系统中配置的RF电缆,由于暗室环境温度的改变会产生电长度的变化,从而引起接收机幅相信号的漂移。“Tie扫描”已成为克服系统热漂移的标准方法。通常Tie扫描是在近场扫描测量完成后进行。事实上,Tie扫描只是在近场扫描面上预先确定的位置进行一系列附加的测量,以便可以对近场测量数据的不同区域进行相位和幅度的调整。以平面近场测量为例,如果探头的运动方式为沿垂直方向(列)扫描,沿水平方向(行)步进,则对于每一列而言,探头运动的时间相对较短,因而可近似忽略由于接收机的幅相漂移所引入的误差。然而,对于每一行而言,探头由一个取样点运动到另一个取样点所需时间相对较长,尤其是当两个取样点的距离较远时,所需时间则更长。在这种情况下,接收机的幅相漂移便会给近场测量数据引入一定的幅相误差。为了控制和减小这一误差,可以在探头全程扫描结束后,对扫描面上的某一行或多行进行附加扫描测量,进而对近场测量数据进行相位和幅度的修正和调整。

多通道多波束扫频测量时,将间距小于λ/2的主栅格分成S(S=通道数*极化数*波束状态*频率数)个子区间。在双向扫描时,相邻两行的S子区间的扫描顺序是反序的。仍以垂直扫描水平步进为例,扫描时Y轴每个栅格被分成S个子区间进行采样。按常规的Tie扫描方法,在测试扫描完成后,应在扫描面的中间行沿X轴进行附加扫描。由图5可知,Tie扫描将X轴主栅格分成了S个子区间。随着子区间的顺序增加,Tie扫描测试点与近场测试栅格点偏离越来越大,该数据已不能用于近场数据的幅相漂移修正。为解决这一矛盾,使Tie扫描适合于多通道多波束扫频近场测量,我们将Tie扫描与定点监测概念相结合,即定点Tie扫描法。该方法的主要思想是:在近场扫描完成后将探头定位到Tie扫描的位置,对于每个栅格点,分别完成S个状态的测试,测试再步进到下一栅格点,注意在测试过程中探头是静止不动的,从而避免了采样点位置的偏差。

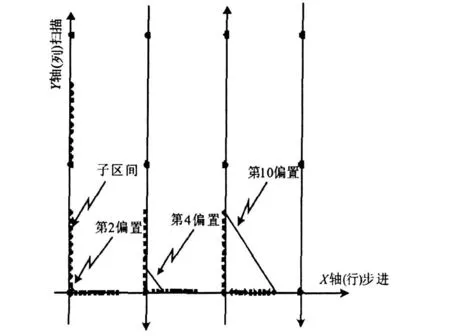
图5 多通道多波束扫频测量X-Y栅格与Tie扫描栅格偏

不失一般性,设近场扫描面共有M行N列(M和N均为奇数),其中第m0行为中心行。对于状态Si探头在扫描面上作全程扫描测量时第m行第n列所对应的取样点处探头的接收信号为bi0(m,n),m=1,2,…,M;n=1,2,…,N;i=1,2,…,S。而定点Tie扫描测量扫描面的中心行(第m0行),对于状态Si设Tie扫描所测得的第n列对应的取样点处探头接收信号为b′i0(m0,n),n=1,2,…,N;i=1,2,…,N;i=1,2,…,S,则修正后第m行第n列所对应的取样点处探头的接收信号b″i0(m,n)为

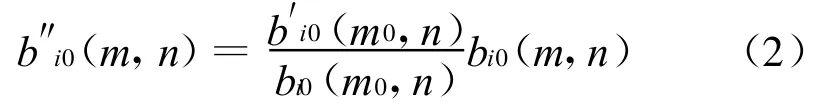
3.3 位置误差

在多通道多波束扫频近场测量中,测量子区间的划分是以采样栅格点为依据的,栅格点的定位精度直接影响近远场变换的精度[6]。从理论上讲FFT变换要求测量均匀间隔的离散栅格点处的场,但实际中由于机械定位精度的限制,必定存在探头位置误差。如果我们能够采用某种算法,在探头位置误差已知的情况下(探头位置误差可由精度更高的激光测量系统确定),由实际测量到的近场幅度和相位恢复出均匀间隔的离散栅格点处场的幅度和相位,然后再进行FFT变换并进行探头补偿,则会提高所得到的天线远场的精度,这一过程便是对探头位置误差进行修正的过程[7-8]。本文所采用的探头位置误差修正算法是插值与迭代相结合的方法。设理论近场栅格点的位置矢为r0,相应的位置误差为δr,首先根据实际测得的电场E(r0+δr),通过插值求得理论近场栅格点r0处的近似电场～Er0;然后由平面波展开理论计算近似平面波谱～A(kx,ky),并进行迭代使～A(k x,k y)逐渐接近于理论平面波谱～A(kx,ky),从而恢复出理想栅格点处的电场E(r0).

由平面波展开理论有

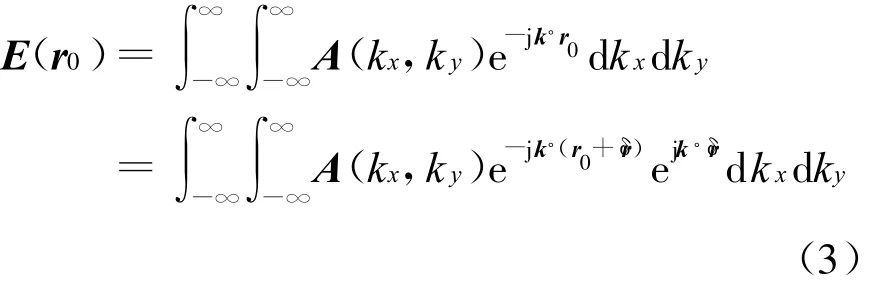
对式(3)中的 ejk·δr进行 Taylor展开 ,有

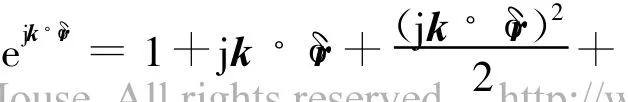
将式(4)代入式(3),得

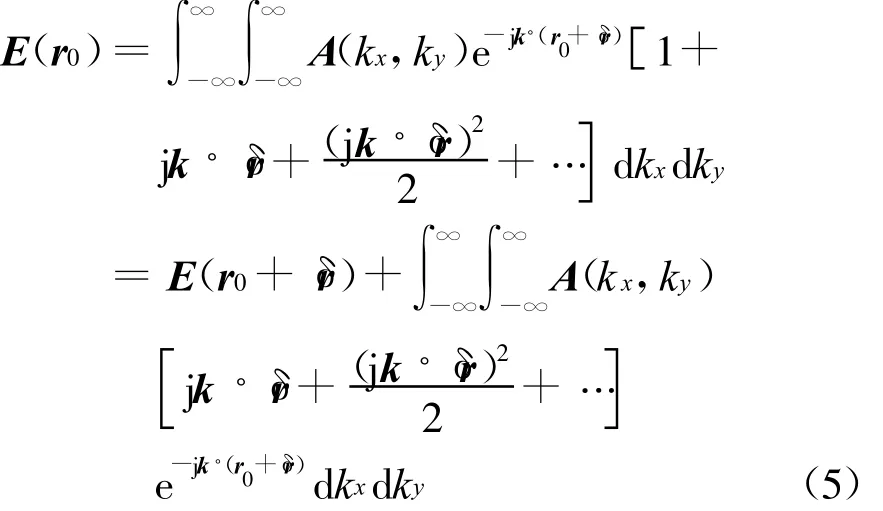
对探头位置误差进行修正的实质就是由实际测得的电场E(r0+δr)恢复出理想栅格点处的电场E(r0).由式(5)不难看出,如果平面波谱A(kx,ky)能够精确求出,那么利用式(5)即可求出理论近场E(r0).算法具体步骤如下:

1)插值处理:为保证对位置误差进行一次修正过程中由实际测量近场得到的近似平面波谱能尽量好地接近理论平面波谱,从而保证求出的一次修正近场能较好地接近理论近场,我们先对实际测得的近场进行插值,由实际测得的近场E(r0+δr)求出理论近场栅格点r0处的近似电场～E(r0).

因为天线产生的电磁场的平面波谱与天线的远场方向图有着直接的对应关系。对窄波束低副瓣天线而言,如果它的最大辐射方向为k0,则在它产生的电磁场的平面波谱中,k0方向的谱含量占绝对优势。作为零阶近似,在分析该天线的近场时,可以认为它是沿k0方向传播的平面波。

如图6所示,过实际近场测量点A作扫描面z=d的垂线,并与扫描面交于B点,过 A点沿-k 0方向作射线与扫描面z=d交于C点。显然r′与r0所对应的点均位于扫描面z=d上。设θ为k 0与扫描面z=d所成的夹角,则由 sinθ=,得 δr′=故有

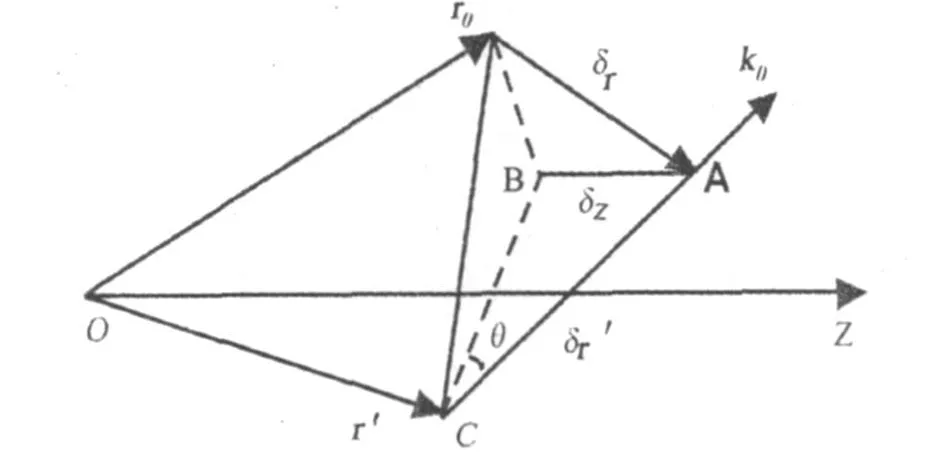
图6 探头位置误差示意图

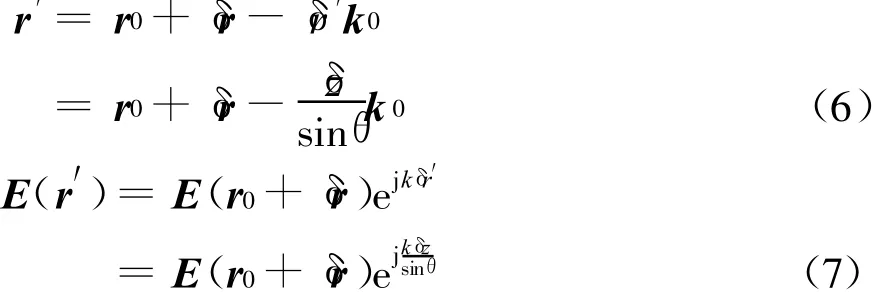
将E(r′)在扫描面z=d上插值,求出理论近场栅格点r 0处的近似电场～E(r 0).

2)由理论近场栅格点r0处的近似电场～E(r0)计算近似平面波谱～A(kx,ky).

由平面波展开理论,有

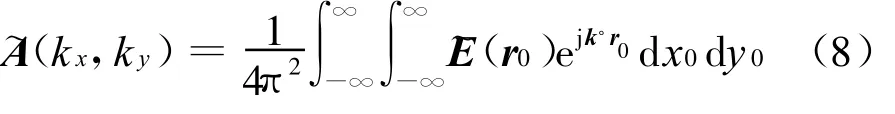
3)用近似平面波谱～A(kx,ky)代替理论平面波谱A(kx,ky),计算式(5)最右边的积分修正项,用～A(k x,k y)代替A(k x,ky),则有

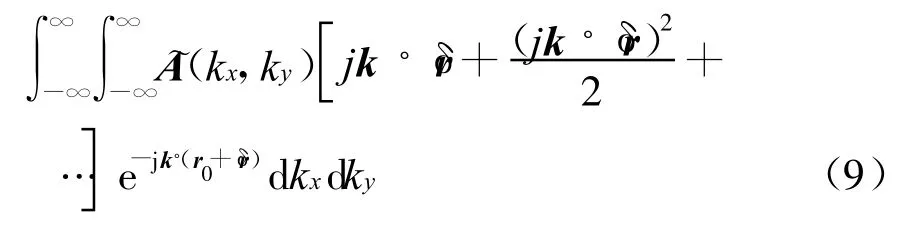
4)求出一次修正近场～E(1)(r0)

将式(9)中所计算的修正项代入式(5),即可求出一次修正近场～E(1)(r0).

5)循环迭代

将所求出的一次修正近场代入式(8),求出近似平面波谱,并用近似平面波谱代替理论平面波谱,由式(9)计算出修正项,最后将求出的修正项代入式(5),即可求得二次修正近场～E(2)(r0).如此反复迭代,即可求得满足精度要求的修正近场。

4.测试实例

根据图1近场测量系统配置,我们对某机载多通道天线进行了扫频测量,测试通道数为3,极化状态为1,频率点数为11。一次扫描完成33个方向图测量。天线口径150 mm×100 mm,频率范围12～18 GHz。采样间隔8 mm(小于频率为18 GHz时的λ/2),取变换后的可信角域为60度,则近场扫描栅格为55×49,扫描面尺寸为440 mm×392 mm;采用垂直扫描水平步进方式,探头的扫描速度设定为100 mm/s,由于受探头起停阶段加速或减速影响,每列实际扫描时间为5 s,水平步进时间为1 s,因而整个近场扫描时间约为5 min。该测量方案比较简单,根据第二节的分析,测量速度仅取决于探头的扫描速度。通过测试前对系统动态范围的适当调整和测试后的Tie扫描校正以及位置误差补偿,在保证近场测量精度的同时,与单通道单频点近场测量相比测试效率提高了32倍。图7为某机载天线第二通道,11个频率的远场方向图叠加。图8为中心频率15 GHz时三个通道方向图比较。

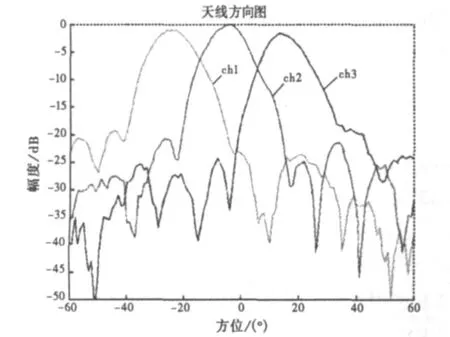
图8 中心频率三通道远场方向图比较

5.结 论

随着近场扫描架机械尺寸的增加,加工和控制精度的提高,近场测量的扫描速度也随之加快。探头的移动受到机械稳定性的限制,因此,对于大型天线的测试,总的扫描时间仍然需要几个小时。由于高速综合信号源和接收机的出现,使得扫描架能够以最快的速度运行,并在探头连续运动中实现多频点、多波束、多端口或者波束扫描的近场测量,明显地提高了测试效率。PNA系列网络分析仪以其快速的扫描能力、宽动态范围、低迹线噪声和灵活的连接能力,为现代天线和RCS测量提供了有力的技术保障。本文所讨论的系统配置和精度分析,在保证测量精度的同时,实现了多通道多波束扫频近场测量,有效地降低了测量时间。

[1] ALLEN C.NEWELLl.Current state-of-the-art in near-field antenna measurements[C]//IEEE Antennas&Propagation Society International Symposium,Boston,USA 2001.2001 Digest Volume 4:420-423.

[2] SWANSTROM J,PUII J,KWAN B,et al..Antenna and RCS measurement configurations using Agilent's new PNA network analyzers[C]//AMTA Proceedings,California,USA 2003.25th AMTA Annual Meeting&Symposium(AMTA 2003):573-579.

[3] SWANSTROM J.新型天线测试配置降低总测量测试时间[J].世界电子元器件,2005,(3):72-76.SWANSTROM J.Using pattern of antenna testing to reduce the testing time[J].Global Electronics China,2005,(3):72-76.(in Chinese)

[4] Agilent understanding and improving network analyzer dynamic range,Application Note 1363-1[DB/OL].Agilent Technologies Printed in USA 09/00 5980-2778EN.http://cp.literature.agilent.com/litweb/pdf/5980-2778EN.pdf

[5] FRANCIS M H,NEWELL A C,et al.Planar nearfield measurements of low-sidelobe antennas[J].Journal of Research of the National Institute of Standards and Technology,1994,99(2):14-167.

[6] HESS D W,MOREHEAD D R,MANNING S J.Speed and accuracy for near-field scanning measurements[DB/OL].http://www.mi-technologies.com/literature/mit8.pdf.

[7] 于 丁.平面近场辐射及散射测量关键问题研究[D].西安:西安电子科技大学,2004

[8] 张福顺.超低副瓣天线平面近场测量误差分析与补偿技术研究[D].西安:西安电子科技大学,1999.