雷电流测量用大型Rogowski线圈输出波形振荡现象分析

周璧华 朱凯鄂 李炎新 郭建明

(解放军理工大学工程兵工程学院,江苏南京210007)

1.引 言

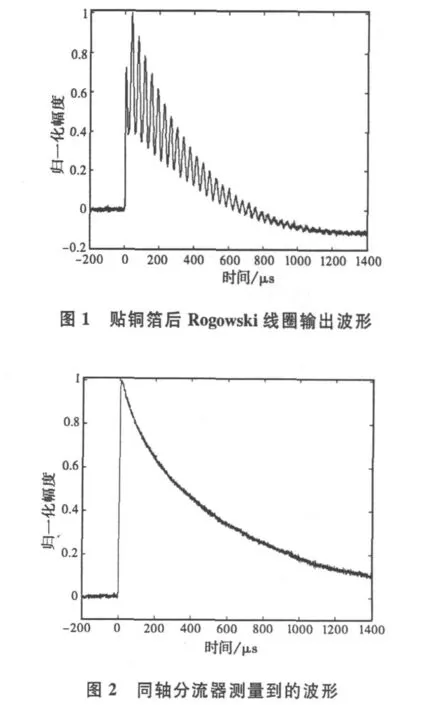
Rogowski线圈广泛应用于脉冲大电流的测量中[1-2,4],当选择Rogowski线圈测量柱状高塔自然雷电流时域波形时,其内径必须足够大,文献[3]通过增加线圈匝数获得高电感,实现了测量结果的自积分,去除了外加积分器带来的麻烦,同时可避免磁芯引入的非线性、磁饱和问题,从而为采用Rogowski线圈测量柱状高塔自然雷电流找到了一种较好的手段。本研究为防止外界杂散电磁场对其测量结果的干扰,在该线圈的外面贴了一层铜箔作为屏蔽层。可实验中发现,由于此屏蔽层的加入,使其输出的电流波形叠加了高频振荡,如图1所示,而同轴分流器测量到的波形如图2所示。

为此,对Rogowski线圈的频率响应及其影响因素进行了分析,考虑到铜箔与线圈之间的分布电容可能是引起附加振荡的主要因素,为此建立等效电路模型,对该分布电容导致Rogowski线圈输出波形出现振荡的现象进行了分析,得出的结论证实了这一判断,为下一步Rogowski线圈屏蔽设计的改进提供了依据。

2 自积分Rogowski线圈的测量原理

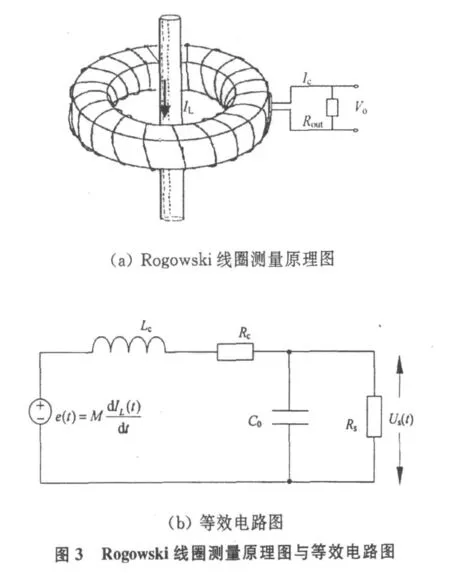
Rogowski线圈本质上是一种原边为单匝,副边为多匝线圈的电流互感器,如图3(a)所示,通过测量变化电流I L产生的磁场在副边线圈上的感应电压来确定原边线圈电流I L,图3(a)中I c为线圈上的感应电流。其等效电路图如图3(b)所示[2-7],图中Lc和R c分别为线圈的等效电感和电阻,C0为线圈的分布电容,R s为采样电阻。

由电磁感应定律可得线圈上产生的感应电动势为

式中,M为线圈与载流导体的互感系数。而由线圈的等效电路,在暂不考虑分布电容影响的情况下可得

此时线圈工作在自积分状态,无需外加积分电路。对角频率为 ω的分量须满足

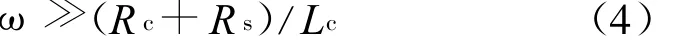
式(4)为自积分条件,并记 f l=(R c+R s)/(2πL c)为测量系统的下截止频率。由于雷电流低频成分丰富,为使线圈在测量雷电流时低频失真减至最小,应使 fl尽可能低。为此,应尽量增大线圈的电感Lc,减小线圈的损耗R c及采样电阻R s。

3 分布电容对Rogowski线圈动态特性的影响

线圈的分布电容会影响线圈的高频特性[5]。如果考虑分布电容的影响,由图3(b)可知,流过线圈的感应电流I c(t)为

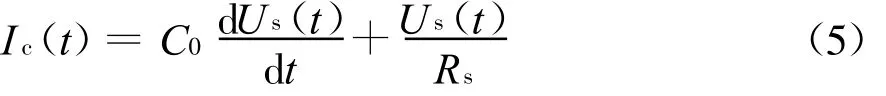
建立回路电压方程并化简得

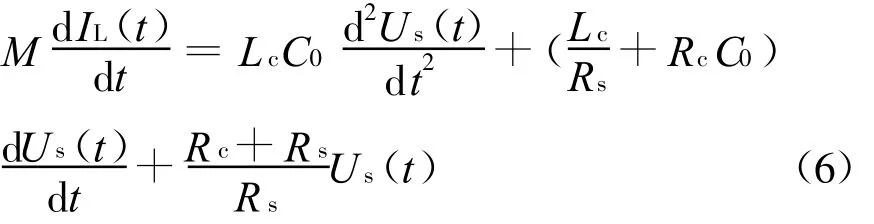
其传输函数为

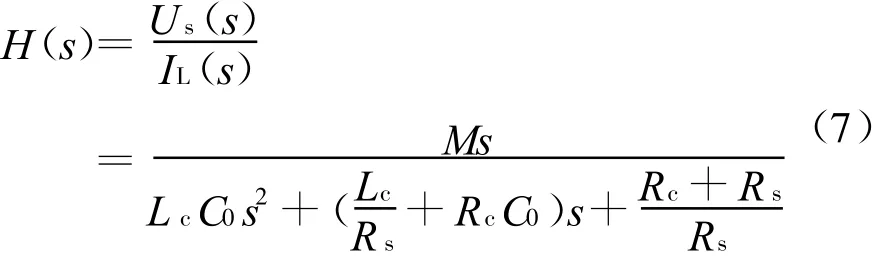
根据式(7)求得其下截止频率和上截止频率分别为

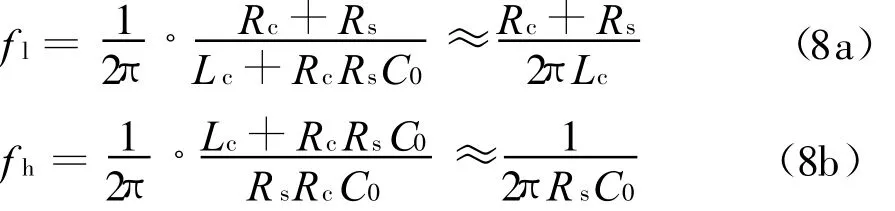
在计算线圈的谐振频率时,将其等效为图4所示电路。谐振时,有Im[Y(jω0)]=0,而

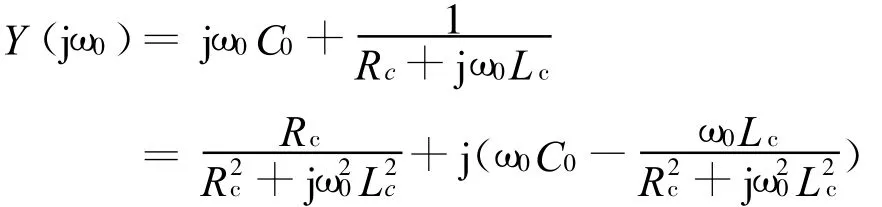
故有

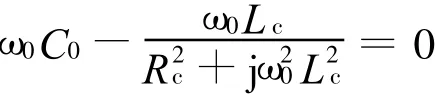
得谐振频率为

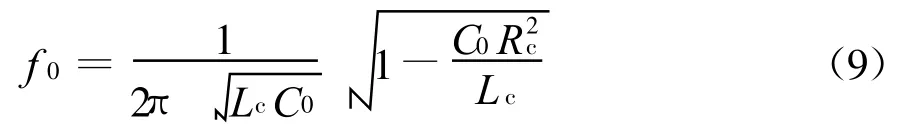
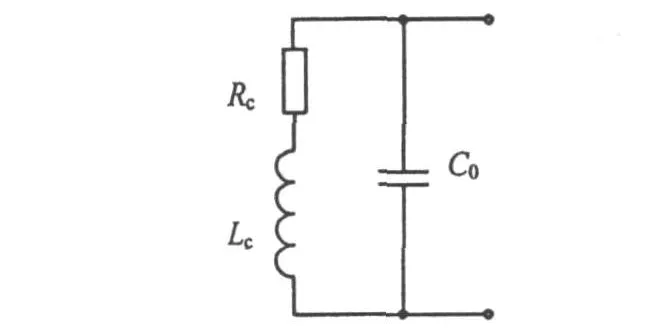
图4 线圈谐振时的等效电路图

3.1 分布电容的计算

为了防止外界杂散电场对线圈的耦合,需在线圈的外部加金属屏蔽层。此时Rogowski线圈的分布电容C0主要为外层的金属屏蔽层与绕制在柔性骨架上的线圈之间的电容。

图5所示Rogowski线圈截面为圆形,设其骨架截面半径为a,漆包铜线紧贴骨架缠绕;外屏蔽层横截面半径为b;线圈半径为r。因为r≫a、b,所以在计算分布电容C0时,可将其等效看作一个长度为2πr同轴型电容器,C0可按下式计算[8-9]

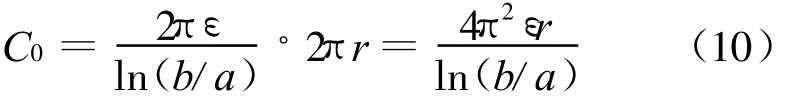
而实际线圈漆包铜线缠绕在圆形骨架上,在建模计算时将其近似为直的圆柱形导体,相当于增大了电容器两极板之间的正对面积,所以真实电容值比计算值要小得多。本实验中,线圈半径 r为0.25 m,骨架截面半径a为2.2 cm,屏蔽层横截面半径b为2.3 cm,计算出的电容值为1.9 nF。

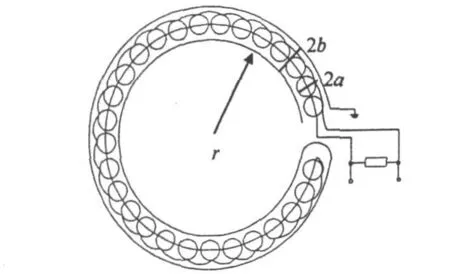
图5 Rogowski线圈结构示意图

4.实验分析研究

本实验所用的Rogowski线圈匝数为4000圈,计算出线圈的电感为

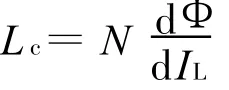
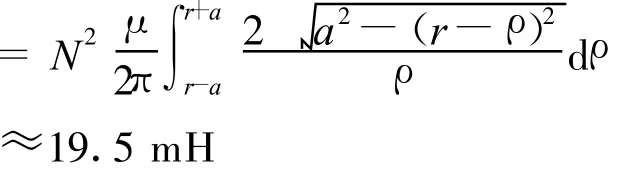
线圈实测的电感值约为23 mH,内阻R c为48 Ω,采样电阻Rs选用标称阻值为0.1Ω、功率为3 W的无感电阻[6]。

实验装置如图6所示,脉冲电流流过脉冲磁场模拟器的圆环,Rogowski线圈套在这个圆环上,所采集的电压信号由光发射机转变光信号经光纤传输至光接收机,再转变为电信号由示波器记录显示。在本实验中考虑了两种情况:一是线圈外加屏蔽层,即存在分布电容C0的情况;另外一种是不加屏蔽层,即去除C0这一影响因素。

图6 实验装置实物图

图7 是加屏蔽层和不加屏蔽层两种情况下Rogowski线圈的输出波形,从实验结果可以看出,加屏蔽层之后,由于分布电容C0的存在,线圈输出波形上叠加了高频振荡;而去掉屏蔽层后,振荡现象基本上消失。由式(9)计算出的振荡频率约为24 k Hz,而图7显示的振荡频率为70 k Hz,二者差距较大。这是因为计算分布电容时,将线圈视为为圆柱体,使电容C0的计算结果偏大,应加一个系数k加以修正,当k取为 0.2时,计算出的振荡频率为61 k Hz,与实验结果就比较接近了。

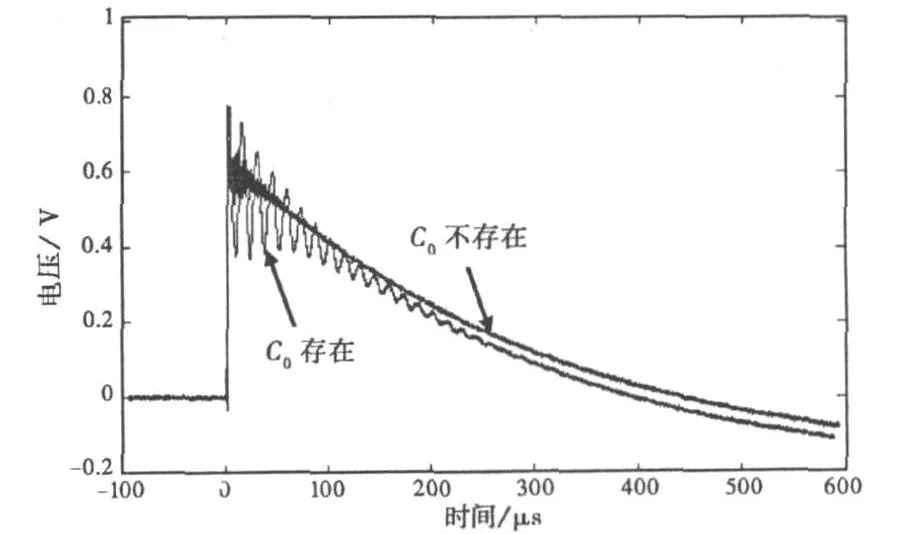
图7 分布电容对线圈测量结果的影响

为了进一步证明减小分布电容C0能够减小输出波形的振荡,在线匝外层套上热缩管和缠绕管后再贴上屏蔽层,使外部屏蔽层与内部线匝之间的距离增大,从而达到减小分布电容的目的。实验结果如下图8所示。由图8可见,当屏蔽层与内部线匝之间的距离很小时,输出波形前沿出现明显的振荡(图8中波形1);当屏蔽层与线匝间的距离增大后,输出波形前沿的振荡幅度明显减小(图8中波形2)。这不仅证实了测量波形前沿出现的振荡是由Rogowski线圈的分布电容引起的,而且为解决因线圈加屏蔽层出现振荡的问题找到了可行的办法。

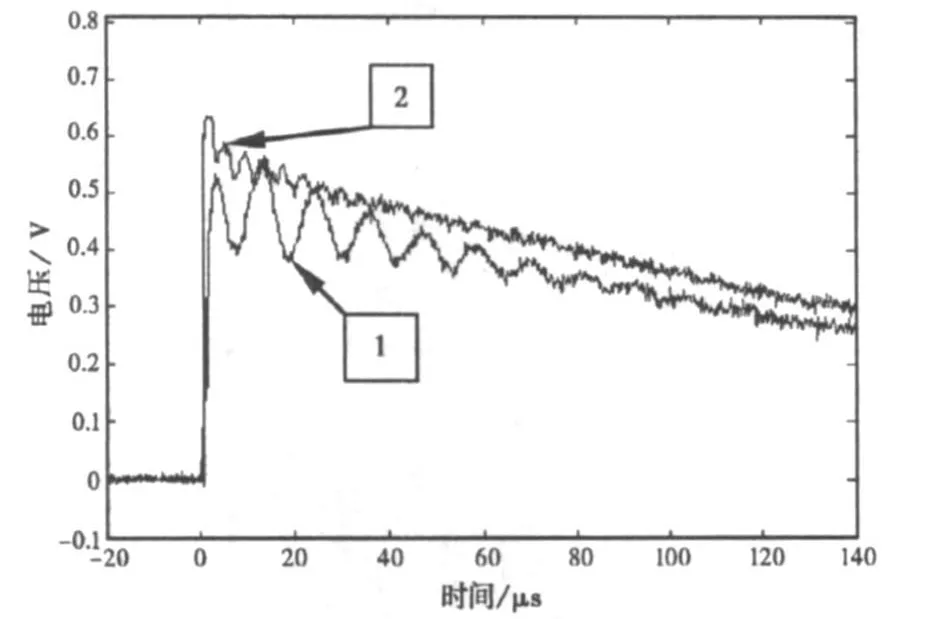
图8 增大屏蔽层与线匝之间的距离对测量结果的影响

5.结 论

本文针对Rogow ski线圈外加屏蔽层后输出波形出现的振荡现象,建模进行了分析,说明了屏蔽所用的铜箔与线圈之间的分布电容是引起附加振荡的主要因素。减小Rogowski线圈的分布电容,使附加振荡的频率提高至雷电流能量集中的频带以上,能有效减小线圈测量波形出现的附加振荡。在Rogowski线圈屏蔽设计中,增大外屏蔽层与线圈之间的距离,以减小线圈的分布电容,可减小甚至避免测试波形上的振荡现象。

[1] RAMBOZ JD.Machinable Rogowski coil,design,and calibration[J].IEEE Trans on Instrumentation and Measurement,1996,45(2):511-515.

[2] RAY W F,HEWSON C R.High performance Rogowski Current Transducers[C]//IEEE Industry Application Confer.Rome,Italy,2000,5:3083-3090.

[3] 杨 波,周璧华,石立华,等.雷电流测量专用柔性无磁芯大型Rogowski线圈[J].强激光与粒子束,2009,21(9):1421-1425.

YANG Bo,ZHOU Bihua,SHI Lihua,et al.Large Rogowski coil with flexible nonmagnetic core for lightning current measurement[J].High Power Laser and Particle Beams,2009,21(9):1421-1425.(in Chinese)

[4] 李维波.基于Rogowski线圈的大电流测量传感理论研究与实践[D].武汉:华中科技大学,2005.

LI Weibo.Study of sensor theory centered on Rogowski coil for heavy current measurement application[D].Wuhan:Huazhong University of Science and Technology,2005.(in Chinese)

[5] 李维波,毛承雄,陆继明,等.分布电容对Rogowski线圈动态的影响研究[J].电工技术学报,2004,19(6):70-73.

LI Weibo,M AO Chengxiong,LU Jiming,et al.Study of influence of the distributed capacitance on dynamic property of Rogowski coil[J].Transactions of China Electrotechnical Society,2004,19(6):70-73.(in Chinese)

[6] 梁 瑜,蒋兴良,杨 庆,等.雷电流测量用Rogowski线圈频谱特性分析[J].高电压技术,2005,31(5):18-20.

LIANG Yu,JIANG Xingliang,YANG Qing,et al.A-nalysis on the spectrum of Rogowski coil applied to measuring lightning current[J].High Voltage Engineering,2005,31(5):18-20.(in Chinese)

[7] 方 志,赵中原,邱毓昌,等.Rogowski线圈的高频特性分析[J].高电压技术,2002,28(8):17-18.

FANG Zhi,ZHAO Zhongyuan,QIU Yuchang,et al.Analysis on the High-frequency characteristics of Rogowski coil[J].High Voltage Engineering,2002,28(8):17-18.(in Chinese)

[8] ROBLESG,ARGIIESO M,SANZI J,et al.Identification of parameters in a Rogowski coil used for the measurement of partial discharges[C]//IEEE Instrumentation and Measurement Technology Conference.Warsaw,Poland,May 1-3,2007.

[9] GURU B S,HIZIROGLU H R.Electromagnetic Field Theory Fundamentals[M].2nd ed.Beijing:China Machine Press,2005.