两阶段卡尔曼滤波自适应交互式多模型算法

廖 阳,王 睿,曾昭博,2,熊加遥

(1.空军工程大学导弹学院,陕西三原 713800;2.93617部队,北京 101400)

0 引言

机动目标跟踪理论是一个比较前沿的理论,在军事领域和民用领域都有着广泛的应用。民用方面如:海上导航、空中交通管制等;军事应用如:导弹防御、战场监视、精确制导等。其中,机动目标跟踪在军事上的应用显得尤为重要。

针对机动目标的跟踪问题,很多学者进行了相关的研究,并提出了各种不同的方法。其中一种比较典型的方法是交互式多模型方法[1],利用多个子滤波器的加权和构成系统的最终输出。对于一个机动目标而言,有可能采取各种不同的机动,因而不可能采用较少的子滤波器来准确描述目标的机动。为此,需要用到大量具有不同参数的子滤波器,但是研究表明使用过多的子滤波器并不一定能解决问题,反而可能陷入两难的境地:一方面,使用过多的子滤波器会使计算量大幅度增加;另一方面,来自子滤波器之间不必要的竞争,反而使得性能下降。

为了在减少子滤波器数量的同时,有效提高跟踪精度,降低计算量,本文设计了一种自适应交互式多模型机动目标跟踪算法。

1 机动目标跟踪的IMM算法与两阶段卡尔曼滤波

1.1 目标机动模型

在二维平面内,目标的机动模型可以表示为如下形式[2]:

式中,X(k)为状态向量;Φ为已知状态转移矩阵;Γ为系统输入矩阵;W(k)为系统噪声;U(k)为未知系统确定加速度。

测量方程为:

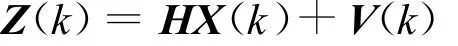
式中,H为系统测量矩阵;V(k)为测量噪声。假定W(k),V(k)分别为均值为零,方差为Q,R的白噪声。

1.2 IMM算法

IMM估计的实质是对多个单独模型跟踪的估计值加权求和,得到组合状态估计,其中模型有效的概率在状态和误差协方差组合中起加权作用,用马尔可夫链实现不同模型的转换[3]。在每一个滤波周期内包括4步:输入交互、子模型条件滤波、子模型概率更新、组合估计。其具体算法如下[4]:

2)模型条件滤波

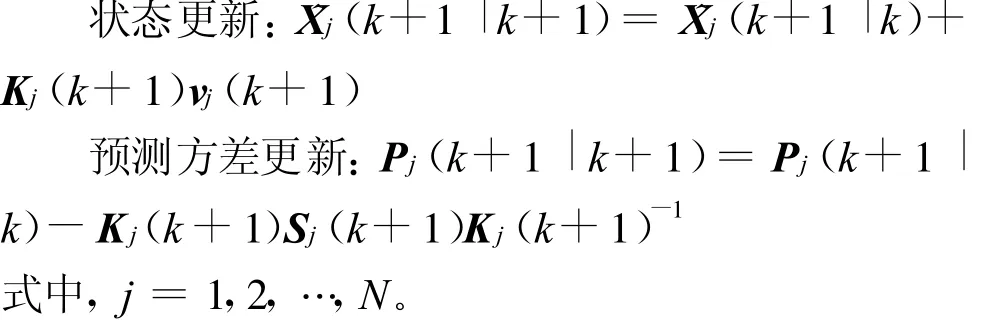
3)模型概率更新

模型概率:

式中,j=1,2,…,N。

4)组合估计

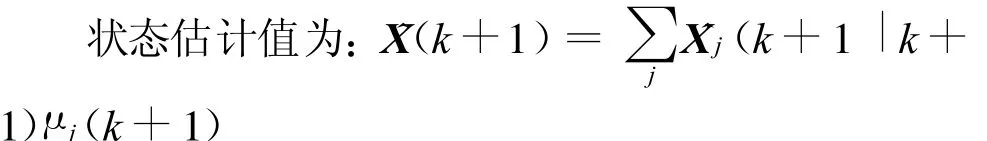
协方差矩阵为:

1.3 两阶段卡尔曼滤波

两阶段卡尔曼滤波器[5]由两个部分构成:一个无偏滤波器与一个有偏滤波器。无偏滤波器为一个具有噪声方差Qf的标准卡尔曼滤波器。有偏滤波器的方程为[6]:

2 两阶段自适应交互式多模型算法

IMM估计算法的精度由具有一种机动模型的子滤波器确定;而采用过多的子滤波器不但会引起各个子滤波器之间的竞争,而且也会使得系统的计算量大大增加[6]。如表1所示。

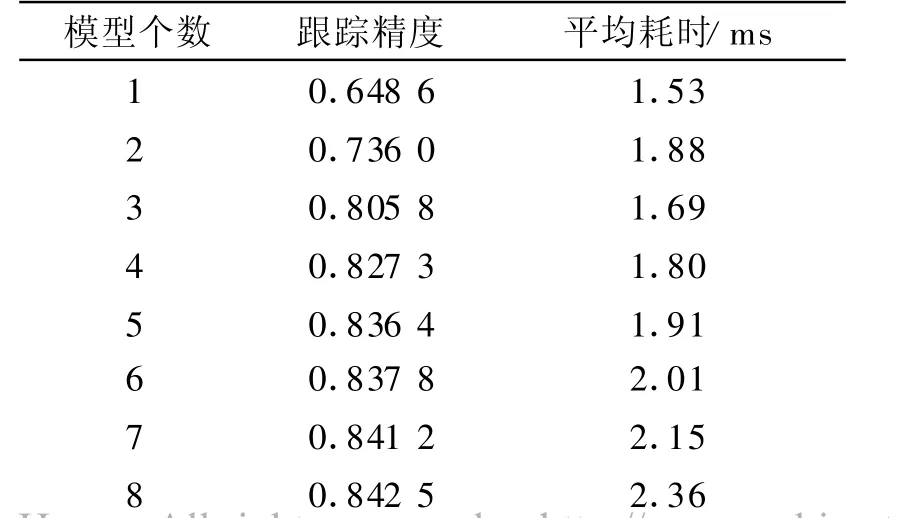
表1 模型个数对跟踪结果影响Tab.1 The infection of model amounts to track result

假设使用IMM估计算法跟踪一个匀速机动目标,随着模型个数增多,跟踪精度增加,但计算量也相应增加,导致跟踪周期平均耗时增加。

为此,本文在此基础上引入两阶段卡尔曼滤波器,首先由两阶段卡尔曼滤波器给出加速度的估计值,然后,以此加速度的估计值为基础,建立少量的子滤波器进行IMM滤波,从而在保证具有一定跟踪精度的同时,有效减少子滤波器的数量,降低计算量。在建立子滤波器时,可以首先根据估计值选择一个子滤波器的加速度,而其他几个子滤波器的加速度分布在其周围。例如,如果具有5个子滤波器则选择加速度为:ae,ae(1±ε1),ae(1±ε2)(ε1与ε2小于1),ε1与ε2选择过大或过小会出现误跟或失跟现象。所以在实际实施过程中,参数ε1与ε2需要根据实际情况合理选取。

基于此思想,具体的自适应IMM滤波的工作流程如图1所示(通常,参数ε1与ε2需要根据实际情况合理选取)。

图1 自适应IMM滤波算法流程Fig.1 The flow chart of adaptive IMM filter algorithm

3 仿真实验

假设目标初始状态值[30 km,-172 m/s,30 km,-246 m/s]T,目标在1～29 s,90～119 s,180～200 s作直线运动;30～89 s向右转弯,转弯率2.9(°)/s;120～ 179 s向左转弯 ,转弯率 -2.0(°)/s,目标运动轨迹如图2所示。

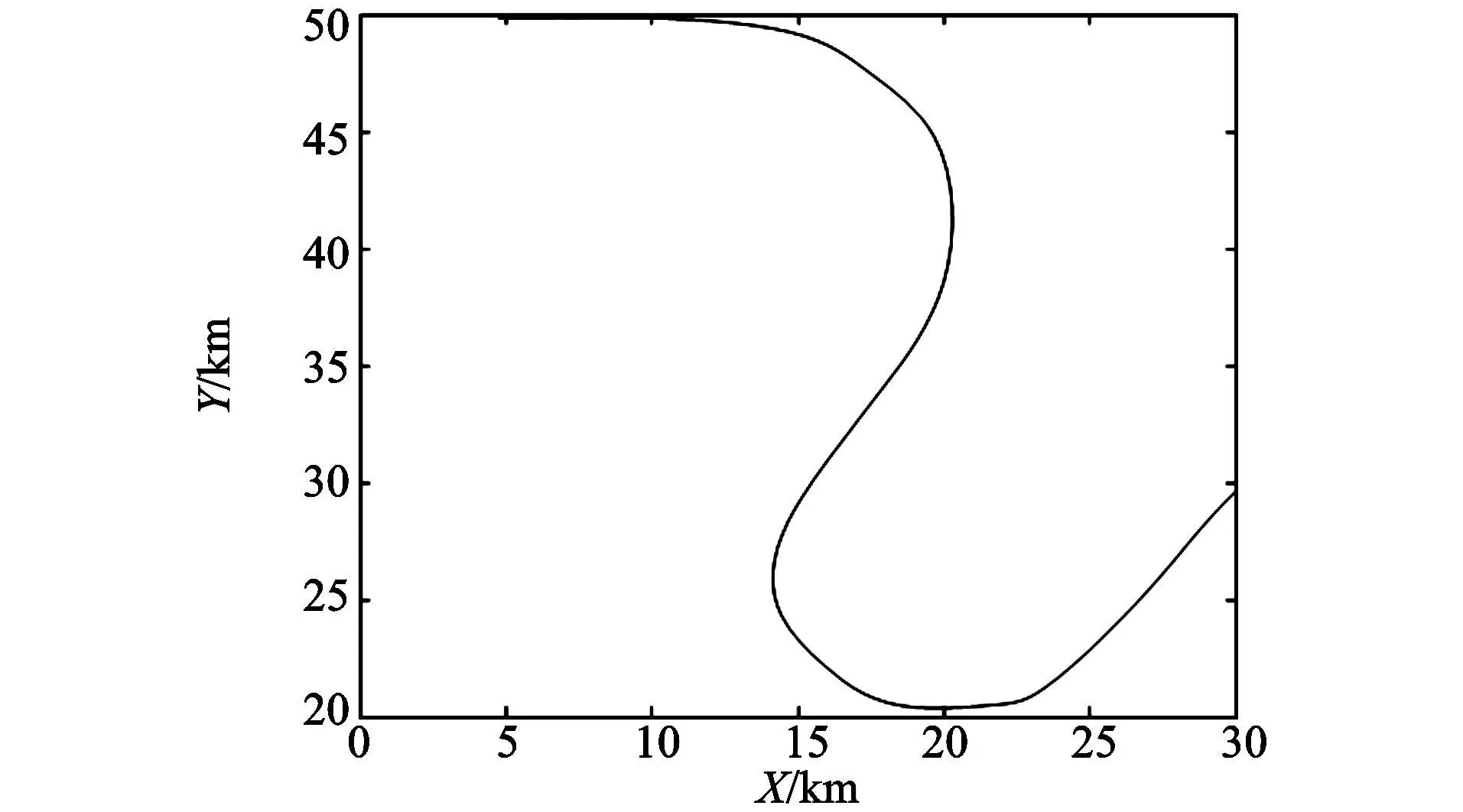
图2 目标运动轨迹Fig.2 Track of target

为了验证本文所提出方法的有效性,将本文方法与文献[7]中的半适应IMM 方法(half adaptive IMM,HAIMM)进行对比。在仿真时,取HAIMM的子滤波器数量为3个,其加速度选择为:at=0±5,初始模型概率为[1/3,1/3,1/3],Markov转移概率矩阵为:

当采用本文方法时,选择子滤波器加速度分别为ae,ae±1.5,其他条件同上。其中ae为两阶段卡尔曼滤波的估计值。

两种算法仿真对比如图3与图4所示。其中,图3为位置跟踪误差,(a)、(b)分别是相应X轴与Y轴跟踪误差对比曲线;图4为速度跟踪误差,(a)、(b)分别是相应X轴与Y轴跟踪误差的对比曲线。

从图3与图4中两种方法的仿真对比可看出:本算法在目标机动时刻的位置和速度误差相比文献[7]中的HAIMM算法明显要小,跟踪效果得到了明显改善,从而也验证了本文算法的有效性。

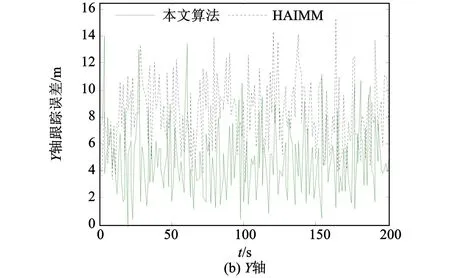
图3 位置跟踪误差Fig.3 The position RMSE of target

图4 速度跟踪误差Fig.4 The velocity RMSE of target

4 结论

本文采用一般的交互式多模型算法中子滤波器的选择问题,结合两阶段卡尔曼滤波器和交互式多模型算法设计了一种自适应的交互式多模型算法,有效地减少了子滤波器的数量,同时在一定程度上也提高了跟踪的精度。

[1]Bar-Shalom Y,Blair W D.Multitarget-multisensor tracking:applications and advances[M].Boston:Artech House,2000.

[2]Li X R.Multiple-model estimation with variable structure-partⅡ:model-set adaptation[J].IEEE Transactions on Automatic Control,2000,45(11):2 047-2 060.

[3]Daeipour E,Bar-Shalom Y.An interacting model approach for target with Glient noise[J].IEEE Transactions on Aerospace and Electronics,1995,31(2):706-716.

[4]L A Johnston,V Krishnamurthy.An improvement to the interacting multiple model(IM M)algorithm[J].IEEE Transactions on Signal Processing,2001,49(12):2 909-2 923.

[5]Alouani A T,Xia P,Rice T R,et al.A two-stage Kalman estimator for state estimation in the presence of random bias and for tracking maneuvering targets[C]//Proceedings of 30th IEEE Conference on Decision and control.New York:IEEE,1991:2 059-2 062.

[6]Alouani A T,Xia P,Rice T R,Blar W D On the Optimality of Two-Stage State Estimation in the presence of Random Bias[C]//IEEE Trans on Automat.Contr.US:IEEE,1993 AC:1 279-1 282

[7]Lin H J,D P Athertion.Invetigation of IMM tracking algorithm for maneuvering target tracking[C]//First IEEE Regional Conference on Aeropace Control System.US:IEEE,1993:113-117.