柔性机构动态可靠性分析的模糊响应面方法

于霖冲

(1.北京航空航天大学,北京 100091;2.厦门理工学院,福建 厦门 361024)

0 引言

机构中如果包含了一个或者多个易产生较大变形的细长构件,这种细长构件在运动过程中会产生变形与运动的耦合,动态参数会出现“波动”,通常将这种机构叫做柔性机构。柔性机构运动副之间的摩擦和碰撞在柔性机构运动过程中存在很大的不确定性。如果动态参数“波动”在安全临界值附近,将使柔性机构系统可靠性的判定更加复杂,增加了机构系统的模糊性。随着轻质、高速的机械系统不断出现,构件在速度和柔度上不断加大,构件的柔性变形也加大。在高精度和高可靠性的要求下,构件变形已不能忽略[1]。因此,模糊随机柔性机构系统的动态性能可靠性研究具有十分重要的现实意义。

美国学者Zateh在20世纪70年代提出了模糊理论[2],在结构静态模糊可靠性分析方面取得了许多成就[3-8]。其中,白广忱教授和王光远院士对以可靠度为目标函数的大系统多目标优化问题提出了模糊分配方法[3];Verma和Knezevic提出了概念设计阶段机构系统可靠度的模糊分配方法[4];Li Bing等[5]、董玉革等[6]、白广忱和黄洪钟等[7-9]的工作使模糊可靠性研究得到更加广泛的应用,但在机构动态可靠性应用上还有待进一步深入探索。本文在上述研究成果的基础上,提出了一种柔性机构动态性能可靠性分析的新方法。

1 模糊响应面方法的基本理论

响应面法(Response Surface Method,简称RSM)是由Bucher在20世纪90年代提出的,是在未知功能函数时进行可靠性分析的一种近似方法,在结构静态可靠性分析上取得了很好的效果[10]。

设xi(i=1,2,…,n)为可靠性分析中的n个任意分布的独立随机变量,由这些随机变量表示的极限状态方程为:

响应面方法的基本思想就是重构一个近似的极限状态方程g′(x)来近似替代g(x):

常规重构响应面g′(x)的方法是利用不含交叉项的二次多项式表示响应面函数,待定系数为2n+1个:

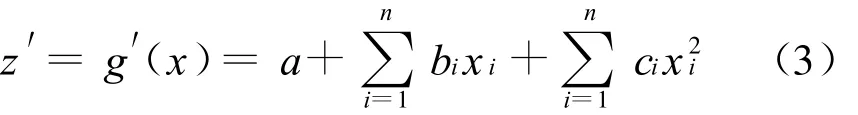
式(3)可以通过系列确定性的实验确定,解线性方程组得到2n+1个待定系数,从而确定由二次多项式表示的响应面函数。得到响应面函数后,可以用一次二阶矩方法求出可靠度指标和设计验算点。通常情况下,初始迭代点一般取均值点,如不满足可靠度指标的精度要求,经线性插值得新的展开点,直到精度满足要求。具体求解计算步骤见文献[10]。

2 动态可靠性分析的模糊响应面方法

传统的RSM方法并没有考虑模糊性,也没有考虑安全失效状态随时间的动态变化。单纯考虑随机变量的传统RSM方法失效状态表达为:

如果考虑状态的模糊性,将安全状态和失效状态分别作为状态空间的模糊集合:模糊安全域D s和模糊失效域Df,对应的极限状态函数为:

如果考虑安全失效状态的模糊性,将安全状态和失效状态分别作为状态空间的模糊安全域D s和模糊失效域D,考虑安全和失效状态随时间的动态变化,这时极限状态函数为时变的模糊极限状态函数(t):

特别地:当取 μf=0,μs=1 时,或者取 μf=1,μs=0时分别表示不考虑状态模糊的情况。

在确定μf或 μs后,假设各个状态Y(tj)之间相互独立,可以求得失效概率为:

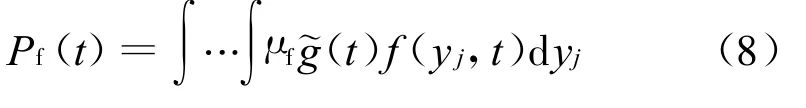
同理,动态可靠度为:

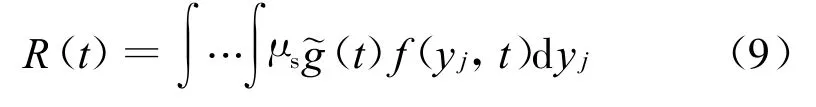
式(9)中,t∈T,f(yj,t)为Y(t)的联合概率密度函数。这里,显然有:

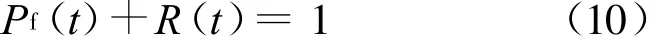
考虑状态模糊性,通过系列确定性的实验将极限状态函数转化为区间函数[11-15]:

这样,就将一个模糊响应面由两个确定的响应面表达,通过一次二阶矩方法分别求出对应的验算点和可靠度指标βL和βU,则:

根据模糊数学的分解定理,利用λ水平截集方法,可以求出可靠度指标β:

3 柔性机构模糊动态可靠性计算实例

将柔性机构系统作为一个动态模糊随机系统,其模糊性体现在机构的模糊随机动态响应和动态参数的模糊失效状态上面,通过多柔体系统动力学分析,求出模糊随机变量的动态响应,利用响应面重构极限状态方程。

3.1 柔性机构模型

图1为空间站柔性展开机构平面模型[3-5]。机构系统由B0—B15共16个构件组成。通过B8和B11两台电机驱动螺旋副B7和B12,使得B0和B3之间的距离以及B3和B6之间的距离缩短,完成机构的展开运动,图1所示为机构完全展开的状态。机构系统中的大尺寸轻质构件 B 、B 、B 、B 、B 、B 和B15在展开过程中会产生较大的变形,将它们作为等截面均质柔性梁,展开机构中的其它构件视为刚体,展开机构为一个包含7个柔性构件的柔性机构。

图1 展开机构Fig.1 Expand mechanism

根据多柔体系统动力学原理,利用Lagrange乘子法建立广义的柔性机构动力学方程为[1]:

根据式(14)进行仿真,以柔性构件B2的角加速度为研究对象,确定性仿真结果如图2所示,机构动态响应由于耦合的原因非线性程度较高。

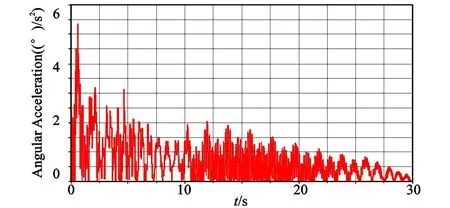
图2 动态响应Fig.2 Dynamical response

确定柔性机构系统的随机变量为:驱动力矩M d、摩擦力矩M f(单位n◦mm)、驱动时间t(单位s)、阻尼系数f以及装配误差(为便于计算,以坐标x p和yp表示,单位mm)。表1为随机变量设计值和方差、100组抽样数据的均值和方差。

3.2 柔性机构模糊响应面分析

给定模糊集合Ds的隶属度μs,本文采用最常用的正态分布隶属度函数,设X(t)为机构在t时刻的动态响应,则μ为:

式中,a(t)为模糊参数,根据专家经验确定;b(t)为t时刻模糊分布的标准差。

根据表1数据进行最大角加速度的动态仿真,确定构件B2的最大角加速度的设计规定值为aθ2≤4.7 rad/s2。再根据式(11),在上述分析的基础上可以计算由两个确定的响应面表达的模糊响应面。确定模糊分布参数b(t)为0.01,通过一次二阶矩方法分别求出对应的可靠度指标βL和βU分别为4.689 8和4.710 8,迭代次数为5次。由式(13)计算得到一定模糊水平截集下的可靠度,计算结果为0.936 2。

4 结论

考虑状态模糊的情况确定柔性机构的动态可靠度更加符合工程实际,模糊响应面方法为可靠性分析提供了一种新方法。

通过柔性机构实例仿真分析,证明该方法具有迭代次数少,计算速度快,精度高的优点,适合于复杂系统的仿真,尤其在随机变量数量较多的情况下,可以极大缩减计算时间,节约计算成本。

该方法具有很强的拓展性,可以按照本文方法求解其他运动参数的可靠度。

[1]Shabana A A.Flexible Multibody Dynamics:Review of Past and Recent Developments[J].Multibody System Dynamics,1997(1):189-222.

[2]Zateh L A.Theconcept of a linguistic variableand its application to approximate reasoning-I[J].Information Science,1975(8):199-249.

[3]白广忱,王光远.系统可靠度的模糊优化分配[J].哈尔滨BAI Guangchen,WANG Guangyuan.Fuzzy optimal allocation of system reliability[J].Journal of Harbin Architecture&Civil Engineering Institute,1994,27(6):1-6.

[4]Verma D,Knezevic J.A fuzzy weighted wedgemechanism for feasibility assessment of system reliability during conceptual design[J].Fuzzy Sets And Systems,1996,83:179-187.

[5]LI Bing,HU Meilin,XU Kai.A practical engineering method for fuzzy reliability analysis of mechanical structures[J].Reliability Engineering and System Safety,2000,67:311-315.

[6]董玉革,陈心昭,赵显德,等.模糊可靠性理论在机构运动可靠性分析中的应用[J].应用科学学报,2002,20(3):316-320.DONG Yuge,CHEN Xinzhao,ZHAO Xiande,et al.An application of fuzzy reliability theory in the reliability analysis of mechanism movement[J].Journal of Applied Science,2002,20(3):316-320.

[7]白广忱,黄洪钟.机械系统可靠性的多目标模糊优化设计[J].机械设计,1998(1):12-13.BAI Guangchen,HUANG Hongzhong.Multi-objective fuzzy optimization design for the reliability of mechanical systems[J].Mechanical Design,1998(1):12-13.

[8]黄洪钟,白广忱.串联系统可靠性分配的模糊优化方法[J].机械设计与制造,1996(5):10-12.HUANG Hongzhong,BAI Guangchen.Fuzzy optimization of series system reliability apportionment[J].Mechanical Design&Manufacture,1996(5):10-12.

[9]白广忱,张建国.基于模糊状态判据的应力──强度干涉理论[J].机械设计与制造,1998(5):1-2.BAI Guangchen,ZHANG Jianguo.The stress strength interference theory based on fuzzy state criterions[J].Machinery Design&Manufacture,1998(5):1-2.

[10]Bucher C G,Bourgund U.A fast and efficient response surface approach for structural reliability problems[J].Structural Safety.1990,7:57-66.

[11]吕震宙,岳珠峰,张文博.弹性连杆机构广义刚度可靠性分析的数值模拟法[J].计算力学学报,2004,21(1):62-66.LÜZhenzhou,YUE Zhufeng,ZHANG Wenbo.Numerical simulation method for random-fuzzy reliability analysis of elastic linkage mechanism stiffness[J].Chinese Journal of Computational Mechanics,2004,21(1):62-66.

[12]Akpan U O,Koko T S,Orisamolu I R.Respond surface based fuzzy analysis of structural systems[R].US:AIAA,A00-24744,2000:1 640.

[13]刘长虹,陈虬,吕震宙,等.工程模糊随机结构失效模式的确定方法[J].机械强度,2001,23(3):302-304.LIU Changhong,CHEN Qiu,LÜZhenzhou,et al.Determination for the failure models in the fuzzy-random engineering structures[J].Journal of Mechanical Strength,2001,23(3):302-304.

[14]Paola M D.A method for the probabilistic analysis of nonlinear systems[J].Probabilistic Engineering Mechanics,1995(10):1-10.

[15]吕震宙,岳珠峰.模糊随机可靠性分析的统一模型[J].力学学报,2004,36(5):533-539.LÜZhenzhou,YUE Zhufeng.Unified reliability model for fuzziness and randomness of the basic variables and state variables in structure[J].ACTA MECHANICA SINICA,2004,36(5):533-539.