线性调频连续波时频分析中的余弦变换方法

赵继广,宋一铄,张智诠

(1.装甲兵工程学院控制工程系,北京 100072;2.装备指挥技术学院,北京 101416)

0 引言

线性调频连续波(Linear Frequency Modulation/Continuous Wave,LFM/CW)体制测距系统,通过对回波信号与本振信号混频后得到的差频信号频率的测量实现对目标距离的测量[1]。该测距系统在一些距离范围内获得的差频信号的初始相位近似为0,目前一般利用傅里叶变换进行时频分析[2]从而得到差频信号的频率,但由于其测距分辨力不够高且运算量大,因此难于实现实时多距离分辨。为此,本文提出利用余弦变换进行时频分析的方法。

1 傅里叶变换与余弦变换

傅里叶变换是进行频谱分析的重要方法,余弦变换是傅里叶变换的一部分。傅里叶变换具有普适性,对于一般信号都能给出正确的频谱。具体到一些拥有特殊性质的信号,可以考虑利用其他时频分析方法处理,从而突出某一方面的性能。例如对于初始相位为0(或近似为0)的余弦信号,余弦变换不仅能够给出近似正确的频谱,还具有较小的运算量[3]和更高的频率分辨力。

1.1 傅里叶变换

在实际应用中受器件和环境等因素的影响,所得到的差频信号的信噪比较低。由于傅里叶变换对噪声抑制能力强,所以一般用其获得信号频谱信息。根据傅里叶变换的定义,连续非周期信号s(t)的傅里叶变换可以表示为[4]:

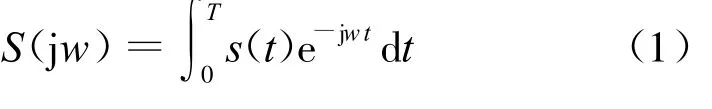
将式(1)展开,得到

对上式取模,即得到信号的频谱。由(2)式可知:将信号s(t)分别与各种频率下的余弦和正弦信号进行混频,再将每一个频率下的两个混频结果取模就得到了该频率下的频谱幅值。由于连续非周期信号等同于周期无限大的周期信号,所以得到的频谱应该被理解为频谱密度。信号s(t)中包含的任一频率分量的初始相位都是未知的,频谱分析不应受到未知初始相位的影响,所以傅里叶变换采用正交混频并取模的方式,使得只要信号s(t)中存在该频率分量,计算结果就会在该频率点上得到峰值且不会受到其初始相位的影响。

对频率为 fIF,时长为 T的余弦信号,无论其初始相位如何,对其进行傅里叶变换后,其频域将呈现一个峰值在 f IF处的SINC函数,如图1所示。

图1 1 ms时长矩形窗函数的傅立叶变换频谱图Fig.1 The frequency spectrum of 1 ms-lasting rectangular window in Fourier transform

1.2 余弦变换

连续非周期信号S IF的余弦变换为[5]:

在余弦变换下,由于没有涉及正交混频,所以信号的初始相位不同会引起频谱误差,即通过余弦变换得到的频谱会因为信号的初始相位而出现频谱偏移和畸变。例如对一时长为T、频率为 f 1且初始相位φ0不为0的余弦信号

作余弦变换,得到信号频谱

由式(7)可知用余弦变换得到的频谱函数在差频信号频率点上的幅度会受到初始相位的影响。只有当信号初始相位为0(或近似为0)时,才能得到和傅里叶变换一致(或近似一致)的结果,即在频域呈现一个峰值在 f IF处的SINC函数,如图2所示。

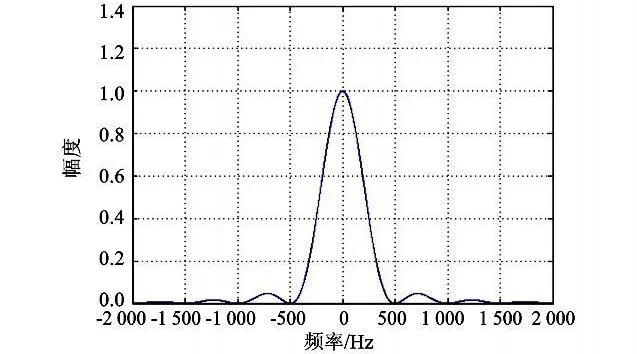
图2 1 ms时长矩形窗函数的余弦变换频谱图Fig.2 The frequency spectrum of 1 ms-lasting rectangular window in cosine transform

2 线性调频连续波时频分析的余弦变换原理

LFM/CW体制测距系统将回波信号与本振信号混频得到差频信号,该差频信号的频率与目标距离间存在线性关系[1]。在实际应用中,综合考虑信号信噪比和抗干扰能力等因素,一般利用傅里叶变换提取差频信号的频率。如果在一次测量中存在两个或以上不同距离的目标,那么得到的差频信号中也含有与这些目标距离对应的频率。分辨开这些频率就分辨开了这些不同的距离。由第一节中傅里叶变换和余弦变换的性质可知,对于时长为 T的余弦信号,两种变换下的频率分辨力分别为 T-1和0.5T-1,但使用余弦变换时要求信号的初始相位近似为零以避免频谱偏移和失真。LFM/CW体制测距系统得到的差频信号由一个或多个余弦信号组成,通过改变系统参数,这些余弦信号的初始相位在一些距离范围内近似为0,此时利用余弦变换可得到近似正确的信号频谱。这使余弦变换在 LFM/CW测距中的应用成为可能,即可利用余弦变换处理差频信号,使得在差频信号时长不变的情况下,将频率分辨力提高到使用傅里叶变换时的两倍。

3 余弦变换在LFM/CW体制测距系统中的应用

3.1 余弦变换下LFM/CW体制测距系统的测距分辨力

具体到 LFM/CW 体制测距系统[6],由于一个周期内观察到的差频信号的频率为fIF,时长约等于扫频周期T,故对其进行傅里叶变换后,其频域将呈现一个峰值在 fIF处的SINC函数,此时SINC函数的主瓣宽度为 T-1,频率分辨力为T-1,即如果两个差频信号相差小于T-1则会造成频谱叠加而无法分辨。所以如果发射信号扫频带宽为B,则利用傅里叶变换处理被矩形窗截短的差频信号时,LFM/CW体制测距系统的测距分辨力为:

这说明如果系统探测到的两个目标之间的距离差小于0.5cB-1,则不能正确分辨两个目标。相比在傅里叶变换下得到的结果,利用余弦变换得到的SINC函数主瓣宽度不再是T-1,而是0.5T-1。即对于初始相位为0(或近似为0)的余弦信号,在信号时长为T的情况下,其频率分辨力为0.5T-1,比傅里叶变换提高了一倍,相应的测距分辨力也提高到

3.2 差频信号分析

LFM/CW体制测距系统得到的差频信号由回波信号与本振信号经混频滤波后得到,在τ≤t≤T时间内,其形式由式(10)给出[6]。

式中,τ为回波时延,f 0为信号扫频起始频率,k为扫频斜率。由式(10)可知,当系统参数和目标距离R一定时,差频信号是一个频率和初始相位都确定的余弦信号,其频率为kτ,初始相位为2πf 0τ。由于

则初始相位为

分析式(12)可知,当

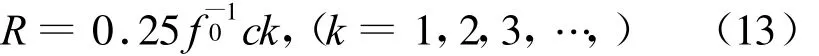
差频信号的初始相位为kπ,对于傅里叶变换和余弦变换而言,相当于一系列初始相位为0的余弦信号,当

差频信号的初始相位为kπ-0.5π,相当于一系列初始相位为0.5π的余弦信号。

4 傅里叶变换与余弦变换下LFM/CW体制测距系统距离分辨仿真

4.1 余弦变换下系统参数的设定

由前面的分析可知,傅里叶变换采用正交混频并取模的方式避免了信号初始相位对频谱分析的影响,而当信号初始相位为0(或近似为0)时,使用余弦变换的方法同样可以得到近似正确的频谱。具体到LFM/CW体制测距系统中得到的差频信号,由前面的分析可知,若目标距离

则此时初始相位φ0将趋近于0,此时该距离范围内目标对应的一系列差频信号的初始相位可以近似看作为0,这使得利用余弦变换处理差频信号成为可能。若差频信号频率f IF和初始相位φ0满足下面的条件

则目标距离R的范围可由式(17)得到

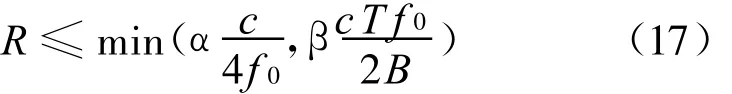
限制参数α、β可以根据具体要求的频谱误差和滤波器性能设定。根据这些限制参数,令

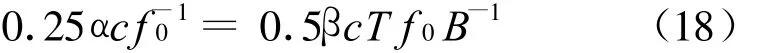
便得到利用余弦变换可测量最大目标距离

例如,若令α=0.05,β=0.7则保证了由目标距离引入的初始相位最大不超过0.05π以及差频信号为扫频起始频率 f 0的0.7倍,当扫频带宽B=100 MHz,扫频周期T=10 ms时,得到可测量最大目标距离约为198 m。

4.2 测距分辨力仿真

为了验证利用余弦变换提高LFM/CW体制测距系统测距分辨力的可行性,现对20 m处的多目标进行距离分辨,要求测距分辨力为0.25 m,扫频周期T=1 ms。根据分辨力要求及参数限制,扫频起始频率应为f 0=100 k Hz,扫频带宽B=300 MHz。现假设三个目标分别距离系统为19.75 m,20 m,20.25 m利用余弦变换得到的仿真结果如图3所示。

图3 利用余弦变换进行20 m附近三目标距离谱仿真Fig.3 The distance spectrum simulation of the 3 targets around 20 m using cosine transform

从图中可以看出,在式(15)的条件下差频信号的初始相位对测距造成的影响很小,余弦变换不仅给出了准确的距离信息而且分辨出了相距0.25 m的三个距离。此时若使用傅里叶变换,则根据式(8)得到其测距分辨力为0.5 m,不能对三个距离进行分辨,如图4所示。

现将LFM/CW体制下利用余弦变换进行距离分辨的方法总结如下:

1)根据测距分辨力要求确定扫频带宽B;

2)根据目标距离及限制参数,由式(17)确定起始扫频频率f0和扫频周期T,由式(19)确定最大距离Rmax;

3)对差频信号进行余弦变换,完成分辨。

图4 利用傅里叶变换进行20 m附近三目标距离谱仿真Fig.4 The distance spectrum simulation of the 3 targets around 20 m using Fourier transform

5 结论

本文提出了调频连续波时频分析中的余弦变换方法,该方法利用余弦变换在处理零初始相位单频信号时具有高频率分辨力这一优点,将其应用于处理LFM/CW体制测距系统得到的差频信号从而提高测距分辨力。理论分析和仿真证实了在一定距离范围内,使用余弦变换处理差频信号可以得到近似正确的频谱,相比使用傅里叶变换时其测距分辨力提高了一倍。

[1]丁鹭飞,耿富录.雷达原理[M].西安:西安电子科技大学出版社,2006:177-182.

[2]高庆地,李世光,高正中,等.傅里叶变换的数学再认识[J].数据采集与处理,2008,23(增刊):23-26.GAO Qingdi,LI Shiguang,GAO Zhengzhong,et al.Recognition mathematics based on fourier transform[J].Jourrnal of Data Acquisition&Processing,2008,23(增刊):23-26.

[3]Wang Z,Jillian G A,Miller W C.Recursive algorithms for the forward and inverse discretecosine transform with arbitrary length[J].IEEE Signal Processing Letter,1994,1(7):101-102.

[4]郑君里,应启珩,杨为理.信号与系统(第二版)[M].北京:高等教育出版社,2004:109-113.

[5]郭大钧.大学数学手册[M].济南:山东科学技术出版社,1985:541-542.

[6]ZHAO Jiguang,ZHANG Zhiquan,DENG Chen.Research on design and simulation of FM/cw lidar system[J].Laser Sensing and Imaging,2009,7 382:169-171.