基于二阶直方图的改进型均值偏移跟踪算法

陈善静,杨 华,曾 凯,杜石明,张 红

(1.脉冲功率激光技术国家重点实验室,安徽合肥 230037;2.电子工程学院,安徽省红外与低温等离子体重点实验室,安徽合肥 230037;3.电子工程学院物理教研室,安徽合肥 230037)

0 引言

近年来在目标跟踪领域,以无参数核密度估计为基础的均值偏移算法以其算法简单、收敛速度快、目标跟踪准确等优势而越来越受到大家的重视[1]。均值偏移算法又叫Mean-shift算法,是一种以目标的颜色直方图为特征的自适应梯度搜索匹配跟踪算法。它从任意一点出发,以颜色直方图的相似性最大为原则沿着核密度的梯度上升方向,以自适应的步长进行搜索[2-3],最终收敛于核密度估计函数的局部极大值处即目标的真实位置。

但是由于颜色直方图描述的是目标的全局统计信息,忽略了目标像素间的空间结构信息,当两个颜色分布相似但空间结构不一样的目标出现时,Mean-shift跟踪算法不能区别两个目标,容易导致跟踪失败。为此,学者们提出了新的改进方法。文献[4—5]提出了描述目标的特征称为空间-颜色特征,不但考虑目标像素点的颜色信息,而且还考虑像素点之间的空间关系。这种特征的跟踪算法能较好地区别目标。文献[6]提出了融合颜色和边缘信息的跟踪算法取得了较好的跟踪效果。但这种算法计算比较费时,或者被限制到单一的形状模型。文献[7]提出利用边缘方位柱状图进行跟踪,这种边缘特征计算有效而且不易受光照变化的影响,能提供比单一轮廓更丰富的特征,但是这种算法在利用Sobel算子或Prewitt算子等边缘梯度算子求边缘特征的时候,很容易受背景的影响,边缘特征十分不稳定。为了提高均值偏移算法的稳定性和抗局部遮挡能力,本文提出了基于二阶直方图的均值偏移算法。

1 均值偏移原理和二阶直方图基本概念

1.1 均值偏移基本原理

假设d维空间Rd中的样本集合{xi}i=1,…,n,在点 x处,使用有界核函数 K(x),窗半径 h的多变量核密度估计由式(1)计算

定义函数g(x)=-k′(x)。由g(x)可以导出新的核G(x)=Cg(‖x‖2),C是归一化因子。由该核函数的多变量密度估计可以推导出

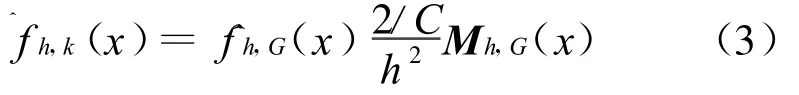
‖◦‖为欧式距离。进而可以得到核密度梯度估计

式中

式(4)被称为mean-shift向量。它表明在x处,使用核G计算的mean-shift向量正比于使用核K得到的归一化的密度梯度估计。归一化要依靠使用核G计算的x处的密度估计。因此mean-shift向量总是指向密度增大的最大方向。反复地进行如下两步,就是mean-shift过程:

1)计算 mean-shift向量Mh,G(x);

2)用Mh,G(x)平移核G(x)

1.2 二阶直方图基本概念

二阶直方图又叫空间颜色柱状图(Spatiograms),它是对颜色直方图的一种改进直方图,它以颜色直方图为基础。颜色直方图只包含了颜色分布信息,而二阶直方图在包含颜色信息的前提下包含了像素的颜色空间均值向量和颜色空间协方差矩阵。二阶直方图与颜色直方图相比不仅考虑像素点的颜色值并且考虑像素点间的空间关系,包含更丰富的目标信息。所以抗干扰性和抗局部遮挡能力更强和受光照影响更小,鲁棒性更强[8]。

颜色空间均值向量表示为:

颜色空间协方差矩阵为:

2 二阶颜色直方图对均值偏移算法的改进

2.1 颜色直方图Bhattacharyya系数

一阶颜色直方图即颜色直方图,一般而言图像像素的值域是RGB颜色空间,按照直方图的方式将RGB颜色空间的每个子空间R、G或者B空间分成k个相等的空间,每个空间称为一个bin,构成特征空间,特征空间中特征值的个数(即 bin的个数)为m=k3。

在mean-shift跟踪算法中,用Bhattacharyya系数作为相似性函数,其定义为:

δ[b(x i)-u]表示候选目标的颜色直方图特征。Bhattacharyya系数的值在0～1之间,其值越大表示两个模型越相似,如图1所示。

2.2 基于二阶颜色直方均值偏移向量

二阶直方图是一种包含了图像像素的颜色、空间分布信息的统计特征表示方法。与一阶的颜色直方图相比它包含了颜色空间均值向量和颜色空间协方差矩阵,如图2所示。

因此利用二阶直方图改进的Bhattacharyya系数可以表示为:

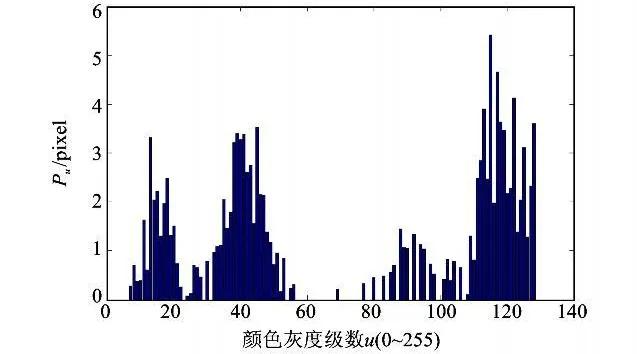
图1 颜色直方图Fig.1 Color histogram

图2 融合颜色空间分布的颜色直方图Fig.2 Color histogram fusing color spatial distribution

由基于二阶直方图的均值偏移向量可以得到目标的跟踪点为:

3 基于二阶直方图的均值偏移向量的可行性证明

由均值偏移算法跟踪算法的基本原理可知,二阶直方图的均值偏移向量只有在指向融入颜色空间均值向量和颜色空间协方差矩阵的Bhattacharyya系数梯度变化最大值时,跟踪算法才能快速收敛到跟踪目标真实位置上。因此下面我们将从理论上证明二阶直方图的均值偏移向量的方向为基于二阶直方图的Bhattacharyya系数梯度变化最大值的方向。首先对包含二阶直方图的Bhattacharyya系数在p(y0)和θ(y 0)处做二阶泰勒级数展开:

将wu代入上两式分别求导得

4 仿真验证

为了验证本文改进后算法的优越性,通过计算机编程进行了模拟实验。在实验中,电脑配置为P4 2.8 GHz CPU,512 MB内存,Windows XP操作系统和VC++6.0的开发平台。其中k=16,为了对比跟踪下效果,把mean-shift跟踪算法模块与改进后的二阶直方图跟踪算法模块做到了一个程序里。初始帧时通过手动选取视频图像中的目标建立目标模板,以后两种算法从同一坐标位置开始各自的跟踪运算。其中黑色框为使用mean-shift跟踪算法跟踪到的目标位置,白色框为使用二阶直方图跟踪算法得到的目标位置。图3为两种跟踪算法的跟踪效果对比图。

图3 Mean-shift跟踪算法与基于二阶直方图改进型跟踪算法跟踪效果对比图Fig.3 Comparative picture of mean-shift tracking algorithm and the improved tracking algorithm based on second order histogram tracking effect

通过观察对比图3两种跟踪算法的效果图可以发现:

1)基于二阶直方图的改进型mean-shift跟踪算法的抗局部遮挡能力明显比未改进的mean-shift算法抗局部遮挡能力强。

2)在图3的第140帧处跟踪目标已经大部分被书遮挡,此时的mean-shift跟踪算法整个跟踪区域内只有小部分真实目标颜色相近,整个 Bhattacharyya系数受到较大影响,降低到0.4～0.5左右,不能准确定位目标。基于二阶直方图的改进型mean-shift跟踪算法此时在跟踪区域内也只有较小的一部分真实目标颜色相近,这块小的蓝色目标区域集中分布在跟踪框的左下部,而选择的目标模板的左下部同样为蓝色,此时跟踪框左下部区域与模板左下部区域正好匹配,在程序中由颜色空间均值向量和颜色空间协方差矩阵所决定的w u对Bhattacharyya系数进行了修正,提高了Bhattacharyya系数的数值,增加了定位的准确性。

3)在图3第180帧是可以看到使用wu修正后的Bhattacharyya系数即使在只有很小的一块区域与模板颜色相同且此区域空间分布与模板相近时跟踪框都能跟踪上目标。

4)在图3第280帧时可以看到基于二阶直方图的改进型 mean-shift跟踪算法同样保持了 meanshift算法优良的收敛性,当遮挡消失后跟踪框能很快地移动到跟踪目标上,准确地跟踪目标。

通过观察对比图4—图6两种跟踪算法中的Bhattacharyya系数随时间变化和在140帧图像时Bhattacharyya系数空间分布可以发现:

1)图4为Bhattacharyya系数随时间变化曲线,从图中可以看出,在100帧处,跟踪目标开始被桌面的书部分遮挡,传统的mean-shift跟踪算法的Bhattacharyya系数在此时快速下降,当基于二阶直方图的mean-shift跟踪算法由于包含颜色空间分布信息,即使被严重遮挡时候Bhattacharyya系数变化也比较小。

2)图5、图6为第140帧时目标区域Bhattacharyya系数空间分布情况图,由图3可见,在第140帧时目标受到严重遮挡,传统的mean-shift跟踪算法的Bhattacharyya系数在目标区域普遍较低,而基于二阶直方图的mean-shift跟踪算法的Bhattacharyya系数融合了颜色空间均值向量和颜色空间协方差矩阵因此在此情况下目标区域数Bhattacharyya系数值下降不是很大,Bhattacharyya系数曲面的峰值比较明显,有利于提高跟踪的稳定性和抗遮挡能力。

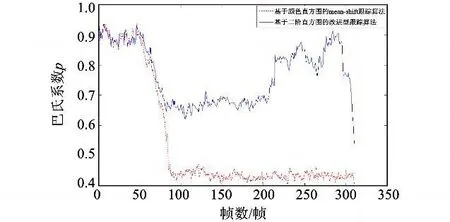
图4 两种跟踪算法Bhattacharyya系数变化曲线Fig.4 Two curves of Bhattacharyya coefficient for both tracking algorithms

图 5 mean-shift跟踪算法在第140帧时目标区域Bhattacharyya系数分布图Fig.5 Bhattacharyya coefficient distribution of mean-shift tracking algorithm in the target area in the 140th

图6 基于二阶直方图的改进型跟踪算法在第140帧时目标区域Bhattacharyya系数分布图Fig.6 Bhattacharyya coefficient distribution of improved tracking algorithm based on second-order histogram in the target area in the 140th

5 结论

本文应用二阶直方图改进了均值偏移跟踪算法,在颜色直方图中引入了颜色空间均值向量和颜色空间协方差矩阵,使颜色直方图不仅包含了目标的颜色信息还包含了目标颜色的空间分布的信息。仿真表明:改进后的均值偏移算法具有更强的抗遮挡能力,对目标跟踪更加准确稳定。

[1]虞旦,韦巍,张远辉.基于多特征空间的均值漂移算法[J].模式识别与人工智能,2009,22(4):666-672.YU Dan,WEI Wei,ZHANG YuanHui.Mean shift tracking algorithm based on multi-feature space[J].PR&AI,2009,22(4):666-672.

[2]常发亮,赵瑶,陈振学,徐建光.基于Mean Shif t和自适应预测的非刚性目标跟踪算法[J].控制与决策,2009,24(12):1 821-1 825.CHANG Faliang,ZHAO Yao,CHEN Zhenxue,XU Jianguang.Non-rigid object tracking algorithm based on mean shif t and adaptive prediction[J].Control and Decision,2009,24(12):1 821-1 825.

[3]Comaniciu D,Ramesh V,Meer P.Kernel-based object tracking[J].IEEE Transaction on Pattern Analysis and Machine Intelligence,2003,25(5):564-577.

[4]Yang C,Duraiswami R,Davis L.Efficient mean-shift tracking via a new similarity measure[C]//Proceedings of IEEE Computer Society Conference on Computer Vision and Pattern Recognition.San Diego,CA,United States:IEEE,2005:176-183.

[5]Wang H,Suter D,Schindler K.Effective appearancemodel and similarity measure for particle filtering and visual tracking[C]//Proceedings of 9th European Conference on Computer Vision.Graz,Austria:2006:606-618.

[6]Perez P,Vermaak J,Blake A.Datafusion for visual tracking with particles[J].Proceedings of the IEEE,2004,92(3):495-513.

[7]Yang C,Duraiswami R,Davis L.Fast multiple object tracking via a hierarchical particle filter[C]//Proceedings of IEEE International Conference on Computer Vision.Beijing,China:IEEE,2005:212-219.

[8]Birchfield S T,Rangarajan S.Spatiograms versus histograms for region-based tracking[C]//Proceedings of IEEE Computer Society Conference on Computer Vision and Pattern Recognition.San Diego,CA,United States:IEEE,2005:1 158-1 163.