无碴轨道精密定轨测量

朱文华 覃爱丽

就有碴轨道而言,无碴轨道突出的特点之一就是轨道的高平顺性,它直接限制列车的运行速度。为满足轨道的高平顺性,线路必须符合非常准确的集合线形参数,误差必须保持在毫米的范围内,对定轨测量进度要求很高,须达到这一高精度要求(主要技术标准是:10 m弦长的轨道高低偏差为±2 mm,轨向±2 mm;150 m弦长的轨道高低偏差为±10 mm,轨向±10 mm)。

1 精密定轨测量的依据

轨道必须采用绝对定位与相对定位测量相结合的铺轨测量定位模式。现行的《新建铁路工程测量规范》《既有铁路工程测量规范》有碴轨道铁路各级控制网测量的精度指标,主要是根据满足线下工程的施工控制要求而制定的,没有考虑轨道施工对测量控制网的精度要求。轨道的铺设是按照线下工程的施工现状,采用相对定位的方法进行铺设,即轨道的铺设是按20 m弦长的外矢距来控制轨道的平顺性,没有采用坐标对轨道进行绝对定位。相对定位的方法能很好地解决轨道的短波不平顺性,而对轨道的长波不平顺性无法解决。对时速大于200 km的铁路,曲线半径大且长,如果仅采用相对定位的方法进行铺轨控制,而不采用坐标进行绝对控制,轨道的线形不能满足设计要求。曲线外矢距的计算式为:

其中,C为弦长;R为半径。800 m的曲线,铺一个半径为2 800 m轨时若按10 m弦长3 mm的轨向偏差来控制曲线,当轨向偏差为0时,R=2 800 m;当轨向偏差为+3 mm,R=2 397 m;当轨向偏差为-3 mm,R=3 365 m。这个问题在既有线时提速改造中已暴露出来,即一个长曲线由几个不同半径的曲线组成,且半径相差几百米。对于10 m弦长,只采用10 m轨向偏差来控制轨道的平顺性是不严密的。

2 精密定轨测量控制要求[1]

《客运专线铁路无碴轨道工程测量技术暂行规定》对无碴轨道的平面和高程控制进行了新规定,主要归纳如下。

2.1 平面控制测量要求

平面按照三级控制布网:一级为基础控制网,二级为线路控制网,三级为基桩控制网,其要求见表1。

表1 各级平面控制网布网

2.2 高程控制测量要求

铁路无碴轨道高程控制网主要针对水准基点和控制基桩:要求一般在2 km之内埋设1个水准基点,其精度按照二等水准精度及技术要求进行测设;控制基桩按照精密水准介于二等水准与三等水准精度之间精度及技术要求进行测设。加密基桩是在控制基桩基础上加密,根据不同的无碴轨道形式,按照精密水准测量要求执行。

2.3 坐标系统与投影变形[2]

由于客运专线无碴轨道精度要求较高,因此规定平面坐标系统适合于采用工程独立坐标系统,对边长投影变形,规定在10 mm/km之内。对于与国家坐标系统的联系,需要引入并建立坐标转换关系,主要是为了地方政府规划、土地征用等使用,施工使用工程独立坐标系统。

3 无碴轨道精密定轨计算模式[3,4]

地面点与线路的相对关系,可以通过两个量和一个边向确定:两个量为地面点在线路中的里程 LP和地面点距线路中线的距离DP;一个边向是指地面点在线路中线的哪一边。如果按线路前进方向视准时,地面点在线路中线左侧则称为左边,地面点在线路中线右侧则称为右边。如果规定地面点位于线路左边、右边时,所求距中线距离DP的符号有正负之分,这样就可以用DP的正负号来表示左右边。按照惯例,当地面点位于中线左边时,DP取负值,反之DP取正值;显然,也可以用DP的正负性来判断地面点相对于线路的边向。因此,地面点与中线的相对关系可以通过地面点在中线上的里程L与带有正负号的距中线距离DP表示(见图1)。

此点在过渡坐标系的切线方位角为:

则过此点切线的方程为:

把式(2),式(3)代入式(5)得:

把cotβ按级数展开,得:

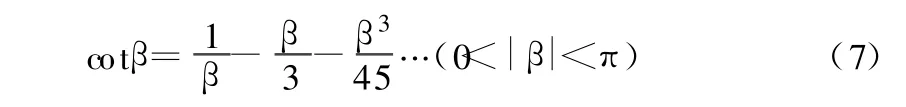
然后把β代入式(6),又得:

根据牛顿迭代法公式

根据上面所得公式,在计算过程当中,一般首先给定初始位置坐标(x,y)以及缓和曲线长度,程序流程图如图2所示。

利用一个简单的计算题目进行牛顿迭代,求2×x×x×x-4×x×x+3×x-6=0在1.5附近的根,程序流程分析:

1)赋值 x0=1.5,即迭代初值;

2)用初值 x0代入方程中计算此时的 f(x0)及 f′(x0),程序中用变量f描述方程的值,用 fd描述方程求导之后的值;

3)计算增量 d=f/fd;

4)计算下一个 x,x=x0-d;

5)用新产生的x替换x0,为下一次迭代做好准备;

6)若 d绝对值大于1e-3,则重复2),3),4),5)步。

源程序代码:

4 结语

本文给出的地面点解算方法便于计算机编程,适当拓展高次项及缩小解算过程趋近限差,可以大大提高解算精度,满足精密工程的要求。该方法的计算公式和逻辑判断简单,易于程序实现,且无需增加额外测点,因此更具实用价值。

[1] 秦世伟,陈小枚.快速确定交通路线加桩的简要方法探讨[J].测绘通报,2001(2):40-45.

[2] 宋 文.路线中桩放样新方法[J].工程勘察,1989(6):40-42.

[3] 李青岳.工程测量学[M].北京:测绘出版社,1984:78-81.

[4] 许 曦,刘庆元,余加勇.基于牛顿迭代法缓和曲线加桩计算[J].测绘通报,2004(4):20-22.