无线传感器网络定位算法综述*
黄 毅,胡爱群
(东南大学信息科学与工程学院 南京210096)
1 引言
位置信息对于无线传感器而言是非常重要的,一个没有传感器节点位置信息的WSN(无线传感器网络)是没有应用意义的,因为几乎所有的WSN应用场合都需要知道节点位置信息,比如:动物种群的跟踪研究,大楼火灾的预警,仓库中货物的管理,交通监控系统等。一个直接的方法是在节点上安装GPS,但是由于WSN是由成百上千甚至更多的传感器节点组成的,成本太高,而且它需要长距离通信,能量花费也很高,体积很大;也不能运用在室内,所以这种方法不适合用于WSN的定位。
多年来,很多国内外学者和研究机构针对WSN的特点——能量有限、价格低廉、自组织性、无线通信、多跳中继、分布式处理、容错性等,展开了深入的研究并提出了很多的定位算法。本文对无线传感器网络节点的坐标计算方法和国内外开展的定位算法研究工作进行了介绍和归纳,可供读者在WSN的深入研究与应用中参考。本文把定位算法划分成两个类别:需要/不需要测距,而每种算法又兼有以下一种或几种特点:需要/不需要锚节点(已知坐标的节点)、集中式/分布式、固定/移动等,这些在具体算法中会特别说明。
由于固定WSN的定位算法能扩展到移动的WSN中,所以这里主要以固定WSN的定位算法为主要内容,然后再介绍移动情况下的定位算法。
2 定位算法
首先,介绍一下常用的坐标计算方法。
(1)三边测量术
三边测量术是根据3个已知坐标的节点到未知节点的距离来确定节点坐标。已知A、B、C三个节点的坐标分别为(xa,ya)、(xb,yb)和(xc,yc),它们到未知节点 D(x,y)的距离分别为 da、db和 dc,如图 1(a)所示,则通过计算可以得到以下三个式子:
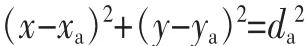

通过高斯消元法可以得到以下两个式子:

写成矩阵形式AX=b:

那么X=A-1b,注意的是A要可逆的充要条件是A、B、C三点不共线。
(2)三角测量术
三角测量术常用到基于AOA方法的测距中,它根据三个已知坐标的节点到未知节点的相对角度来确定节点坐标。已知A、B和C三个节点的坐标分别为(xa,ya)、(xb,yb)和(xc,yc),假设节点 D 的坐标为(x,y),如图 1(b)所示。对于节点A、C和D,如果弧段AC在△ABC内,那么能够惟一确定一个圆,并存在下列公式:
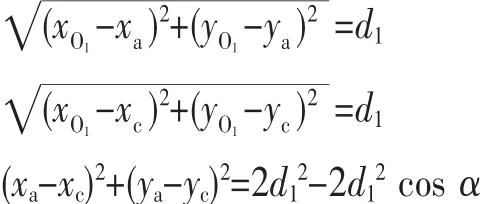
上式中,d1为圆半径,O1为圆心,α为圆心角∠AO1C。
由以上三式能够确定圆心O1点的坐标和半径。同理可对A、B、D和B、C、D分别确定相应的圆心和半径,最后利用三边测量术确定D的坐标。
(3)多边测量术
多边测量术(多角可以化为多边)是根据n个已知坐标的节点到未知节点的距离来确定节点坐标的。已知n个节点的坐标分别为(x1,y1)、(x2,y2),…,(xn,yn),它们到未知节点D的距离分别为 d1,d2,…,dn,假设节点 D的坐标为(x,y),可以列出n个等式,形式如三边测量术中描述,通过计算可以得AX=b。使用标准最小均方差估计方法可以得到节点D的坐标为:

这种方法充分利用了节点所收集到的定位信息,所以在很多定位算法中都有应用。如果考虑多径和噪声的影响,一种更为符合实际情况的变形如下[1]:
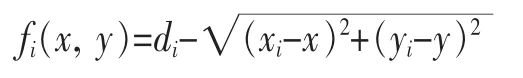
求使得下式达到最小的解即为所求坐标。

αi是第i个信号的权值,与实际信道有关。
2.1 需要测距
如果要采用以上三种坐标的计算方法,那么必须知道一个未知节点到至少三个锚节点的距离(角度信息也可以化为距离信息)。常用的 4种测距方法为:RSS(received signal strength)、TOA(time of arrival)、TDOA(time difference

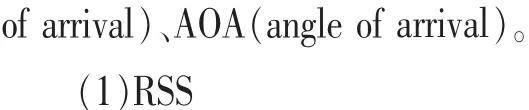
通常情况下无线电波或声波信号在介质中传输时,信号功率是随传播距离的变大而衰减的,这是RSS测距的理论基础。针对无线电波信号传播的信道,一般采用的模型如下式所示:
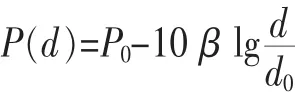
其中,d是离开信号发射源的距离,P0是在距离信号发射源d0点(记为N点)的信号接收功率,β是路径损耗系数,根据环境的不同,通常为2~6。在参考点N处的功率是通过预测已知的,这样通过接收信号的强度即可判断距离d。
(2)TOA
TOA也可以叫做TOF(time of flight)。速度一定的情况下,检测信号从发送到接收到的时间即和距离成正比,这种方法需要时钟的同步。
(3)TDOA
TDOA可以分成两种情况。①两种速度不同且相差很大的信号,如无线电信号和超声波信号,由于无线电波速度很快,一般情况下可以看成即时到达,而声波传输相对就慢很多,在节点上同时安装以上两种信号的接收装置,检测到两信号到达的时差,就可以计算出距离。这种方法可以避免同步,但由于要多安装一种信号的接收装置,成本和通信开销相对较大。②同一种信号到达每个锚节点的时差,这种方法需要每个锚节点的时钟同步。
(4)AOA
这种方法需要角度信息,而角度信息主要依靠在节点上安装天线阵列来获得,再通过三角测量术算出待定位节点坐标。AOA方法需要天线阵列,成本和能耗是两个很大的问题,对于WSN来说AOA的实用性也较差。
表1[2]是各种现有的定位系统的相关信息,包括采用的技术和能达到的精度。
从表1中可以看出,大部分的定位技术不能直接应用到WSN中去,但是关键的测距技术是可以借鉴的。
2.2 不需要测距
在这类算法中假设节点只能和它邻近的节点进行通信,也就是说只能和在其有效的通信距离内的节点进行通信,借助网络信息可以从两个较远的节点通过多跳(multihop)的方式传送。通过对跳数信息的处理可以估计出两个节点间的距离,再通过相应的算法得到节点的位置。
(1)DV-hop
基于通信跳数的DV-hop算法是由NiCuleScu提出来的[3]。它的提出有两个假设:①在一个大型网络中,一个待定位节点可能无法与足够多的锚节点直接通信;②在利用空中抛洒的方式对未知区域进行监控时,只可能少数的锚节点有预知的坐标信息,如安装了GPS的锚节点,而其他节点通过中继的方式和锚节点通信。它的基本原理是用跳段距离来代替节点间的实际距离。

表1 现有定位系统的各种相关信息

上式中,ci是锚节点i的跳段距离,分子部分是锚节点i到其他锚节点的欧式距离之和,分母部分是锚节点i到其他锚节点的跳数之和。待定位节点到锚节点i之间的距离估计通过下式得出:
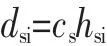
cs表示待定位节点采用的跳段距离,hsi是待定位节点s和锚节点i之间的最小跳数。算出至少三个距离(2D),利用前面的极大似然估计,就可以估计出节点坐标。
DV-hop算法的优点很多,属于分布式算法,算法简单,通信开销少,计算量也少,利用跳数信息代替精确测距,硬件设计也简单,成本也低廉;不足是对网络节点的密度依赖性较大——密度越大,定位精度越高,所以它不适用于非凸区域,当有障碍物时,跳数信息不能正确反映实际距离。参考文献[4]结合RSSI来减小误差,参考文献[5]使用节点到邻节点的测距来提高多跳距离的精度,这些都需要额外的硬件开销。参考文献[6]通过待定位节点和锚节点间距离限制来改善定位精度。
(2)AFL
NISSanka[7]等人提出的 A FL(anchor-free localization)算法是一种无需锚节点的定位方法,它分为两步:首先,通过多跳确定一个相对坐标系,得到每个节点在这个坐标系中的位置坐标,然后,通过质量—弹簧(Mass-Spring)模型进行迭代优化。具体步骤如下:第一步,初始随机选择一个节点n0,然后选取一个距离其最大的点n1;再选取一个距离n1最大的点 n2;接着选 n3,使得|h13-h23|最小(hij表示节点i、j之间的最小跳数),如果有多个点,则选h13+h23最大的点;类似的选取n4,使得|h14-h24|最小,如有多个,则选h34最大的点;最后选取n5点,满足|h15-h25|最小,如有多个点,则选取|h35-h45|最小的节点。这样,选取的5个点能够组成一个临时的坐标系:以n5为原点,其余4个点为4个方向上的端点。那么,网络中的每个点就有一个对应的坐标,如用极坐标(ρi,θi),ρi=rhi,5,θi=tan,这里r为通信半径。这样得到的是每个节点的粗略坐标。第二步,再用质量—弹簧模型进行迭代优化,把点与点之间的实际测量距离看成是弹簧的平衡位置,那么根据之前的估计距离与实际距离之差,可以得到弹簧是被缩小了,或是被拉伸了,这样整个网络就存在能量,如图2所示,我们的目标就是使得这个能量最小,那么调整后的节点坐标即为优化后的坐标。这个算法的好处是:无需锚节点和分布式。但在质量-弹簧优化阶段,需要实测距离,这就限制了此方法的应用。还有一个问题是迭代收敛的问题,很可能网络收敛到一个局部最优点,而不是全局最优,对此目前没有很好的解决方法。图2中O为系统无能量时的节点位置,O’为系统存在能量时的节点位置。
(3)MDS
MDS(multidimensional scaling)只是流形学习(manifold learning)方法其中的一种,它和 P CA(principal component analysis)、ISOMAP (isometric feature mapping)、LLE(locally linear embedding)等构成常用的流形学习方法[8]。在参考文献[9]中,作者提到了流形学习能够用来处理网络定位问题。Y.Shang和 W .Ruml[10,11]利用 M DS 来 解决 W SN 中 的节点定位问题。这种方法可以不需要测距(也可以需要),利用在有效通信距离内的两两节点之间的相似度来进行定位,比如:连通度或欧式距离,我们泛称它们为距离。设Xi=(xi1,xi2,…,xim)是m维空间上的一个点表示i、j两点的距离,在一个有 n 个节点的 W SN中,有 n ×n个距离,可以组成一个平方距离矩阵A,由A可计算B=-HAH/2、XTX,其中 H =I-11T/N,1=(1,1,…,1)T,由于 B 是对称且半正定的,所以存在奇异值分解B=UΛUT=XTX,则有X=Λ1/2UT,其中 Λ =diag(λ1,…,λr),r=rank(B),λ1≥λ2≥…≥λr为B的正特征值,U的列向量由与λ1≥λ2≥…≥λm相应的标准正交向量组成。对于WSN中2D和3D的情况,只要r取2或3即可。这只是得到了n个节点的相对位置坐标,如果有3个(3D是4个)或更多个锚节点坐标,通过坐标变换,可以得到所有节点的绝对坐标。这个算法的优势是可以不需要锚节点,而且在锚节点较少的规则网络中,也可以达到较好的效果,不足是算法较复杂,仅奇异值分解这一关键步骤就需要O(n3)的复杂度。之后也有人提出基于MDS的改进定位算法,如参考文献[12]把整个网络划分成多个局部,对每个局部进行定位,再融合到全局中去,实现了分布式的计算。参考文献[13]利用最短距离作为测地线距离代替欧式距离来实现定位,提高了精度,但是邻近参数K的选择较复杂。

(4)基于区域的定位算法
此类算法是通过划分局部的节点区域来实现定位,也不需要测距,主要有质心Centroid算法、APIT算法、基于Voronoi图算法[14]等。
质心Centroid算法[15]:把节点周围多个(2D至少3个)锚节点组成一个多边形,它的质心估计成节点的位置,如图3(a)所示,因此,多边形的面积越小,估计误差会越小,此算法要求锚节点的密度很大且均匀分布,一般情况下,WSN达不到这种要求。但是,这种算法非常简单,很容易在节点上实现,适用于定位精度不高的场合,同时,它也是分布式的算法。参考文献[16]提出了基于权重的质心算法即加权质心算法(W-Centroid),加权质心算法引入接收信号强度来代替质心算法中的连通性,对于接收信号强度较大的锚节点就具有较大的权值。

图3 基于区域的定位算法
APIT算法[17]:实际上它是质心算法的改进,它选取有效通信距离内的所有锚节点中的三个(2D)组成一个三角形,用检测信号能量的方法判断节点是否在三角形中,这样,依次判断每三个锚节点组成的三角形,最后,它们的交集即是节点所在的区域,如图3(b)所示。相比基本的质心算法,它有着更小的有效区域,所以也能够达到更高的定位精度。由于是质心算法的改进,所以质心算法的缺点它也存在。
此外,还有类似的算法:SBL(sequenee-based loealization)[18]、SDP (semi-definite programming)[19]、 基 于Voronoi图算法等,都是基于区域的思想。
3 移动节点定位
移动无线传感器网络(mobile wireless sensor network,MSN)的定位问题越来越受到人们的关注,由于节点的移动,定位的精度也会随着移动速度的增大而降低,同时,又能获得更多的位置信息来定位。在某些方面,移动机器人(mobile robot,MR)和 MSN有着相似之处,因此很多在MR中的定位算法可以移植到MSN中去,但是,MSN又有着自身的特点——计算和通信能力较弱,复杂的算法不可能运用到MSN中去。一种简单有效的MSN定位算法MCL(Monte Carlo localization)[20]被广泛研究。
Monte Carlo方法是冯·诺依曼在“曼哈顿计划”中命名的一种计算机随机模拟方法。L.Hu和 D.Evans[21]提出的MCL算法,是运用在移动网络中的节点定位算法,它的关键思想是用一组随机的带权值的采样点逼近节点可能的后验分布,节点的位置由采样点和权值确定。MCL把时间分成离散的单元,在每个单元中估计节点的位置,计算过程由两部分组成:预测和过滤。在预测阶段,依据节点之前的位置lt-1和最大移动速度vmax(一个时间单元内的最大移动位移),将t时刻的节点的可能位置限制在一个以lt-1为圆心、半径为vmax的圆内,在这个圆内随机选择一个位置作为节点位置采样。然后进入过滤阶段,节点观察它所有的邻锚节点并和它们进行信息交换,找寻所有一跳(dsi A.Baggio和K.Langendoen提出一种改进的MCL算法,称为 MCB(Monte Carlo localization boxed)[22]。它的主要改进是把采样区域限制在一个最小的有效范围之内,使得估计的位置精度更加准确,而且还降低了计算开销,这个区域被称为锚节点盒或采样盒,如图4所示。在参考文献[23]中利用了距离信息的MCL算法来提高估计精度,但是精度的改善是以增加通信开销为代价的。参考文献[24]中,一种二重的混合MCL被提出,精度进一步提高,但计算开销也进一步增加。在WSN中,计算有效性是一个很重要的衡量标准,节点的简约性决定了不可能有很强的计算能力,而在MCL中,主要的计算量取决于采样个数的大小,由此参考文献[25]提出了一种可变采样数的MCL算法,既可以达到MCL相同的精度,又减少了计算开销。 由于节点的移动性,移动节点本身可以提供定位信息,如在三个时刻与待测节点的测距可以确定这个节点的坐标,可以避免多跳和远距离测量的误差,因此,移动节点的路径规划就显得很重要。 定位算法随着WSN的发展而不断发展,本文根据定位算法的特点,分类讨论了目前主流的定位算法和它们的一些改进,但是,还有很多问题没有解决,如能耗、同步、测距干扰、网络优化、非凸区域等,都需要进一步改善。未来的研究方向可以从以下几个方面考虑:方法的融合、智能天线、网络的拓扑结构、模式识别等。 1 Turin George L,Jewell William S,Johnston Tom L.Simulation of urban vehicle-monitoring systems.IEEE Transactions on Vehicular Technology,VT-21,Feb 1972 2 Zafer Sahinoglu,Sinan Gezici,Ismail Guvenc.Ultra-wideband positioning systems.Cambridge,Massachusetts,USA,Cambridge University Press,2008 3 Niculescu Dragos,Nath Badri.Ad hoc positioning system(APS).In:Conference Record /IEEE Global Telecommunications Conference,San Antonio,TX,United states 2001 4 Li Xiaoli,Shi Hongchi,Shang Yi.A partial-range-aware localization algorithm for ad-hoc wireless sensor networks.In:Proceedings of the 29th Annual IEEE International Conference on Local Computer Networks (LCN'04),Tampa,FL,United States,Nov 2004 5 Savarese,Rabaey J,Langendoen K.Robust positioning algorithm for distributed ad-hoc wireless sensor networks.In:USENIX Technical Annual Conference,Monterey,CA,June 2002 6 Ji Weiwei,Liu Zhong.An improvement of DV-Hop algorithm in wireless sensor networks.In:2006 International Conference on Wireless Communications,Networking and Mobile Computing,WiCOM 2006,Wuhan,China,2006 7 Priyantha Nissanka B,Balakrishnan Hari,Demaine Erik,et al.Anchor-free distributed localization in sensor networks.In:Proceedings of the First International Conference on Embedded Networked Sensor Systems,Los Angeles,CA,United States,2003 8 陈维桓.微分流形初步 (第二版).北京:高等教育出版社,2001 9 Patwari N,Hero A,III.Manifold learning algorithms for localization in wireless sensor networks.In:Acoustics,Speech,and Signal Processing,2004 (ICASSP’04),Montreal,Que,Canada,May 2004 10 Shang Yi,Ruml Wheeler,Zhang,Ying,et al.Localization from mere connectivity. In: Proceedings of the International Symposium on Mobile Ad Hoc Networking and Computing(MobiHoc),Annapolis,MD,United States,June 2003 11 Shang Yi,Ruml Wheeler.Improved MDS-based localization.In:IEEE INFOCOM,Hongkong,China,March 2004 12 Ding Yingqiang,Du Liufeng,Yang Ting,et al.Distributed localization algorithm for wireless sensor network based on multidimensional scaling and the shortest path distance correction.Transactions of Tianjin University,2009,15(4):237~244 13 Wang Chengqun,Chen Jiming,Sun Youxian,et al.Wireless Sensor Networks Localization with Isomap.In:ICC'09,Dresden,Germany,June 2009 14 Jiang Jie,Song Zhen,Zhang Heying,et al.Voronoi-based improved algorithm for connected coverage problem in wireless sensor networks.Lecture Notes in Computer Science(including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics),v3824 LNCS,2005,Embedded and Ubiquitous Computing-International Conference EUC 2005,Proceedings,Nagasaki,Japan,Dec 2005 15 Bulusu Nirupama,Heidemann John,Estrin Deborah.GPS-less low cost outdoor localization for very small devices.IEEE Personal Communications,7(5):28~34 16 Shen Xingfa,Wang Zhi,Jiang Peng,et al.Connectivity and RSSI based localization scheme for wireless sensor networks.In:Advances in Intelligent Computing,International Conference on Intelligent Computing(ICIC 2005),Hefei,China,2005 17 He Tian,Huang Chengdu,Brian M.Blum,et al.Range-free localization schemes for large scale sensor networks.In:ACM International Conference on MobileComPutingandNetworking(MobiCom),SanDiego,Califomia,USA,2003 18 Yedavalli Kiran, Krishnamachari Bhaskar. Sequence-based localization in wireless sensor networks.IEEE Transactions on Mobile Computing,7(1):81~94 19 Biswas Pratik,Ye Yinyu.Semidefinite programming for ad hoc wireless sensor network localization. Third International Symposium on Information Processing in Sensor Networks(IPSN 2004),Berkeley,CA,United States,2004 20 Yuan Liang,Chen Weidong,Xi Yugeng.A review of control and localization for mobile sensor networks.In:Proceedings of the World Congress on Intelligent Control and Automation(WCICA),Dalian,China,June 2006 21 Hu Lingxuan,David Evans.Localization for mobile sensor networks.In:Proc of MobiCom 2004,Philadelphia,PA,USA,Sept 2004 22 Aline Baggio,Koen Langendoen.Monte-Carlo localization for mobile wireless sensor networks.In:Proc of Mobile Ad-hoc and Sensor Networks,Second International Conference,MSN 2006,Hong Kong,China,Dec 2006 23 Dil Bram, Dulman Stefan, Havinga Paul. Range-based localization in mobile sensor networks.Lecture Notes in Computer Science(including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics),v3868 LNCS,2006,Wireless Sensor Networks-Third European Workshop,EWSN 2006,Proceedings,Zurich,Switzerland,Febrary 2006 24 Enrique Stevens-Navarro,Vijayanth Vivekanandan,Vincent W S Wong.Dual and mixture Monte Carlo localization algorithms for mobile wireless sensor networks.In:Proc of IEEE Wireless Communications and Networking Conference (WCNC'07),Hong Kong,China,March 2007 25 Wang Weidong,Zhu Qingxin.Varying the sample number for Monte Carlo localization in mobile sensor networks.In:Proceedings-2nd International Multi-Symposiums on Computer and Computational Sciences(IMSCCS'07),Iowa City,IA,United States,August 2007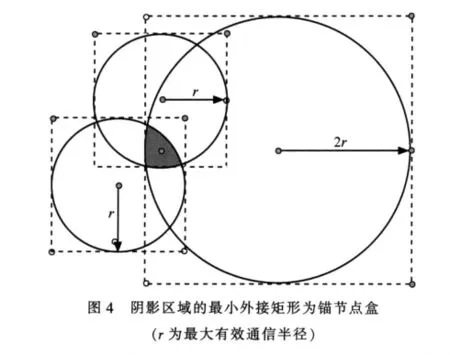
4 结束语

