基于ACE的准循环LDPC码构造

李继龙

（国家广播电影电视总局 广播科学研究院，北京 100866）

责任编辑:哈宏疆

1 引言

低密度奇偶校验（Low Density Parity Check，LDPC）码以其优秀的性能受到学术界的关注与广泛研究。目前在DVB-S2、IEEE802.16e以及中国的数字电视地面广播、数字电视卫星广播、移动多媒体广播等标准中，都采用了LDPC码。

LDPC码的性能与码长息息相关，码长越长，其性能越好。但是在实际应用中，为降低硬件实现复杂度和成本，码长可能受到限制。密度进化可得到非规则LDPC码的最优度序列的设计，获得最大译码器阈值，从而得到最佳译码性能。但是仅仅基于最优度分布设计的有限码长LDPC码的性能并不理想。LDPC码设计中要最大化围长，短的围长会恶化迭代译码的性能。在有限码长LDPC中，由于码长平均环长和码长成对数关系，围长长度将受限于码长。LDPC码设计中的另外一种设计思路是减少对应双向图中小的停止集。小停止集对二进制删除信道（BEC）中的迭代译码是有损害的。在高斯信道中减少小停止集可以达到同样的效果[1]。

本文首先分析了LDPC码的结构类型和译码实现，确定采用QC-LDPC码作为纠错编码，利于实现时采用半并行结构。然后分析了LDPC码的性能限制因素，着重分析了停止集对误码性能的影响。之后，提出基于ACE（Approximate Cycle EMD）的准循环LDPC码构造算法。最后，通过仿真分析验证了本文所提算法的有效性。

2 LDPC码结构类型和译码实现分析

采用随机LDPC码可获得良好的编码增益，长的随机LDPC码的性能接近香农限[2]。但是随机LDPC码没有结构化LDPC码的结构特点，其编码需要的硬件比结构化LDPC码的编码远为复杂；多进制LDPC码的优异性能改善是以增加译码复杂度为代价，译码复杂度相当高，不利于硬件的实现；准循环LDPC码可用简单线性移位寄存器完成编码，准循环的特点使其能节约存储空间，可以采用分层译码的方式，进行并行译码，减少了译码时延，硬件实现复杂度低[3-6]。

在码构造时必须考虑利于译码实现，LDPC译码器主要有3种实现结构:完全并行结构、串行结构和部分并行结构。完全并行的译码结构中所有的变量节点和校验节点的更新处理在一次迭代过程中完成，具有很高的吞吐量，但是占用的资源会随着数据块长度的增加而快速增加；串行译码结构一次迭代只处理一个变量节点和一个校验节点处的概率更新，因而占用的资源很少，但是数据吞吐量非常低；部分并行译码结构要求校验矩阵具有一定的规律性，功能单元通过时分复用来减少资源面积的耗用，每次迭代处理一定数目的比特节点和一定数目的校验节点处的概率更新。半并行结构可平衡译码的复杂度和处理时延，是译码实现的最佳结构。QC-LDPC码的结构特点适合于半并行结构的实现。

QC-LDPC码可以通过紧凑的指数矩阵M（H）来表示，其大小为 m×n，其中 n×p是 LDPC码的码长，m×p是校验位数，p是循环移位矩阵的大小。指数矩阵表示为

校验矩阵H可以由指数矩阵M（H）扩展得到，将[-1，p-1]内的循环移位值 Pi，j扩展为扩展阵 QPi，j。 扩展阵QPi，j表示一个p×p的循环置换矩阵，它是由单位矩阵的每一行循环右移位Pi，j位得到的。

3 LDPC构造分析

LDPC码纠错性能的约束条件包括了4个方面:1）码长越长，性能越好；2）非规则码的节点度数分布优化；3）尽量减少码中的短循环；4）双向图中连接的伸展性。其中码长与实际应用有关，而节点度数分布通过密度进化得到。

LDPC码在实际应用中，码长可能受限。中短码长的LDPC码由于码长限制，短环出现的几率更大[3]。LDPC码的消息传递译码算法假定变量节点是相互独立的，短环的存在必然破坏了独立性的假设，使得译码性能明显下降。短环的存在使得变量节点在迭代译码的过程中频繁给自己传递正反馈信息，这对于迭代译码而言是不希望出现的。因此，一般的码构造方法都尽量避免短环的存在。

PEG基于环的算法以增长LDPC码环长为目标。但是校验矩阵双向图中的短环对误码性能的影响并不一致，并不是环长越小对译码性能的影响就越大。环长稍长但与剩余图连通性较差的环对译码性能的影响比环长稍短但与剩余图连通性较好的环大，这是由于双向图中连接性高的环中的信息节点在错误接收时通过迭代译码过程易于被相邻节点校正，从而降低错误信息的迭代译码过程中的传播，使之能够被正确译码。

研究分析表明，LDPC码在高信噪比时，误码平台产生的主要原因是BP译码算法作用在双向图中的某种拓扑结构而产生了无法自纠正的错误——停止集。停止集中的校验节点连接至停止集内的变量节点集至少2次。当停止集中的变量节点处于错误状态时，这些错误将会在接下来的迭代译码过程中传播，若停止集内校验节点数量少，则返回的信息中没有新的信息，不足以纠正变量节点的错误时，译码器就始终陷于一个错误的状态，无法自纠正。分析表明LDPC码的误码平台主要由停止集的大小和分布决定，为降低误码平台，需要构造好的拓扑结构，避免停止集的出现。中短码长的LDPC码短环出现的几率更大，因而中短LDPC码中小停止集出现的几率更大，从而影响误码平台。

通过避免小的停止集可有效提高不规则LDPC码的纠错性能，但是在构造过程中直接搜索并减少小停止集的方法不易实现。一种简便的方法是使变量节点集有更多的外部节点，从而可避免码中的小停止集。变量节点集的外信息度（Extrinsic Message Degree，EMD）是该变量节点集中外来约束节点的数目。EMD描述了环和双向图中其他节点的连接性。

传统的构造算法通过增大环长减少了小停止集，有两个原因。首先，较长的环必然包含许多变量节点，因而相应停止集较大。其次，若连通图无短环，则其EMD也较大。但是对于有限码长LDPC，由于不能消除所有短环，需要通过增大码中的EMD来排除连接性小的短环，从而增大最小停止集。在高信噪比时，这样的结构对纠错非常重要。

在计算环的EMD时，要判定相邻节点是否在停止集中其他任意环内，这就需要耗时的计算判定。如果忽略上述共享的约束节点的限制，得到了EMD的近似值，即近似环 EMD（Approximate Cycle EMD，ACE）。

当环中没有子环出现的时候，环中变量节点集的EMD与ACE是相等的，否则，ACE成为EMD的上限。为了简单起见，构造算法中的参数是ACE而不是EMD。度数低的变量节点的ACE值小。相对的，度数低的变量节点容易形成环，ACE值较小的环与图中其他节点的连接也较少，而连接较少的子图容易受到噪声的影响。ACE算法可以较好地解决这个问题，它的基本思想是:构造LDPC码时，保证所有环长小于一定值的环都有一定的ACE值[2]。

上述基于ACE的算法使得具有高连接性的短环被保留，但低连接性的长环被消除。采用这样的方法可有效降低不规则LDPC码的错误平底。将准循环码的限制加入到ACE算法中，可以获得准循环码的校验矩阵。

4 基于ACE的构造算法

结合上述基于ACE的算法，这里给出一种结构化LDPC码的构造方法。指数矩阵中非零节点数通过密度进化的方法获得。算法中逐次检验围长和节点的连接性，据此更新检验矩阵的循环值。根据前面的分析，构造过程总结如下:

1）根据码率和码长确定指数矩阵大小m，n和循环值p；

2）根据密度进化来生成指定码率的最优度分布，并根据矩阵大小对度分布修改，确定各指数矩阵中的非零元素的分布；

3）确定指数矩阵中的非零元素取值，将对应的信息节点逐次与所有校验节点相连，并比较[0，p-1]内所有循环值，根据相应的环长和连接性，ACE选择最优的连接和循环值；

4）将步骤3）的循环值加入指数矩阵，重复步骤4），直至指数矩阵所有非零元的循环值被确定。

本算法中对每个非零元采用迭代赋值算法，通过最大化局部围长和ACE，减少了小的陷阱集。算法中逐步检查每个比特节点并按照下述条件更新循环值。根据当前循环移位值检查环长和连接性，将其和前一个循环移位值的对应环长和连接性比较。如果条件满足，则将循环移位值更新为当前值。第一个条件是当前环长大于此前的环长，第二个条件是当前连接性不低于此前连接性。

指数矩阵各元素的取值为位于该位置的块矩阵的循环移位值，其取值范围为[0，p-1]。根据密度进化计算得到最优度分布，计算得到各信息节点连接的校验节点个数，然后逐次将信息节点连接到校验节点，通过最大化环长和连接性的方法，选择能够保证环长和连接性最大化的校验节点连接。对于指定节点度分布的Tanner图，逐次将每个变量节点连接到不同的校验节点，在建立连接的过程中，将[0，p-1]内所有可能的循环值逐次加入到指数矩阵的当前位置。对每个循环值，计算出相应的环长和环的外在连接性ACE值，若当前循环值对应的环长和ACE值均大于此前计算循环值的对应值，则将循环值更新为当前循环值，否则保留原循环值；若当前环长小于此前的环长，则保留原循环值；若当前环长等于此前环长，则比较两个循环值对应的局部环长和，取局部环长和较大的循环值。此处局部环长和为经过指数矩阵中已经赋值部分的各元素所形成的环长总和。

算法通过信息节点对应的校验节点和非零元素循环值的遍历，保证了指数矩阵在可能的范围内能够取最大化环长和连接性。经过若干次的替换过程以后，各个元素对应的循环移位值都使得通过对应节点形成的环长最长且连接性最大，此时得到最终的指数矩阵。该算法可使得每个循环偏移在当前指数矩阵中形成最大的环长和连接性ACE，减少了停止集对码性能的影响；在最大化环长和连接性的条件下，同时尽量保证获得最大局部环长，从而保证码的整体环长性能。本算法对每个元素考虑了各种循环值，但是算法的复杂度并不高，因为算法中是对循环移位矩阵的指数矩阵来进行赋值处理的。综上分析，本算法所构造的码具有较好的纠错性能。

5 仿真与分析

对所提算法进行仿真，采用了BPSK调制，通过加性高斯白噪声信道传输，采用置信传播算法进行译码，最大迭代次数为 100。选取了（576，288）与（1056，528）两种码，根据同样的度分布用PEG算法和ACE算法生成两组码，编码码率均为1/2，对误码性能进行了对比，结果见图1和图2。

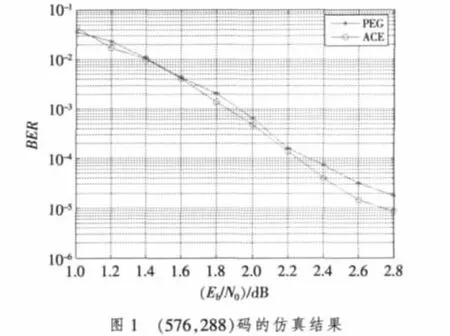
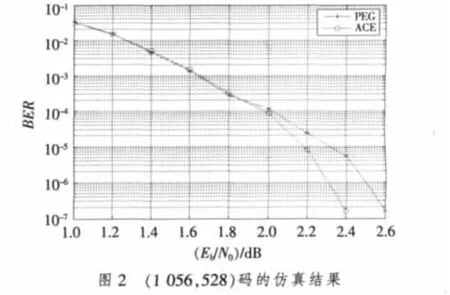
图1中，码长为576的仿真中显著地降低了误码平台，图2中码长为1056的仿真中瀑布区域的误码下降更陡峭。由图可见，根据基于ACE的算法设计的QCLDPC码在高信噪比时表现出更好的误码性能。

6 结论

笔者通过码型结构和译码实现的分析确定了构造准循环LDPC码，通过分析LDPC码的性能限制因素，给出基于外信息度的LDPC码构造算法。该算法采用基于ACE的方法来构造准循环LDPC码的指数矩阵，通过最大化环长和连接性ACE，减少了陷阱集对码性能的影响；在最大化环长和连接性的条件下，尽量保证获得最大局部环长，从而保证码的整体环长性能。

笔者所提出的QC－LDPC码构造方法，不仅能够构造具有较大最小停止集的QC－LDPC码，而且设计灵活，适用于正则和非正则QC－LDPC码的构造，是一种有效的构造方法。仿真分析也验证了此方法的有效性。

[1]TIAN T，JOHNS C，VILLASENOR J D，et al.Selective avoidance of cycles in irregular LDPC code construction[J].IEEE Trans.Commun.，2004，52（8）:1242－1248.

[2]SHANNON C E.The mathematicaltheory ofcommunication[M].Urbana，IL:University of Illinois Press，1998.

[3]VUKOBRATOVIC D，SENK V.Evaluation and design of irregular LDPC codes using ACE spectrum[J].IEEE Trans.Commun.，2009，57（8）:2272－2279.

[4]KANG Jingyu，FAN Pingyi，CAO Zhigang.An iterative scheme of stopping set enlargement in the design of short－length irregular LDPC codes[C]//Proc. 3rd International Conference: Science of Electronic，Technologies of Information and Telecommunications.Susa，Tunisia:[s.n.]，2005[2009－11－01].http://www.setit.rnu.tn/last_edition/setit2005/reseau/217.pdf.

[5]朱慧琳，宋健，彭克武.基于代数构造和矩阵变换的准循环LDPC码组设计[J].电视技术，2009，33（S2）:36－39.

[6]HE Huan，XU Youyun，CAI Yueming.Irregular quasi－cyclic LDPC codesdesign with generalized ACEconstraint[C]//Proc.2009 International Conference on Communications and Mobile Computing. Kunming，China:[s.n.]，2009:196－199.