GDH512电主轴振动特性分析

伍良生 周 亮 肖毅川

(北京工业大学机械工程及应用电子技术学院，北京100124)

高速电主轴作为高速机床的核心部件日益向高速度、高刚度的方向发展，要使高速机床安全可靠地工作，保证所加工零件的高精度，高速电主轴必须具有良好的动态特性。因此，必须对它进行动力学研究。有限元动力学分析是一种先进的新方法，具有其他方法无法比拟的优点，如节省投资、缩短产品开发周期等。高速电主轴的有限元动力学分析包括两个方面，固有振动特性分析和谐响应特性分析。

本文是通过分析无阻尼的自由振动，得到振动系统的固有特性，即固有频率和振型及振动应力。而谐响应特性分析是用于确定结构在承受随时间按正弦规律变化的载荷的稳定响应，目的是计算出结构的动力学响应，并得到响应位移和响应应力。

下面以GDH512高速电主轴为例，进行相关的有限元动力学分析。

1 主轴部件的动力学模型

1.1主轴部件的结构特点

为了对电主轴进行相关的动态特性分析，有必要先了解清楚GDH512高速电主轴的结构特点，以便在分析过程中，构建合理的有限元分析模型。如图1所示是GDH512高速加工用的电主轴三维图。其中，前支撑是3套角接触球轴承背对背配置，后支撑是双列圆柱滚子轴承。为了保证加工的精度和稳定性，前轴承是固定的，承受径向载荷和双向轴向载荷;为了补偿加工中轴向热变形，后轴承在轴向可以有微量位移。前后轴承均采用定位式预紧。电动机转子用压配合方法安装在主轴上，处于前后轴承之间。电动机定子通过冷却套安装在电主轴的壳体中。主轴内部安装OTT公司生产的HSK拉刀机构。主轴后部安装有测速传感器。主轴轴承采用油-气润滑系统进行冷却和润滑。电动机采用油-水热交换系统进行冷却。

1.2 主轴弹性支承模型的构建

将每组轴承简化为四个周向均布的压缩弹簧，见图2。

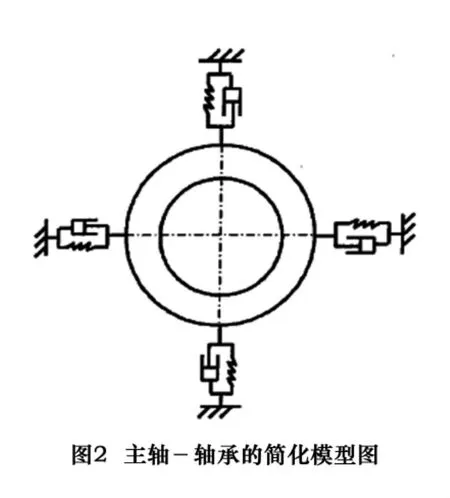
每个弹簧都用一个弹簧-阻尼单元Combin14来模拟。弹簧单元Combin 14可应用于一维、二维或者三维空间在纵向或者扭转的弹性-阻尼效果。如图3所示，x、y、z表示单元坐标，I，J表示单元的两个节点，k表示弹簧刚度，Cv表示弹簧阻尼。因此，这两个参数就是该弹簧单元的输入参数。

为了限制主轴的轴向移动，在与弹簧相联接的4个主轴上的节点加上轴向约束，在弹簧的另外一端为完全固接，每个弹簧的刚度为相应轴承径向刚度的一半。由于主轴是由四个角接触的陶瓷球轴承来支承，所以要考虑轴承的弹性对主轴固有振动特性的影响［1］。因此，有必要将轴承的弹性影响引入到支承的两个轴承上。并作以下假设:

(1)外圈固定，内圈在负荷的作用下产生位移;且滚动体的陀螺力矩作用在滚动轴线上，不影响接触变形。

(2)内外圈分别安装在高刚性的轴和轴承座上，忽略套圈的弯曲变形，在变形协调条件中仅考虑接触处的弹性变形。

(3)忽略轴承内的摩擦。因为与套圈作用在滚动体上的负荷相比，摩擦力很小。

已知轴向预紧力为Fa的前提下，后轴承预紧后的径向刚度Kr按如下公式进行计算［2］:

前轴承刚度

式中:Kr为轴承径向刚度，N/m;z为滚动体数目;DW为滚动体直径，mm;接触角，(°);Fa为轴向预紧力，N;km为材料系数，取km=1.3。

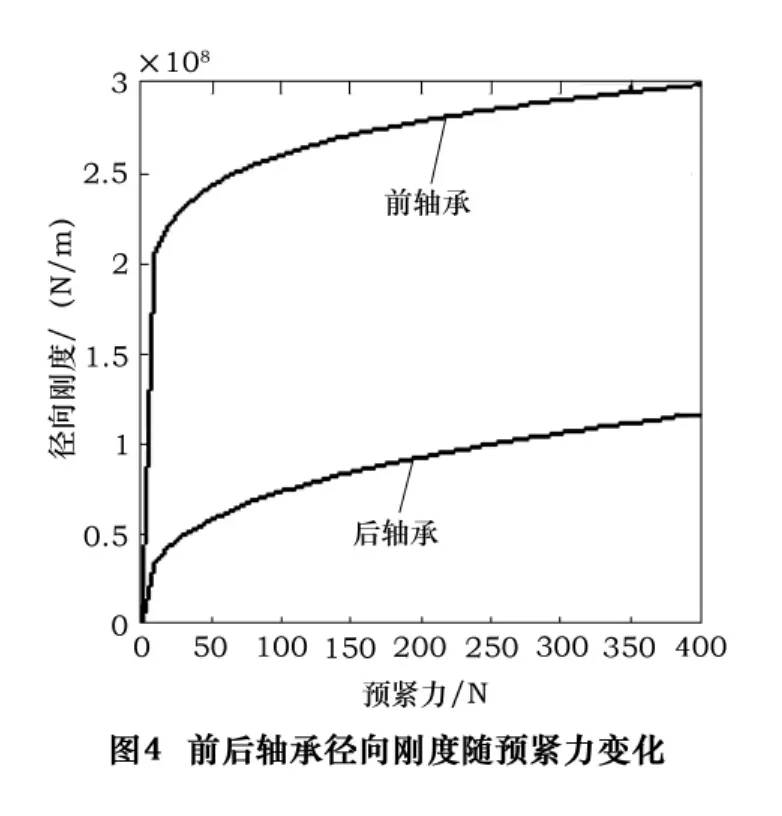
由于角接触球轴承径向刚度在承受轴向载荷时表现的非线性，针对施加不同轴向预紧力的情况作了若干组关于静态刚度的分析，结果如图4所示。

1.3 主轴三维模型的理论构建

根据电主轴的结构特点，在ANSYS分析平台中，对电主轴选用SOLID45单元进行离散分网。此单元是分析弹性结构空间问题中应用较广的一种元素。由于采用了八节点的单元，那就能利用更复杂的形状函数，并因而达到结构对实际变形的一个更高程度的表达，计算精度较高。而且，SOLID45单元是三维8节点等参单元。所谓三维8节点等参单元是指8个节点的六面体的等参基本单元，如图5所示。并且，它映射成8节点的等参实际单元。

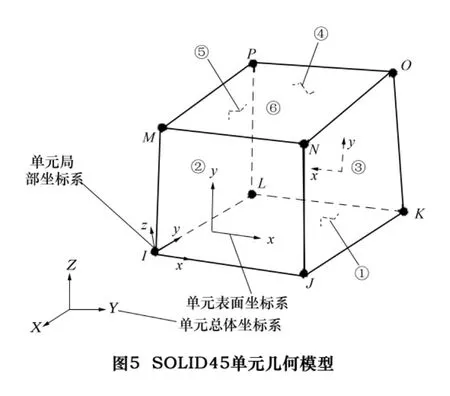
数控铣床主轴材料采用20CrMnTi钢，材料弹性模E=210 GPa，密度 ρ=7820 kg/m3，泊松比 μ =0.3。采用SOLID45单元，轴承用COMBIN14单元来模拟。划分网格过程中，由于是轴对称，所以先在轴的剖面图上细化网格，然后用Extrude延伸生成三维网格。这样使得网格划分有规律，而且单元数量少，分析准确。由以上分析忽略轴承的轴向刚度在ANSYS中建立有限元模型如图6。

1.4 模态分析

研究机床主轴部件的动态性能，首先要建立系统的动力学微分方程。多自由度的动力学微分方程可以应用牛顿第二定律等来建立。根据达朗伯原理，只要引入相应的惯性力，就可以将弹性体转化为相应的静力问题，即转化为弹性体的平衡问题来求解。即有［3］:

式中:［M］为总质量矩阵;［MT］为平动自由度质量矩阵;［MR］为转动自由度质量矩阵;［K］为刚度矩阵;［KS］为轴体刚度矩阵;［Kb］为轴承刚度矩阵;［C］为阻尼矩阵;［J］为回转矩阵;{x(t)}为节点位移列向量;{F(t)}为激振力向量。

上式是研究电主轴动态特性的一般公式。可以看出，影响主轴动力学特性的因素有阻尼效应［C］、陀螺效应、离心力效应以及载荷的性质。

模态分析是指通过研究无阻尼系统的自由振动，得到振动系统的自然属性，即固有频率和振型。阻尼的存在，使电主轴在振动的过程中振幅不断衰减，并产生一个滞后的幅角，然而它对固有频率的影响不大。对于支撑为滚动球轴承的时候，可以忽略阻尼对固有频率的影响。无阻尼系统的振动方程为

由式(3)得:

其中:{A}为系统振幅矩阵;ω0为系统固有频率。

如{A}有非零解，则有:

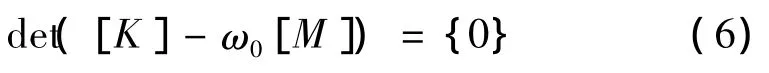
求解式(6)的广义特征值和特征向量，即可得到主轴部件的固有频率和振型。

对电主轴进行模态分析的任务是确定其固有频率和相应的振型。有限元软件 ANSYS提供了 Block Lanczos法、子空间法、PowerDynamics法、缩减法、不对称法、阻尼法和QR阻尼法。使用何种模态提取方法主要取决于模型大小和具体的应用场合。本文不考虑电主轴的高速效应和轴承刚度的非线性，使用Block Lanczos法进行固有频率的提取。计算出主轴的前四阶固有频率和振型如表1和图7。

1.5 轴承预紧力对主轴固有频率的影响

根据文献［4］可知道，随着预紧力的增加，前后轴承的径向刚度均有不同程度的增大。首先，取后轴承预紧力为200 N不变，改变前轴承的预紧力，观察主轴固有频率的变化。因此，如图8所示的，是主轴一阶固有频率随前轴承预紧力的变化而变化的情况。

表1 电主轴固有频率

再取前轴承预紧力为300 N不变，改变后轴承的预紧力，观察主轴固有频率的变化。因此，如图8所示的，是主轴一阶固有频率随后轴承预紧力的变化而变化的情况。

2 高速电主轴的谐响应特性分析

谐响应分析必须在完成模态分析之后进行。因此，利用ANSYS分析软件进行谐响应分析。建模过程与之前介绍的模态分析的是一样的。而激振力的大小采用的径向力F=300 N，加载在主轴的前端上部。

为了分析共振区首先研究一阶固有振动频率183 Hz附近的响应特性。取激振力的频率范围为100～220 Hz，载荷子步为20，得出主轴中部点响应位移对频率的曲线图，如图9所示。

当激振力的频率从160 Hz增加到185 Hz时，主轴中部的径向响应位移急剧增加，主轴的动刚度显著下降;当激振力的频率再增加到220 Hz左右时，主轴前端的径向响应位移急剧下降，主轴的动刚度回升;另外，在160 Hz频率以下主轴前端的动态位移量都很小，表明主轴在这频率段具有良好的动刚度。

由此可进一步确定，共振区出现在频率为185 Hz附近，即一阶固有频率附近。而本文所介绍的GDH 512高速电主轴的最高工作转速为5000 r/min，也就是工作频率最高为83 Hz，因此，能有效避开共振区。

3 电主轴动态特性试验

(1)主要试验装置 JZK-10激振器一个;YE5872A功率放大器一个(200 W);CL-YD-331阻抗头一个(力+加速度);YE5852B电荷放大器一个;数据采集系统;SKJZCP-1软件系统。

(2)试验条件及方法 在静态下，在主轴前端激振和拾振，主轴前端动刚度，由实测频响函数识别固有频率和阻尼比;由实测主轴前端动柔度曲线识别主轴前端静、动刚度。

实测电主轴轴(径)向前端动柔度曲线具体操作:①将电主轴调整至C轴模式;②将阻抗头紧固安装在电主轴前端轴心(径向将阻抗头垂直轴心线紧固安装)，然后用激振杆将激振器与阻抗头紧固连接(如图10所示);③连接激振器与功率放大器;④将阻抗头的力和加速度信号分别接入电荷放大器，调整电荷放大器增益;⑤将数据采集系统输出端AO0接至功率放大器，分别将电荷放大器输出的力和加速度信号接入数据采集系统;⑥打开SKJZCP-1软件系统，调整功放增益，开始激振实验，测试并显示存储处理结果。

(3)测试数据处理与记录 电主轴径向实测频响函数如图11所示。根据其实测频响函数曲线，峰值点可确定固有频率及动刚度，在峰值点附近由半功率带宽法可确定阻尼比，按实测频响函数的构成可分离出静刚度。结果如表2。

表2 动静态特性测量输出参数表

试验数据与ANSYS建模得出的数据相差不到5%，所以建模可行，可以用于进一步的计算研究。

4 结语

本文采用有限元分析方法，并运用ANSYS软件对GDH512高速电主轴进行了动态特性分析，结果表明:

(1)主轴的工作频率远远低于其固有频率。因此，工作转速不会达到临界转速，主轴可以安全工作。

(2)前后轴承的刚度对主轴的固有频率均有影响，其中，后轴承的影响较为显著。

(3)主轴的一阶固有振动频率是183 Hz，远远高于工作频率。因此，主轴在工作范围内不会发生共振现象。

(4)当工作频率达到 259 Hz，388 Hz，460 Hz 时，就会发生共振，而且主轴中部的振幅最大，是危险点，容易产生裂纹缺陷。

1 Jorgensen，Bert R.Dynamics of spindle-bearing systems at high speeds including cutting load effects.Journal ofmanufacturing science and engineering，Transactions of the ASME，1998，20(12):387-394

2 胡爱玲.高速电主轴动静态特性的有限元分析:［硕士学位论文］.广州:广东工业大学，2004:30～31

3 Chiwei Lin，Jay F.Tu，Joe Kamman.An Integrated Thermal-mechanical-dynamic Model to Characterize Motorized Machine Tool Spindles during veryHigh Speed Rotation.International Journal of Machine Tools ＆Manufacture，2003，43:1035-1050

4 蒋兴奇.主轴轴承热特性及对速度和动力学性能影响的研究:［博士学位论文］.杭州:浙江大学，2001:101～112

5 张柏霖，张志润，肖曙红.超高速加工与机床的零传动.中国机械工程，1996，7(5):37～41

6 RollerBearings Load in Five Degrees of Freedom While Neglecting Friction-Part I:General Theory and Application to Ball Bearings.Journal of Tribology，1989，111(1):142-148

7 李松生.高速精密角接触球轴承支承特性分析.轴承，2001(2):11～14