时速 140 km城市轨道交通简支梁桥竖向刚度限值研究

邓建良,李 奇,吴定俊

(同济大学桥梁工程系,上海 200092)

1 概述

欧洲和日本的研究表明,控制桥梁刚度(通常以挠跨比表示)的主要目的是为了满足车辆的乘坐舒适度要求。最新欧洲规范“EUROCODE”和 2006年日本铁道综合技术研究所编制的标准均依据乘坐舒适度要求确定了桥梁的挠度限值[1～2]。桥梁的挠度限值由桥梁跨度、车速和车辆类型这 3个因素决定,这一点在欧洲和日本规范中均得到体现。目前我国针对城市轨道交通高架结构的设计规范[3～4],所适用的最高设计车速为 100 km/h,这一车速已不能满足近年来一些轨道交通高架桥梁的设计要求。因此,必须在掌握国内外桥梁挠度限值制定的依据的基础上,针对新的工程设计荷载和设计车速的特点,重新制定桥梁跨挠比限值,以确保工程安全、乘车舒适,并为结构优化设计提供依据,实现较好的经济性。

2 车辆模型与车桥耦合振动分析方法

以定员载重情况下的地铁 A型机车为代表车辆,车辆看做由车体、转向架、轮对 3个部件组成,且每一部件均假设为刚体,各部件之间由弹簧及阻尼器连接。车体和转向架均考虑 5个自由度:即沉浮、点头、横摆、摇头及侧滚,轮对考虑2个自由度,分别为横摆及摇头。4轴客车车辆计算模型由 1个车体、2个转向架和 4个轮对组成,整车系统共有 23个自由度[5]。本文采用的计算原理是将车桥分成两个动力系统,分别建立动力平衡方程,假定轮轨竖向始终密贴接触,通过迭代计算实现轮对与轨道相互作用力和位移的协调,车桥振动微分方程的具体形成和数值求解过程可参见文献[6]。

3 舒适度评定标准

为制定桥梁跨挠比限值,必须首先确定评定乘坐舒适度等级的方法和标准。目前关于乘坐舒适度的评定方法众多,欧洲规范依据车体最大加速度确定乘坐舒适度等级,日本则主要采用 Janeway等舒适度评定方法,我国铁路车辆部门主要采用 Sperling指标。不同的舒适度评定方法各有优缺点,且具有一定的差异性。为使得研究更具有一般性和国际化,同时考虑到我国轨道交通桥梁设计的特点以及研究的实用性,本文将分别采用国际标准 ISO2631(《人体承受全身振动的评价指南》)与我国高速铁路设计规范[7]规定的乘坐舒适度指标为评定标准对桥梁跨挠比限值进行研究。

ISO2631—1:1997标准[8]建议了总乘坐值与人体舒适度的对应关系,如表1所示。

表1 总乘坐值与主观感受的关系

假定轨道不平顺产生的车体振动加速度与桥梁引起的车体加速度不相关,则统计分析表明,只要桥梁变形产生的车体加速度 RMS值[8]小于 0.315m/s2,则即使在轨道状况不良的情况下,乘坐舒适度也不会显著降低,能够达到“稍有不舒适”标准,而基本不会超过“比较不舒适”的程度。因此,当采用 ISO2631—1:1997标准时,本文将桥梁产生的车体加速度 RMS值限制在 0.315m/s2之内,据此制定桥梁跨挠比限值。

我国《高速铁路设计规范(试行)》(TB10621—2009)规定:旅客乘坐舒适度指标应满足车体竖向加速度(半峰值)小于等于 0.13g的要求。经统计分析发现,在不计轨道不平顺的影响时,当桥梁振动引起的车体竖向加速度(半峰值)不超过 0.10g时能满足规范规定的舒适度要求,本文即以此为标准来研究桥梁的竖向刚度限值。

4 计算成果分析

4.1 基于半波正弦模型的跨挠比限值

日本在制定桥梁跨挠比限值时主要依据半波正弦模型[9],即采用半波正弦曲线来模拟桥梁在列车静荷载下的变形(图1),并以此静态变形作为轨道不平顺对移动车辆进行激励。对于某一跨度的桥梁,改变其跨挠比(即改变半波正弦曲线的波幅),当车体振动加速度或者舒适度指标达到限值时对应的跨挠比即为跨挠比限值。

图1 5跨简支梁的半波正弦模型

图2为根据半波正弦模型确定的不同设计车速下各跨度桥梁跨挠比限值。不难发现,设计车速越高,为满足乘坐舒适度要求,所需要的桥梁跨挠比越大。当采用 ISO2631—1:1997标准的舒适度指标时,短跨度桥梁的跨挠比限值需更严格,当跨度超过某一值时,跨挠比可随着跨度增大而适当放松。当采用高速铁路设计规范的舒适度指标时,由图2(b)可知,在各设计车速下,桥梁的跨挠比限值随跨度的变化存在一个临界值:当跨度超过临界值时,跨挠比限值基本上不随跨度的变化而变化;当跨度小于临界值时,跨挠比限值随跨度的减小而减小且变化较大。也就是说,短跨度桥梁的跨挠比限值相比于较大跨度桥梁来说更加宽松。由此可见,两种不同的舒适度评价标准导致跨挠比限值截然不同。另外,容易从图2得知,对于跨度为 30 m桥梁,当设计车速V=140 km/h时,其跨挠比限值约为1 500,而在设计车速为 100 km/h的情况下,其跨挠比限值约为1 000(RMS指标)、1 200(半峰值指标)。《地铁设计规范》(GB 50157—2003)中规定的这一跨度的跨挠比限值为2 000,初步表明其相对于设计车速100 km/h而言是比较保守的。

图2 不同车速下各跨度桥梁跨挠比限值

半波正弦模型能较好地模拟桥梁变形导致的不平顺对车辆的激励作用,且概念明确,计算简单,其缺点是不能反映车桥之间的耦合作用,不能反映桥梁在其动力平衡位置的上下振动,可能低估桥梁变形和振动对车体振动的影响。本文采用 5跨简支梁的半波正弦模型初步确定桥梁跨挠比限值,然后用更为精确的考虑车桥动力耦合的计算模型确定最终的跨挠比限值。

4.2 基于动力耦合模型的跨挠比限值

车桥耦合动力计算中,桥梁的刚度、质量以及阻尼均须合理确定。以某 30m跨度高架桥简支梁 U形截面为原型,通过改变截面高度和板厚的方式来获取不同截面惯性矩和截面面积的匹配值,由此得到 10～100m跨度桥梁不同刚度和自重的可能范围。桥面二期恒载不随桥梁跨度和桥梁刚度的变化而变化,均取为 37 kN/m。桥梁阻尼采用瑞利阻尼[10]的方式处理,0.5Hz和 30Hz频率对应的阻尼比均取为 0.02。

采用 8节编组列车通过 5跨简支梁进行耦合振动分析。计算车速为 96～168 km/h,速度间隔为 6 km/h,考虑到理论计算与实际情况的差别,参考欧洲规范的做法,将计算车速比设计车速提高 20%。由于车桥动力耦合模型具有非线性,因此舒适度指标达到相应要求时所对应的桥梁跨挠比须经过多次试算确定。

图3为采用动力耦合模型时,针对不同跨度、不同跨挠比的桥梁的车体加速度 RMS指标、半峰值指标计算结果。图中各个离散点旁边的数值表示对应的桥梁跨挠比,括号中的数值为相应竖向自振基频。从图中可见,对某一跨度的桥梁,跨挠比越大,桥梁刚度越大,桥梁变形和振动越小,车体加速度 RMS指标与半峰值指标也越小。当车体加速度接近但不超过 0.315m/s2(RMS指标)、0.10g(半峰值指标)时所对应的桥梁跨挠比可作为相应跨度跨挠比的限值,即图中加粗的跨挠比。

根据图3可获得基于动力耦合模型得到的 10～100m跨度桥梁的跨挠比限值,并将根据半波正弦模型得到的跨挠比限值对比,如图4所示。可见,对于10～40m跨度的桥梁,采用动力耦合模型计算的跨挠比限值比采用半波正弦模型计算的跨挠比限值要大,这是由于这类跨度的桥梁,动力耦合作用比较显著,因半波正弦模型不能考虑桥梁的振动,从而低估了桥梁对车体振动加速度的影响。但是当桥梁跨度大于 50 m时,车桥耦合作用减弱,且因定员车辆自重略轻于实际设计荷载,使得动力耦合模型下桥梁的实际挠度小于设计挠度(半波正弦曲线的幅值),导致采用半波正弦模型计算的跨挠比限值是偏于安全的。动力耦合模型的分析结果再一次表明,采用不同的舒适度评价标准得到的跨挠比限值有较大的差别。

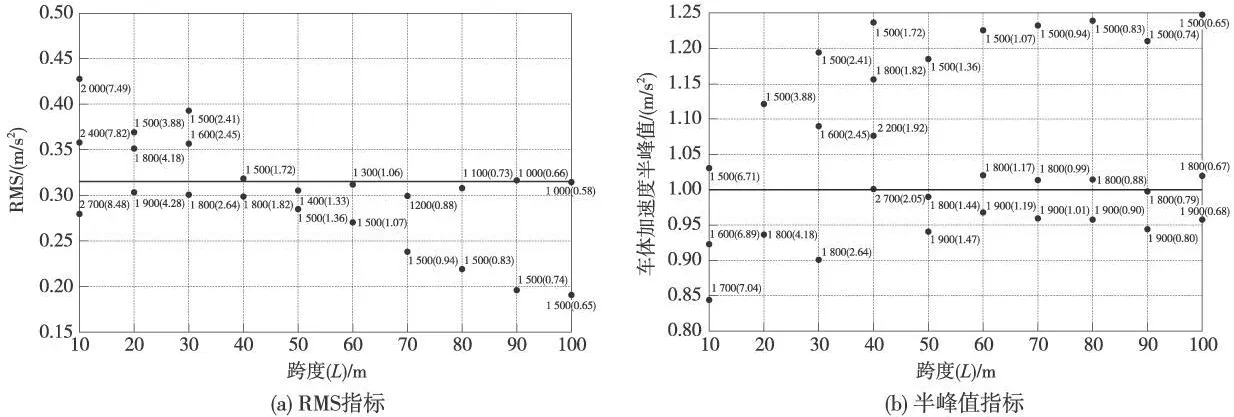
图3 根据动力耦合模型计算的不同跨挠比下车体加速度指标值

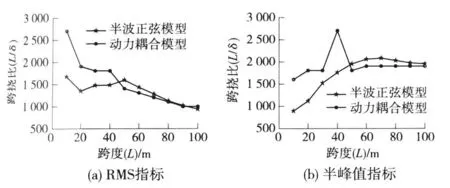
图4 半波正弦模型与动力耦合模型分析得到的跨挠比限值

分别采用半波正弦模型和动力耦合模型对桥梁跨挠比限值进行分析,两者相互校核、验证,表明了分析结果具有较高的可靠性。鉴于车桥动力耦合模型的合理性,建议采用动力耦合模型得到的跨挠比限值作为设计参考。

5 行车安全性、桥梁安全性与轨道稳定性检验

以上跨挠比的建议限值是仅以满足乘坐舒适度要求而制定的,还需通过车桥动力耦合分析检验行车安全性、桥梁结构的安全性以及轨道结构的稳定性是否满足要求。表2、表3为采用动力耦合模型计算的不同跨度桥梁刚度达到跨挠比限值时对应的最大轮重减载率、桥梁跨中弯矩冲击系数与桥梁跨中竖向最大加速度。

对于竖向振动而言,行车安全性一般以轮重减载率来衡量。我国国家标准[11]规定的车辆轮重减载率容许限度为 0.60。从表2、表3中可见,桥梁变形和振动引起的最大轮重减载率不超过 0.25,考虑轨道不平顺等级为 6级后最大轮重减载率不超过 0.3,在轨道不平顺等级为 5级时最大轮重减载率也不超过 0.6的容许限度。因此,根据 RMS指标与半峰值指标制定的最小跨挠比均能满足行车安全性要求。

表2 行车安全性、桥梁安全性与轨道稳定性检验(RMS指标)

为确保桥梁结构安全使用并具有较好的耐久性,应避免发生显著的车桥共振现象。是否发生车桥共振可以用桥梁位移或者内力动力系数来判断。由表2、表3可见,对于跨度为 10～50m的桥梁,桥梁跨中位移动力系数较大,尤其是 40、50m桥梁,其动力系数达到 1.4～2.0,远远超过设计动力系数,分析表明,这是由于这一跨度范围的桥梁自振频率与车辆激振频率相吻合而发生了共振。也就是说,满足乘坐舒适度要求的桥梁不一定能避免车桥共振,也不一定能确保桥梁的安全性与耐久性。为解决这一问题,除对桥梁跨挠比进行限制,还应对桥梁自振频率进行限制。

欧洲规范“EUROCODE”规定,为保证轨道稳定性,对于有道砟的桥梁,桥梁竖向加速度不得大于 3.5 m/s2,而对其他无砟桥梁,桥梁竖向加速度不得大于5.0m/s2。计算桥梁加速度时至少考虑结构的 3阶振型,且频率考虑至 max[30,λf0],f0是结构的 1阶自振频率,λ=1～2。城市轨道交通一般采用无砟轨道,为保证轨道稳定性,在上述频率范围内的桥梁跨中竖向加速度不得大于 5.0m/s2。从表2、表3可见,各跨度桥梁跨中加速度均小于 5.0m/s2。应该注意到,跨度越小,桥梁加速度越大,且越接近限值,因此对于小跨度桥梁,在满足乘坐舒适度的前提下,可进一步提高跨挠比限值,以增强轨道结构的稳定性。

6 结论

通过本文的分析,可以得出如下初步结论。

(1)分别采用 ISO2631—1:1997标准的 RMS指标和我国高速铁路设计规范的半峰值指标为舒适度评价标准,初步制定了 10～100m跨度桥梁跨挠比限值,并根据行车安全性、桥梁安全性和轨道稳定性检验,提出适合地铁 A型车辆设计车速 140 km/h的桥梁跨挠比限值如表4、表5所示。

表4 桥梁跨挠比限值(RMS指标)

表5 桥梁跨挠比限值(半峰值指标)

表4、表5适用于两跨及以上的单线简支梁,对单跨简支梁,可对相应的跨挠比限值乘以 0.7的系数。若结构在长期收缩、徐变作用下产生下挠或者在日温差作用下梁体发生下挠,则有必要将这些下挠值与列车活载作用下挠值进行组合,再根据表4、表5检算桥梁跨挠比。对于在设计阶段采用预拱度抵消梁体设计挠度的场合,可以将表中跨挠比限值适当放宽。

(2)设计车速 140 km/h的车辆的激振频率在 2 Hz附近,与 40～50m跨度的简支梁自振频率接近,可能引起共振现象,为保证桥梁安全性,除采用跨挠比限制外,还须对桥梁自振频率进行合理限制。

[1] UIC Code 776—3,Deflection of Bridges[S].

[2] 日本铁道综合技术研究所.铁道构造物等设计标准同解说——变位限制[S].

[3] GB 50157—2003,地铁设计规范[S].

[4] DGJ 08— 109—2004,城市轨道交通设计规范[S].

[5] 王福天.车辆动力学[M].北京:中国铁道出版社,1991.

[6] 吴定俊.提速线上桥梁振动理论与横向动力性能的研究[D].上海:同济大学桥梁工程系,2005.

[7] TB10621— 2009,高速铁路设计规范(试行)[S].

[8] ISO2631— 1:Mechanical vibration and shock— Evaluation of human exposure to whole-body vibration—Part 1:General requirements[S].1997.

[9] Sogabe M,Furukawa A,Shimomura T,et al.Deflection Lim its of Structures for Train Speed-Up[J].Quarterly Report of RTRI,2005,46(2):130-136.

[10] Clough R W,Penzein J.Dynam ics of Structures[M].McGraw.Hill Inc,1993.

[11] GB 5599—85,铁道车辆动力学性能评定和试验鉴定规范[S].