对角变换四染色平面图
徐秋茹,赵寒涛,李乃川,黄兴滨
(1.黑龙江省科学院自动化研究所,黑龙江哈尔滨150090;2.黑龙江大学物理科学与技术学院,黑龙江哈尔滨150080)
四色猜想源于英国的F.Guthrie提出的:使用四种颜色就能够给所有地图染色而使两个有公共线段边界的区域染以不同的颜色。所有地图意味着不仅仅是世界地图集上的全部地图,而是可以想象得出的所有地图,地图也许会有成千上万(或更多)的国家、各种可能的形状、大小和彼邻关系。由于其证明的难度使其成为继Fermat大定理之后又一著名的数学未解问题。1976年,两位美国数学家,Appel和Haken宣称他们证明了四色问题。但有不尽人意之处。因为他们的证明主要由计算机完成,并且证明程序太长,人工无法检查其正确性[1]。
尽管已经证明了四色猜想,但如何给任意一个平面图进行四染色还没有解决,还停留在试验染色的阶段[2]。民航空域频率覆盖是典型的四染色问题案例。研究四染色问题对民航信息化建设有重要意义[3]。我们利用极大平面图的对角变换的方法尝试解决平面图的四染色问题。
1 对偶图与极大平面图
给地图染色问题与其区域的具体形状无关,仅与它们彼邻关系有关。所以四色问题是一个拓扑学问题。它很容易被等价为给平面图顶点染色的问题。
把给定地图的每个区域等价为一个点,通常叫做图的顶点。然后用边连接这些顶点形成一个图,规则是:只有也只有当两个顶点各自代表的地图区域有公共的边界线时才可以连接这两个顶点。按如此方法得到的图称为地图的对偶图。这样可以把地图的区域染色转换为其对偶图的顶点染色。而保证:该对偶图的顶点可以最多使用四种颜色染色而让有一个边连接的两个顶点具有不同的颜色。平面图就是可以在平面上画出且任何两边不会在端点之外相交的图。地图是一个平面图,所以其对偶图也是一个平面图,并且是一个简单平面图。
一种简单的平面图被定义为极大平面图:如果它是平面图,若增加任何一条边都将破坏其平面性。极大平面图的所有面都是由三个边组成,极大平面图也称之为三角抛分图。所以只要解决所有的极大平面图的四染色问题则解决了所有的平面图染色[4]。
2 标准图与对角变换
让我们选取最大平面图的一种特殊构型,如图1所示。我们称之为标准图。标准图的最小顶点数为4,标准图顶点数量的改变只能在顶点4到顶点n之间进行。明显的结论是:任意顶点数的标准图都容易用四色染色。
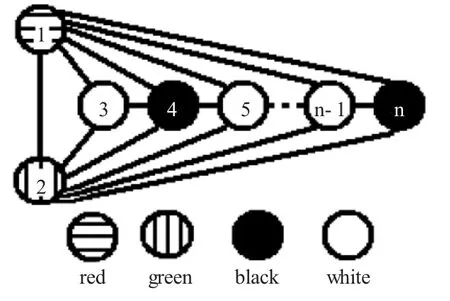
图1 具有n个顶点的标准图。按规则容易用红色、绿色、黑色和白色染它所有顶点。Fig.1 Standard drawing with n vertices.Color all the vertices with red,green,black and white regularly.
对角变换:在任意极大平面图中构成四边形的四个顶点中去掉连接对角顶点的边后,放一个新的边连接另一对顶点。图2给出了一次具体的对角变换,即去掉连接顶点②与④的边之后,放置一个连接顶点③与⑤的边。
对角变换给出了任意极大平面图与相同顶点的标准图之间的关系。可以证明逐次使用对角变换可以把任意极大平面图转化到它的标准图[5]。由于对角变换是可逆变换,所以也可以证明:从一个任意顶点的标准图出发,通过对角变换可以获得所有的极大平面图。

图2 用一次对角变换能把图1所示的标准图变成一个新的极大平面图。Fig.2 A new large planar graph by diagonal transformation changed from fig.1
3 对角变换的四染色方法
首先,将待染的极大平面图通过对角变换转换为标准图并记录好每一次对角变换的过程和次序。目的是容易找到从标准图到待染图之间的对角变换的关系。具体操作时要先把带染色的图抻成标准图的形状,并使各顶点保持原有的连接关系。这样就会很容易找到对角变换的次序。
其次,把上述的对角变换的次序和过程倒过来把一个同顶点的标准图通过对角变换转化为待染的极大平面图。目的是检查从标准图到待染图之间的对角变换的关系的正确性。
最后,先把标准图用四色染好,如图1;然后开始第一次对角变换,如图2所示。当新放置的边要连接的两个点颜色不同时则直接连接;若颜色相同则利用肯普网进行局部交换颜色至两顶点的颜色不同,这样保证在对角变换后的极大平面图还是四染色的;交换颜色的方法是把连接这两个顶点的肯普链的种类减少到两种即可。下一步重复上述过程进行第二次对角变换,又会得到一个四染色的极大平面图;重复直至完成全部的对角变换。则完成该图的四染色方案。
我们使用上述的染色方法成功地对著名的加德纳图进行了四染色处理。加德纳图是一个具有110个顶点的极大平面图,曾经被误认为是四色猜想的反例。换言之,染加德纳图需要五种颜色。可见使用四种颜色为其染色是相当困难的。但从110个顶点的标准图出发经过205次对角变换则可以获得加德纳图。因此成功得到了加德纳图的四染色方案。由于篇幅的限制我们在此略去染色的步骤。
4 结论
虽然借助计算机已经给出了四色定理的证明。但对任意的一个地图如何进行四染色还没有一个行之有效的方法,还局限在盲目的试验染色阶段。用我们介绍的方法成功地为加德纳图进行了四染色处理。因此利用对角变换给一个平面图进行四着色也许是一个有效的办法。只是所需的变换次数比较多,需要的中间图也较多。手工绘图比较繁琐。如果通过计算机编程处理全部的染色过程,则会较方便地解决平面图的四染色问题。这会给四色定理的应用带来无穷的魅力。
[1]K.Appel,and W.Haken.The solution ofthe four-color-map problem.Scientific American[J].1977,27(4):108~121.
[2]许寿椿.四色问题漫谈[J].科学中国人,1998,(4):41~44.
[3]王锦彪,王玮玮,郑芸,等.四色问题反例研究与民航空域频率覆盖[J].计算机工程,2005,31(7):1~2.
[4]王绍文.极大平面图结构研究[J].光子学报,1998,(2):167~172.
[5]刘彦佩.平面图的理论与四色问题(Ⅰ)[J].数学研究与评论,1983,3(3):123~136.

