偏斜工况下向心关节轴承应力场分析

魏立保，牛荣军，杨海生，邓四二

(1.中国直升机设计研究所，江西 景德镇 333001；2.河南科技大学，河南 洛阳 471003)

应用于航空领域的自润滑关节轴承，其稳定性、可靠性和使用寿命直接影响到主机的性能。对关节轴承进行性能分析首先要获得其应力场分布，而关节轴承内、外圈间为球面接触，到目前为止，利用解析方法求解其应力仍有一定困难，常采用平均应力计算，这与实际情况有较大误差。然而，随着计算机数值模拟技术和有限元方法的发展，国内、外逐步展开利用非线性有限元法对关节轴承进行力学和摩擦学性能研究。文献[1]利用ABAQUS商业软件对自润滑关节轴承的配合关系进行分析，给出不同配合关系下的内、外圈变形曲线。文献[2]采用ANSYS分析计算大型推力关节轴承在轴向、径向和联合载荷下的应力分布和压力与变形关系，基于分析结果对关节轴承的配合结构进行优化设计；文献[3]采用ABAQUS对向心关节轴承在极限径向载荷工况下的三维应力场进行计算；文献[4]利用ANSYS对向心关节轴承的球径结构进行优化选择以改善磨损性能；文献[5]应用ANSYS对复合材料端面轴承在不同载荷、转速和表层材料厚度工况下的温度场进行模拟分析。利用现代数值模拟技术可以方便地求解出关节轴承在各种结构参数和工况下的应力分布、温升变化等性能参数，可以直观分析关节轴承的危险部位，从而判断轴承材料是否发生破坏及其具体位置。通过关节轴承性能数值模拟分析不仅可以将产品的安全隐患消除在设计阶段，而且可以缩短产品的设计周期，能够在保证设计要求的前提下提高产品的设计水平。

下面采用有限元软件ANSYS对向心关节轴承在内、外圈相对偏斜工况下进行应力场分析，考察不同偏斜角下关节轴承内、外圈间的应力场分布和最大应力位置。

1 三维结构模型

由于向心自润滑关节轴承主要承受径向载荷，根据其结构的对称性，取一半进行有限元建模分析，可减少计算工作量，节约计算时间。 分析时心轴两端固定，轴承座上端面为加载面。其配合关系如图1所示。为了提高分析准确度，采用ANSYS有限元软件的Solid92单元对上述三维模型进行网格划分，内圈内径表面、内圈配合面和外圈外径表面采用Conta174单元，心轴外表面、外圈配合面和轴承座外表面采用Targe170单元，从而建立三个接触对。径向极限静载荷以面载荷形式施加在轴承座上端面。

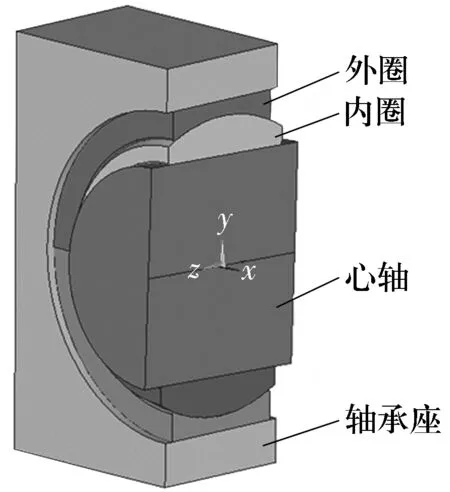
图1 装配结构示意图

2 径向极限静载荷下应力场分析

根据文献[1,3]，为了简化模型和减少计算时间，一般将心轴和轴承座视为刚性体进行分析，这与实际工况不符。为了说明不同心轴和轴承座材料属性对关节轴承应力场分布的影响，采用上述结构模型对心轴和轴承座分别设为刚性体和柔性体进行比较分析，其应力场分布如图2所示。

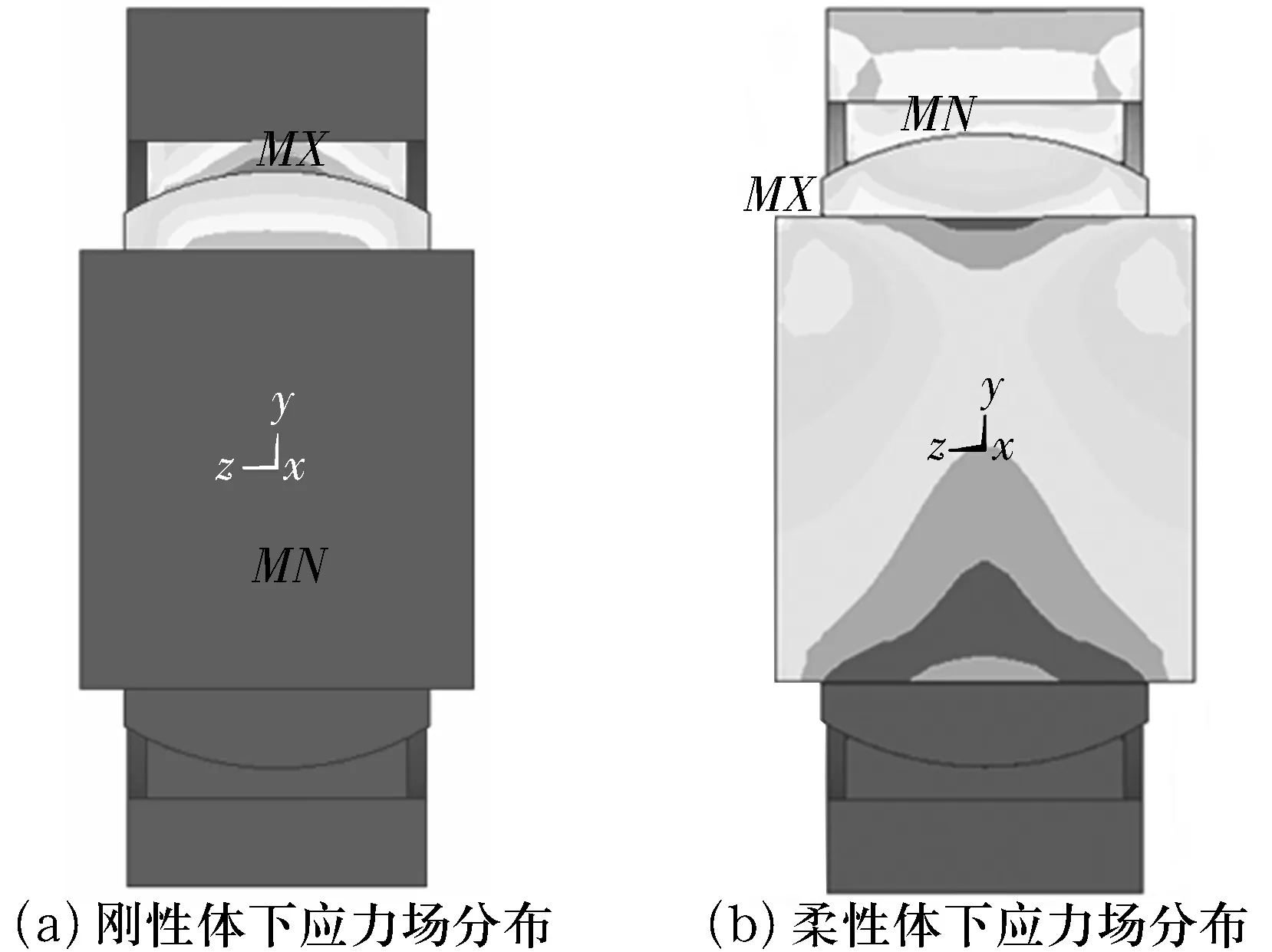
图2 不同心轴和轴承座材料属性下关节轴承的应力场分布

由应力分布结果可以看出，若将心轴和轴承座视为刚性体，最大应力位于关节轴承外圈接触面的中间位置，然后向两端逐步减小，比较符合余弦应力场分布的理论；将心轴和轴承座作为柔性体，这时要考虑心轴和轴承座的弹性变形，可以看到由于心轴两端固定使内圈的变形在靠近心轴两端处区域受到限制而产生较高应力，中间位置则应力值较小。由于内圈应力场分布的变化使得外圈的应力场分布受到影响，可以看到应力沿着外圈接触面分布较均匀，明显不同于余弦分布的理论假设。为了更真实地模拟实际工况，应将心轴和轴承座均视为柔性体进行分析。

3 偏斜工况下应力场分析

通常向心关节轴承在径向载荷下绕着轴线进行摆动，但对于一些特殊工况，向心关节轴承内、外圈间可能发生偏斜。在极限静载荷工况下，内、外圈相对偏斜将对关节轴承的应力场分布产生影响。为避免有限元模型分析中产生应力集中，分析中添加关节轴承内、外圈端面倒角，考虑过渡角后的结构模型如图3所示。所分析的关节轴承主要结构参数为：内圈尺寸Φ50 mm×35 mm(内径×宽度)，外圈尺寸Φ75 mm×30 mm(外径×宽度)，关节轴承材料参数见表1。

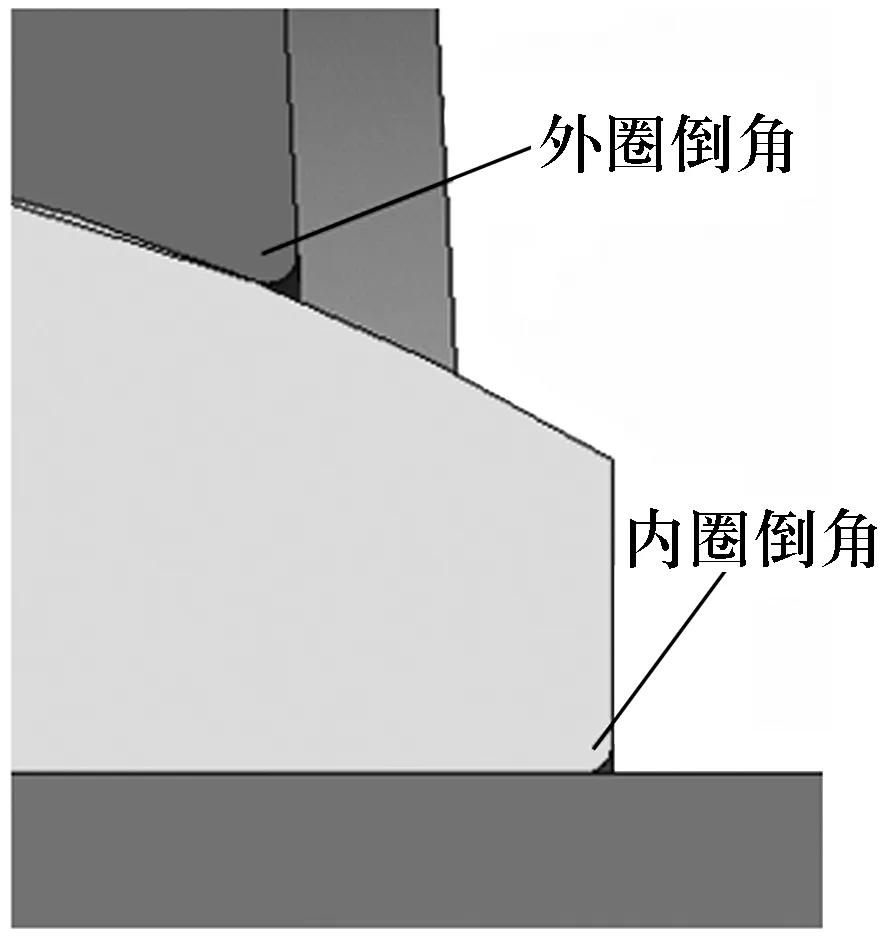
图3 考虑过渡角后的结构

表1 自润滑向心关节轴承材料主要参数

在极限静载荷776 kN下，考察外圈偏斜角在0～3°范围内对关节轴承应力场分布的影响。关节轴承应力场分布如图4，图5所示。

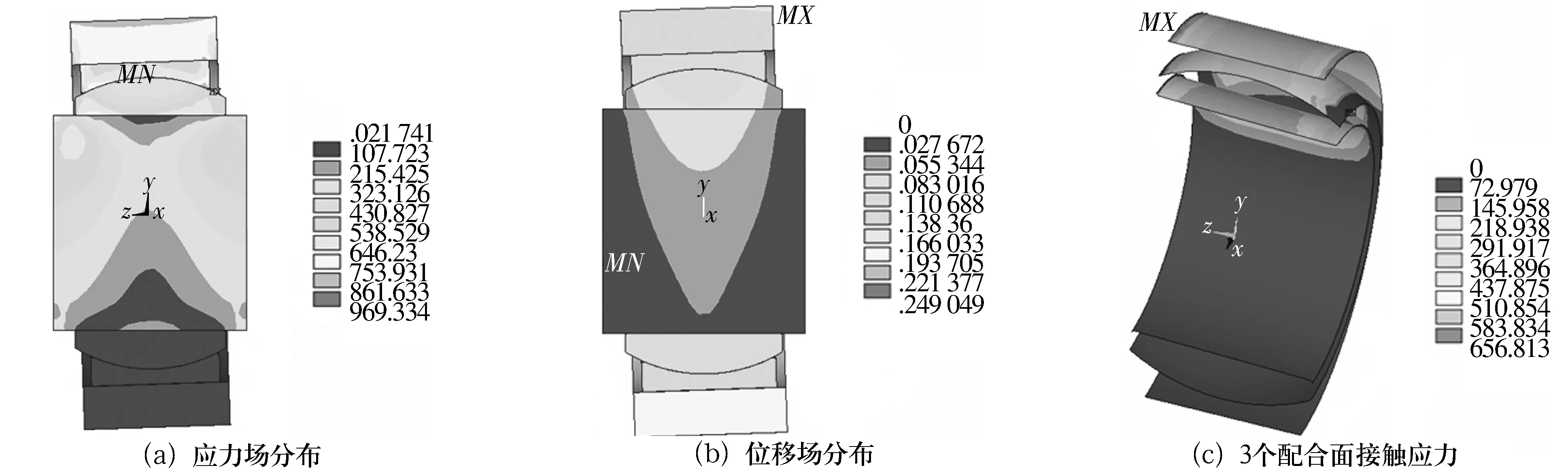
图4 偏斜角为2°时整体分析结果

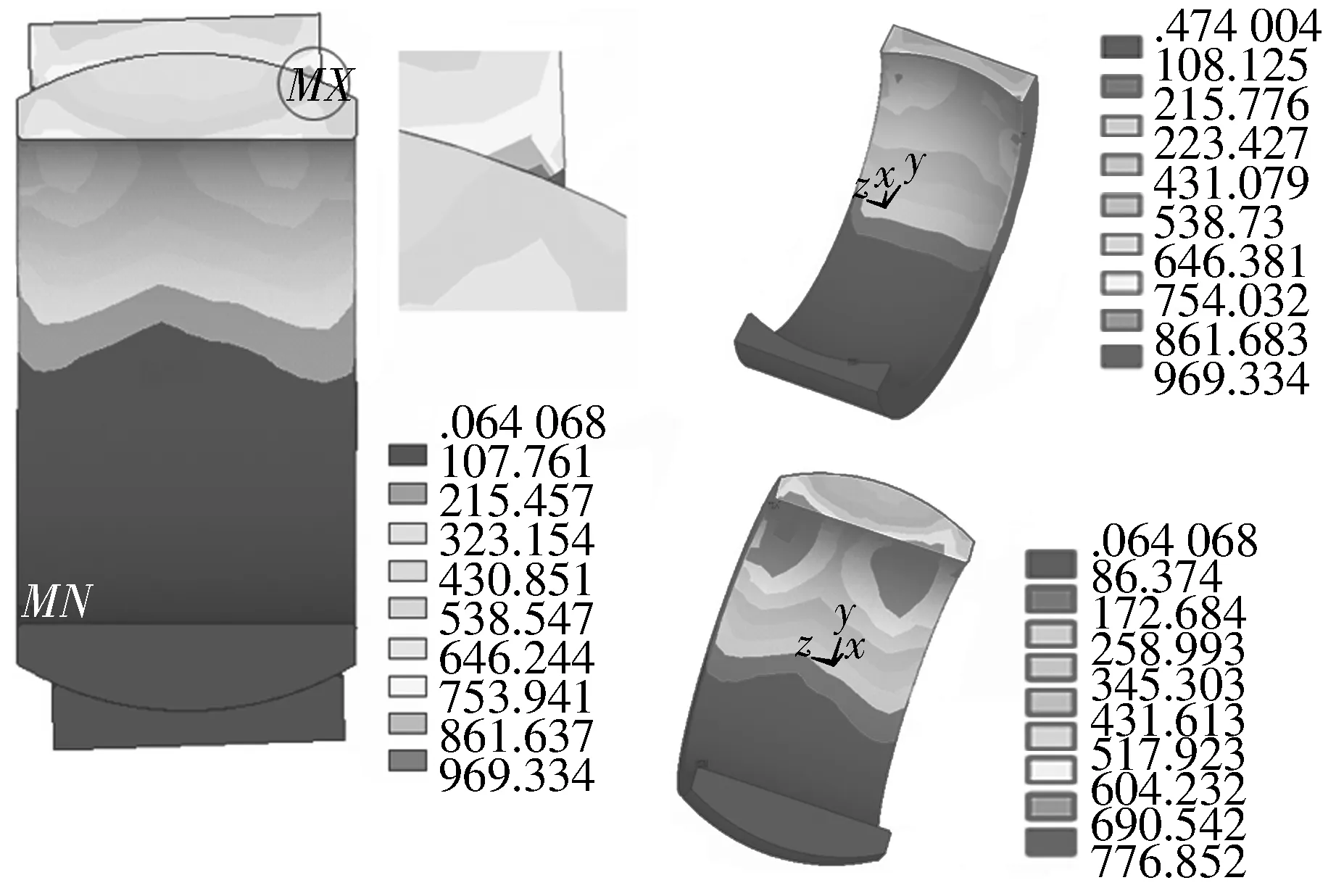
图5 内、外圈应力场分布及局部应力集中现象

从图中可以看出，在2°偏斜角下整体应力场分布明显不同于无偏斜工况下的应力场分布。偏斜角的存在使得在极限静载荷下，内、外圈的接触位置和作用力大小发生变化，由于受力不再是沿着中间位置对称分布，而使得在偏斜方向承受更大的接触力，而在另一侧则接触力相对减小。由于受力的不对称而在内、外圈的两端接触处出现明显应力集中现象，其应力值明显高于无偏斜工况下的最大应力值。

图6和图7分别给出不同偏斜角度下外圈剖面弧长处的等效应力和最大等效应力值曲线。可以看出在偏斜工况下，外圈边缘部位会产生明显的应力集中现象，在0～1.5°范围内随着偏斜角的增大，边缘的应力集中也呈增大趋势，与无偏斜情况相比增加200 MPa左右；而在1.5°～3.0°范围内随着偏斜角的增大，边缘处的应力集中则呈下降趋势，其中极限角3°时的应力值与峰值应力相比下降大约50 MPa。

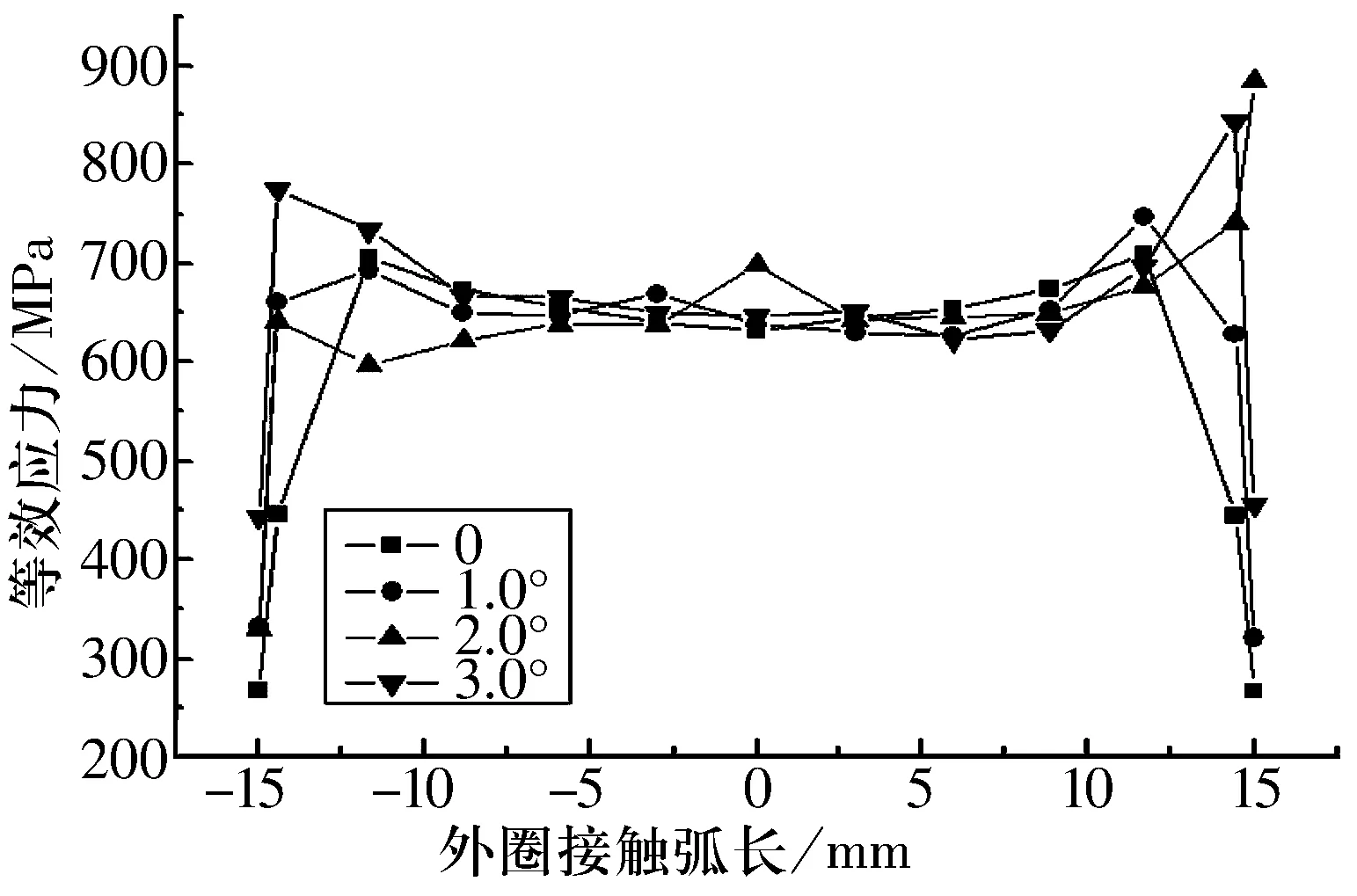
图6 不同偏斜角外圈接触弧长应力分布曲线

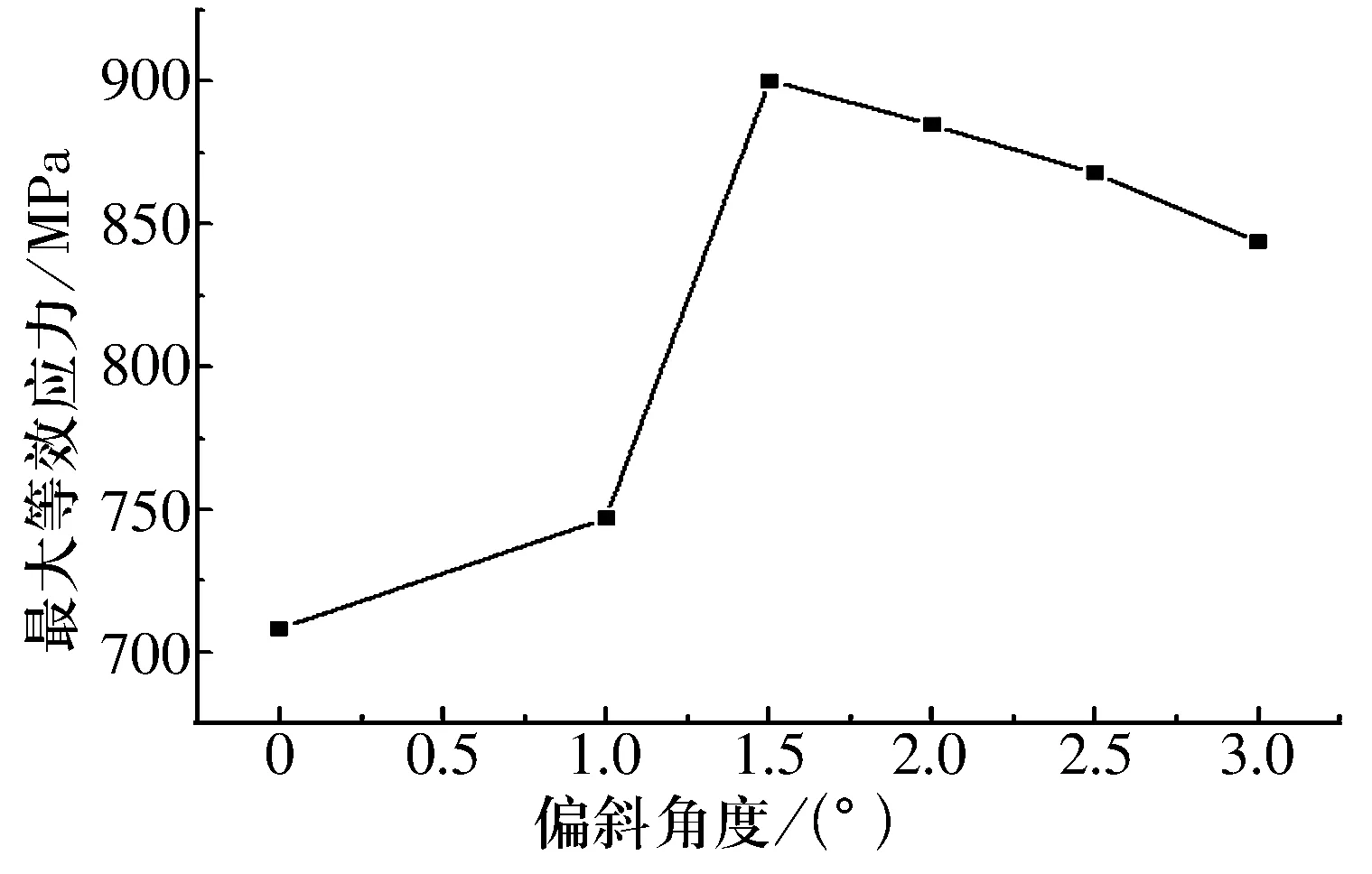
图7 不同偏斜角外圈最大应力曲线

4 结束语

对关节轴承在内、外圈相对偏斜工况下进行了应力场分析，结果表明，内、外圈的相对偏斜造成受力的不对称性，从而使内、外圈接触面端部出现明显应力集中，当偏斜角达到1.5°时，其应力值最大。应力集中的出现将增大局部的接触压力，加剧自润滑材料的磨损，造成关节轴承的过早失效，因此在实际使用中，要合理控制关节轴承的偏心，避免发生过大的应力集中现象。