EMD与二阶循环平稳分析在电动机轴承故障诊断中的应用

王小卉，杨洁明

（1.湛江师范学院 机电工程系，广东 湛江 524048；2.太原理工大学 机电研究所，太原 030024）

在各种机械故障中，由于轴承而发生故障的概率很高。轴承故障早期一般表现为内圈、外圈或滚动体的局部点蚀，随着轴承的运转，由于滚动体与内、外圈冲击而产生振动，这时的振动频率为轴承各部分的固有频率［1］，与此同时还有一个轴承旋转周期，此周期大于冲击产生的周期，对冲击产生调制作用，形成了调制信号［2］。轴承这种振动信号的二阶统计特征具有周期时变的特点，于是近年来人们开始转向研究循环平稳分析方法以实现轴承等旋转机械的故障诊断［3-4］。

实际上，故障信号不一定能直接从故障零件中取得，间接取得的信号又往往被强噪声覆盖，已有研究开始试用预处理和循环分析结合的方法处理信号［5］。考虑到电动机轴承振动信号的特性，用非平稳信号的EMD方法［6-7］，在分解重构信号后进行循环自相关，并应用谱相关切片集合分析法排除交叉干扰，以期达到快速准确提取故障特征的目的。

1 二阶循环平稳解调性能分析

如果信号x（t）满足条件：从一阶到二阶时变统计量都存在，且都是时间的周期函数，则该信号为二阶循环平稳信号。其表达式为：

式中：fz为载波频率，Hz；θ为相位角，rad；Ai为调节因子；ft为调制频率，Hz。

统计学中，信号x（t）的循环自相关函数表达式为：

式中：τ为时间滞后量；x*（t）为x（t）的共轭。假定信号满足时间遍历性，离散化后，该式可表达为：

由此可见Rx（t，τ）是关于时间t（固定τ）的周期为T0的函数。所以，可对（时变）相关函数Rx（t，τ）做Fourier展开，并且取a＝m／T0（循环频率），其中m为整数（m＝1，2，3，…），得到：

由上式可推知：循环自相关函数的非零值只存在于循环频率等于调制频率及其2倍频、2倍载波频率、2倍载波频率与调制频率及其2倍频的和差等地方，而在其他地方均为零［6］。

以（1）式所表达的信号为例，为方便分析，取n＝1（即i＝1），取Ai＝1.5，ft＝15，fz＝100，θ＝30，设信号：x1＝x（t），x2＝x（t）+0.8n（t），x3＝x（t）+0.8wgn，x4＝x（t）+1.5n（t）+1.5wgn。

其中n（t）为噪声服从正态分布的随机平稳遍历白噪声，wgn为Gauss噪声。

用循环自相关三维图分析可实现调制信号的解调，且可利用循环频率域高、低频率段内得到的信息进行相互验证，排除干扰。但三维图运算量大，信息冗余。二维的循环自相关切片分析得到的信息与三维图一致，如图1所示。在信号x1到x4，τ＝0时的循环自相关切片图中可以发现，循环频率信息分布在循环频率域高、低两个不同的频段。

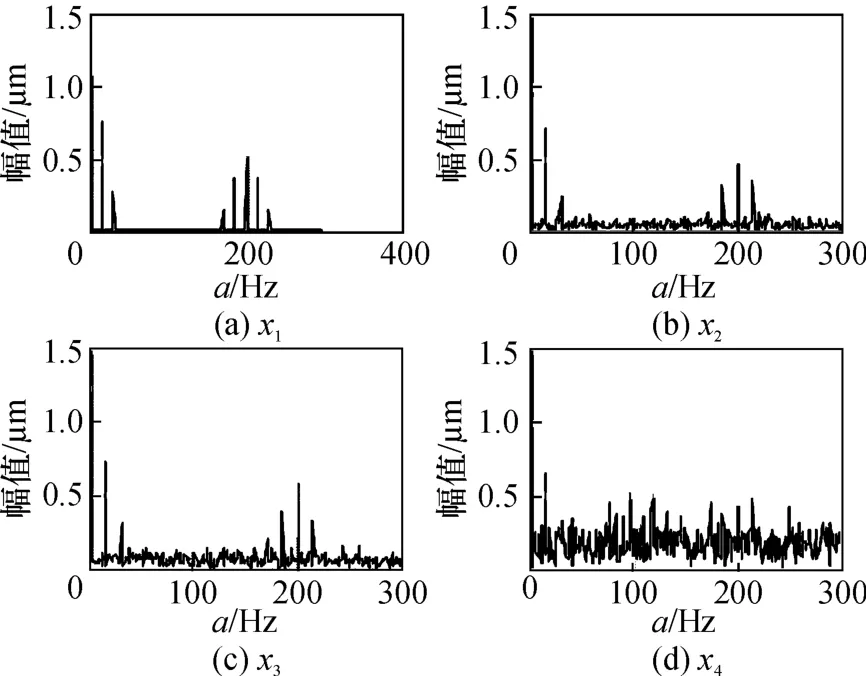
图1 信号x1，x2，x3，x4的循环自相关单切片（τ＝0）

在低频段仅含调制频率信息15 Hz，30 Hz（ft，2ft）；高频段既有调制频率也有载波频率的信息，200 Hz，（200±15）Hz，（200±30）Hz，（2fz，2fz±ft，2fz±2ft）。图1b与图1c分别是带有普通噪声x2和Gauss噪声信号x3的循环相关分析切片，说明循环平稳分析对普通与Guass噪声均有免疫性。但强噪声下单独使用循环平稳分析就难以排除干扰了，图1d是含Gauss强噪声信号x4的循环相关切片图，循环频率被完全覆盖。上述说明，二维循环平稳分析虽然有噪声免疫功能，但在强噪声下仍难以提取循环特征频率，抗干扰能力差。

2 强噪声信号的EMD预处理

实际采集到的信号会带有很强的噪声干扰，此时单用平稳分析很难达到预期诊断效果（图1d），这就需要选择一种适用于非平稳信号的消噪方法。

经验模态分解算法（EMD）基于信号的局部特征时间尺度，可把信号分解为若干个基本模式分量（IMF）之和，分解出的各个IMF分量突出了数据的局部特征，是一种自适应的信号分解方法，具有很高的信噪比，适用于非平稳、非线性过程，可采用EMD方法对振动信号进行预处理。设计的基于EMD的消噪步骤如下：

（1）提取本征函数IMF（ci）。分解信号x4，得出前6项IMF。

（2）对每项IMF分别作FFT变换，根据图2显示各模态分量的频率分布，可判别c2～c5的频率范围为10～250 Hz，包含了信号x4的所有特征频率（200 Hz，200 Hz±15 Hz，30 Hz等）。

图2 原信号及本征函数c1～c5 FFT图

（3）选用c2～c5进行信号重构，即使x4＝c2+c3+c4+c5（相当于带通滤波）。做重构信号τ＝0处的循环自相关切片得到图3，原来被噪声湮灭的载波频率（200 Hz）和调制频率（15 Hz）都能反映出来，与图1d比较，证实了EMD分解重构的消噪效果。

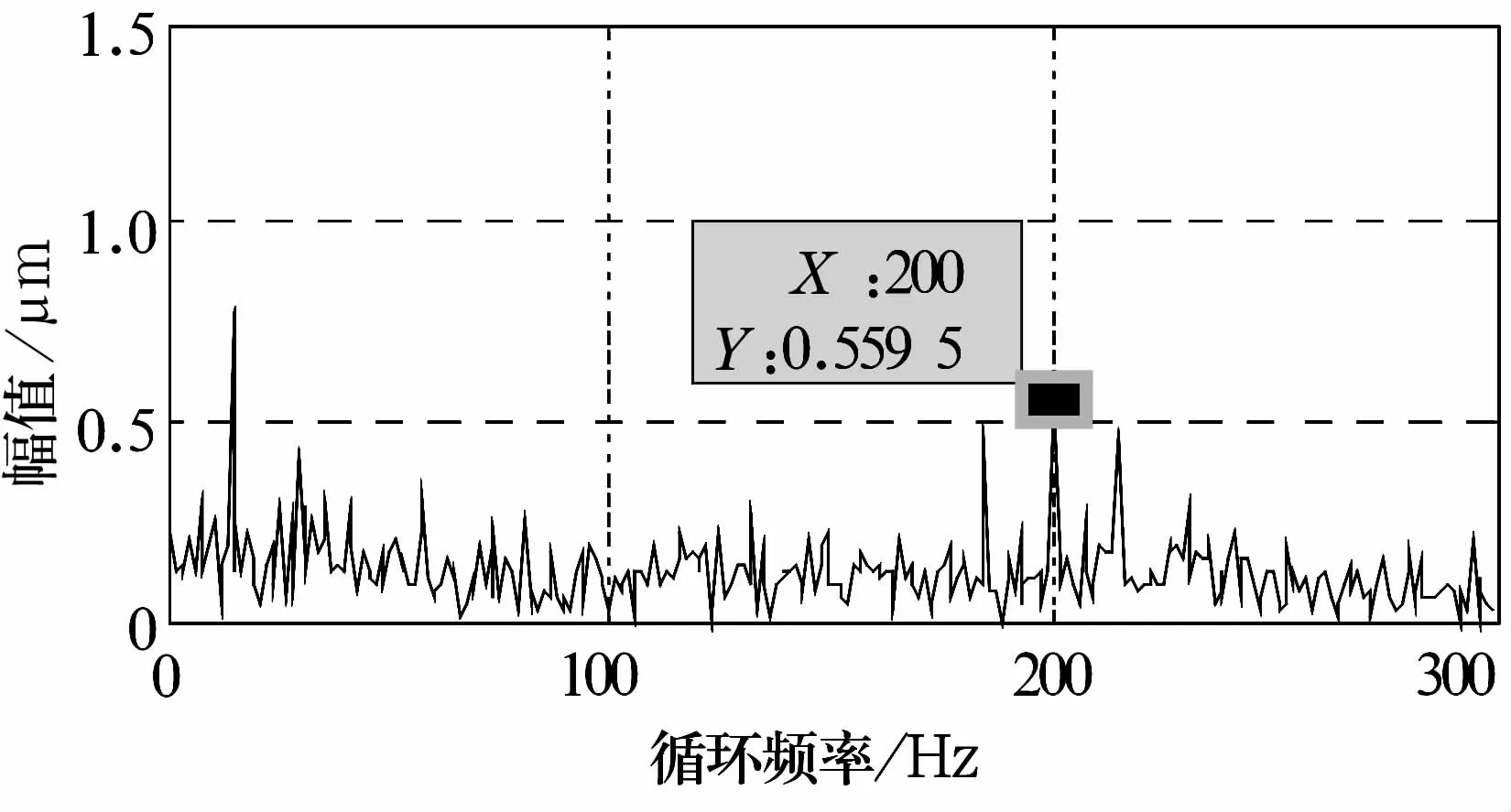
图3 重构信号的循环自相关切片

3 轴承故障试验分析

3.1 故障说明

试验采用Y160M2-8型电动机轴承故障试验台：主要设备有压电式加速度传感器、KISTLER5134型耦合器、DEWEtron十六通道信号采集器、磁粉制动器、齿轮箱、加载机构和电源。试验对象为6309型轴承。

试验数据如下：钢球直径Dw＝17.5 mm，球组节圆直径Dpw＝72.5 mm，钢球数Z＝8，接触角α＝0，试验时外圈固定不动，用涡流位移传感器测得主轴转速为715 r／min，转频fr＝11.9 Hz。计算［5］可得：内圈通过频率fi＝59 Hz，外圈通过频率fe＝36 Hz，钢球通过频率fb＝23.2 Hz，保持架旋转频率fc＝4.5 Hz。

如果某部位出现点蚀，循环统计量在相应的频率处出现能量峰值，据此可判别故障部位。

3.2 故障的分析及诊断

采集数据前，将多套6309型轴承进行轻度人为破坏，分别构成轻微的钢球故障、内圈故障、外圈故障及混合故障，以模拟工况下的各种早期故障。此处分析内圈故障轴承运转时从电动机端盖间接采集的信号。

电动机轴承的运行特点决定了其振动信号具有一定的二阶循环平稳性。故可以利用循环平稳分析来提取故障信息。

由第1节分析的结论可以得出在τ＝0时的谱相关切片的低频处有ft，2ft甚至3ft出现峰值。在整个轴承系统中，轴承如果出现故障，其产生的故障频率可作为载波频率，被转频调制；同时又作为调制频率，去调制系统频率（系统频率大概为1 560 Hz）。这里所提的切片集合分析的前提就是依据第2种情况，即将各种故障特征频率视为调制频率，假如此特征频率处的谱相关单切片图上有相应频率出现峰值，那么此频率则可以确定为故障频率。这种方法的特点是针对性强，运算量很小，在普通配置的计算机上便能实现。具体步骤为：

（1）消噪处理。试验信号只能间接由电动机轴承端盖采集，不是直接从故障轴承中采集，干扰很大。故先用EMD对内圈故障信号进行分解，选用本征函数c2～c5重构。

（2）做重构信号τ＝0处的循环自相关切片分析（图4）。可以看出峰值出现在内圈故障频率58 Hz，45 Hz和71 Hz（约为内圈故障频率的1倍边频59 Hz±11.9 Hz）处，也能发现120 Hz（约为2倍内圈故障频率），但也有很多未知的干扰频率，如29 Hz，48 Hz等亦出现峰值。

图4 处理后信号循环自相关单切片图

（3）对图4中出现峰值的频率处做循环谱密度切片集合分析，以排除干扰。如果是循环频率，在SCD谱图中会出现相应信息，若不是则为干扰，可以排除。由图5可见，在a＝29 Hz中没有出现相应的频率，进而被排除（同理48 Hz也被排除）。而在a＝59 Hz中则可明显发现60 Hz的信息，再次验证此轴承发生了内圈故障。

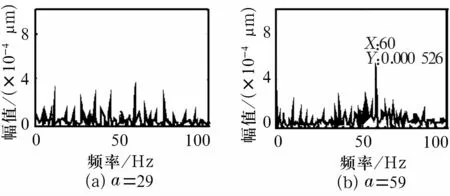
图5 峰值频率的循环谱切片集合分析

4 结束语

二阶循环平稳分析对噪声有免疫性，可实现故障特征分量分离，但在现场采集信号时，间接采集的轴承早期故障信号容易湮没在噪声中，EMD算法对信号分解重构进行消噪，基本达到预期效果。

通过试验证明EMD消噪与二阶SCA和SCD的综合分析法结合能有效排除故障信号中的干扰频率，提取微弱故障信息，此分析用到的仅是二维谱图，相比运算量庞大、信息冗余的三维谱图，此法的运算速度大大提高，能实现轴承早期故障的快速诊断，兼顾了效率与准确率。