相位信息在电绝缘系统参数测量中的应用

江守和 ，周保华 ，唐 君 ，童 刚

(1.山东出入境检验检疫局，山东 青岛 266002；2.中石油东北炼化工程有限公司财务处，辽宁 沈阳 110016；3.青岛科技大学 自动化与电子工程学院，山东 青岛 266042)

基于图像处理技术的电缆绝缘层参数测量系统实现了电缆参数测量的自动化，其测量过程简单、测量数据精确，可实现大批量电缆绝缘层数据测量。其原理为：(1)利用VC++编程测量系统软件，并通过CCD摄像头将被显微镜放大后的电缆层界面图像采集到电脑中，记录显微镜放大倍数；(2)图像经过去噪、二值化后，通过边缘检测算法提取电缆绝缘层封闭边缘，参考显微镜放大倍数，测量以像素为单位的电缆层厚度和直径等参数，并最终转化为实际物理长度，打印输出。本测量系统中，如何有效地提取电缆绝缘层封闭边缘显然非常重要。

数字图像的边缘检测是图像分割、目标区域识别、区域形状提取等图像分析领域中十分重要的基础[1]。大多数的图像特征检测算法都是基于图像亮度梯度进行的，而基于梯度的边缘检测算法存在很多局限性。由于图像常常受到随机噪声的干扰，所以在进行边缘检测时通常会把噪声当成边缘检测出来(即伪边缘)，而真正的边缘也因受到噪声的干扰并没有被检测出来，得到的边缘往往存在着缺口、毛刺等缺陷。

显然，带有缺口、毛刺的电缆绝缘层图像会给本系统带来较大误差，甚至错误。因此，边缘检测方法对于本测量系统至关重要。本文将介绍基于相位信息的图像边缘检测方法——相位一致性方法，推导其理论基础，并通过Matlab仿真结果说明基于相位信息的边缘检测算法的优越性。

1 相位一致性定义

相位一致性是指将图像傅里叶分量相位最一致的点作为特征点，它不但能够通过观察相位一致性高的点检测到阶跃特征、线特征以及屋顶特征等亮度特征，而且能够检测到由于人类视觉感知特性而产生的马赫带现象。

设一维信号为F(x)，则其傅里叶级数展开为：

式中，An表示第n次谐波余弦分量的幅值，ω是常数，φλ为第 n次分量的相位偏移量，而函数φn(x)表示 x点的傅里叶分量的局部相位。

对 F(x)进行 Hilbert变换后，可以得到信号 H(x)，其相位会发生90°的偏移，但幅值不会改变。

如果将 F(x)作为一个复信号的实部，H(x)作为虚部，可以构成一个复平面内的复信号：

Morrone[2]和 Owens[3]定义了相位一致性函数如式(4)所示：

假定信号的边界在相位一致性值较大的地方出现，相位一致性值 PC(x)在 0～1之间变化，1表示检测到了非常显著的边缘信息，而0表示没有检测到任何信息。

虽然利用相位一致性检测的边缘信号效果尚可，但是对信号频率分解的计算过程却非常复杂，实时性较差，所以对其进一步简化，得到近似模型，即局部能量模型。

2 局部能量估计

由于人类的视觉系统类似于一对奇偶滤波器组进行卷积积分，并且对其输出进行求和运算，所以局部能量的定义为信号平方与其Hilebert变换平方和的平方根，定义式如下：

式中 I(x)表示某一维信号，H(x)表示 I(x)的 Hilbert变换。函数的Hilbert变换与其傅里叶分量的幅值相同，对于正频率来说，每一分量的相位相移π/2，而对于负频率来说，每一个分量的相位相移-π/2。

Venkatesh和Owens指出，局部能量的两部分可以由信号与正交奇对称的滤波器M0和正交偶对称的滤波器Me的卷积来估计。数字图像局部能量估计如式(6)所示：

Venkatesh和Owens证明了局部能量等于傅里叶变换各分量幅度之和与相位一致性的乘积：

即PC与E成正比关系，局部能量函数直接正比于相位一致性函数，可得：

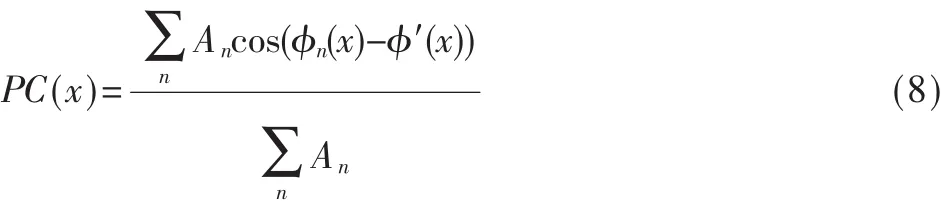
由式(8)可见，相位一致性函数等于局部能量函数与局部傅里叶分量从原点到端点的整个路径长度的比值。所以，相位一致性与信号的整体大小无关，保证了图像亮度和对比度的不变性。利用上述的推导结果对信号进行边缘检测，如图1所示。

图1 局部能量模型检测示意图

图1所展示的检测步骤主要是先对原始信号进行去均值(相当于经过式(6)的 Me滤波器)，然后再对信号做 Hilbert变换(相当于经过式(6)的 M0滤波器)，最后将其平方和开方，即可得到检测结果。从图中可以看出，此方法准确地检测出了信号比较明显的跳变边缘。

3 检测效果

任何一幅图像都包含着丰富的图像信息，如何提取这些信息并找出其中的特征就显得十分关键[4]。传统的边缘检测算法主要是利用空域微分算子通过卷积来完成。因为边缘的灰度值不连续，所以导数算子可以检测出这种灰度变化，通过对图像运用导数算子，突出图像中的局部边缘，然后将导数值作为相应点的边界强度，最后通过设置门限的方法提取边界点集。例如Sobel算子、Prewitt算子等，它们的共同特性是[5]：对原始图像按照像素的某邻域构造边缘，以检测出图像局部特性的不连续性。由于图像常常受到随机噪声的干扰，当使用这些算子进行边缘检测时，尽管它们具有计算量小的优点，但由于微分运算固有的特性，使得它们对噪声的干扰非常敏感，所以在进行边缘检测时通常会把噪声当成边缘检测出来(即伪边缘)，而真正的边缘也因为受到了噪声的干扰并没有被检测出来。因此，得到的边缘往往存在着缺口、毛刺等缺陷。在光照条件不理想或者亮度变化不剧烈的情况下，检测效果不理想，而且得到的结果还有可能出现同一个物体两侧各有一个边缘的情况。而基于相位一致性的边缘检测可以很好地解决这个问题。在光照不理想或者是图像亮度分布比较均匀的情况下能够得到较好的检测效果。图2所示的测试结果证明了这个结论，图像的边缘特征在图像的相位谱一致性上得到了很好地体现。

因此，相位一致性的提取结果与一般的灰度提取结果比较，可以看出利用相位一致性提取的线条细腻且封闭性好，更便于后续的参数测量与计算。而且对于对比度不同的原始图像，利用相位一致性检测的边缘效果图明显比Sobel算子检测的清晰。所以本系统采用相位一致性的方法来提取边缘轮廓。

4 系统实现及数据分析

将基于相位信息的边缘检测算法应用到电缆绝缘层测量系统中来提取图像的边缘特征信息，其轮廓提取模块的运行界面如图3所示。从图中可以看出：

(1)图像中检测出的电缆绝缘层的边缘轮廓，其伪边缘很少，使整个边缘轮廓更加完整光滑。

(2)图像中的像素值在边缘处分布比较均匀。

(3)检测到的电缆绝缘层边缘轮廓较细腻且封闭性良好，有利于提高测量的精确度。

系统中的参数测量模块原理为：搜索整个电缆绝缘层封闭边缘，得到多组等分的内外边缘之差，比如每1度得到1组边缘之差，共360组。系统将其转换为以毫米为计量单位的长度，并根据图像采集前得到的显微镜放大倍数，即电缆绝缘层图像放大倍数k，最终得到电缆绝缘层真实的物理长度。

由国标电缆绝缘和护套材料通用试验方法[6]可知，计量和检定部门对电缆绝缘层厚度等尺寸的测量仍然采用传统的基于机械投影仪的人工测量方法。一般的机械投影仪放大倍率在10倍以上，对于最普通的类型，如测量单芯圆形电缆绝缘层厚度，应将电缆图像移至视场中央，每隔60°测量对称的三对点，记录每个位置电缆内外层读数，求出6组数据中的最小值、算术平均值分别作为电缆绝缘层最小厚度和平均厚度。利用电缆绝缘层参数测量系统模拟国标中的测量过程，仅仅取出依次相差60°的6组电缆边缘之差，并将结果输出到word中，测量结果如表1所示。

显然，使用电缆绝缘层测量系统测量电缆参数操作简单、自动化程度高，较好地避免了人为主观因素的影响。通过多次试验结果分析可知，基于相位一致性算法的电缆绝缘层测量系统测量精度得到了进一步提高，与标准件相比，能够满足误差不超过0.01 mm的规定[6]，验证了基于相位信息的边缘检测算法对本测量系统的重要性。

表1 数据输出结果

图像边缘检测分为两大类，基于梯度信息的边缘检测和基于相位信息的边缘检测，而基于相位一致性准则检测图像中的边缘较之常规梯度计算方法更加可靠。相位一致性的大小与局部能量成正比，可视为对局部能量进行的归一化处理，从而可通过求取全局极值避免求解局部极值，也使得图像边缘的检测不再受光照强度的影响。本文以电缆绝缘层厚度参数为测量对象，通过基于相位信息边缘检测算法提取其边缘。分析可知，基于相位信息的边缘检测算法抗噪能力强，检测到的图像边缘线条细腻且封闭性好，更有利于后续的边缘识别和参数测量。根据已测图像放大倍数可得到厚度真实值，测量数据符合国家要求，精度较高。因此，基于相位信息的边缘检测算法在电缆绝缘层测量系统中的应用具有很好的可行性。

[1]高成，董长虹，郭磊，等.Matlab图像处理与应用(第 2版)[M].北京：国防工业出版社，2007.

[2]MORRONE M C，OOWENS R A.Feature detection from local energy[J].Pattern Recognition Letters，1987(6):303-313.

[3]OWENS R A， VENKATESH S， ROSE J.Edge detection is a projection[J].Pattern Recognition Letter，1989(9):223-244.

[4]左飞，万晋森，刘航.Visual C++数字图像处理开发入门与编程实践[M].北京：电子工业出版社，2008.

[5]肖志涛，国澄明，侯正信，等.图像特征检测算法的分析与研究[J].中国图象图形学报，2004，9(12):1414-1420.

[6]GB/T 2951.1-1997.电缆绝缘和护套材料通用试验方法[S].1997.