G.729.1语音编码算法的改进及实现

刘丽群，黄 冰，宁瑞芳

(桂林电子科技大学 信息与通信学院，广西 桂林 541004)

G.729.1是基于分裂带宽的编码器，具有灵活的结构，通过利用正交镜像滤波器组分析和合成滤波器组不仅能够处理采样率为16 kHz的输入语音，还可以处理8 kHz采样率的输入语音，它是一个基于G.729的带宽扩展(50～7 000 Hz)的、8～32 Kb/s可分级编码器。 由编码器产生的比特流具有可分级性，包含了12个嵌入式层。第1层为核心层，其编码速率为 8 Kb/s，核心层与原有 G.729中的比特流形式相同，这使得G.729.1与G.729之间具有互操作性。第2层为窄带增强层，每层均在之前一层的基础上增加2 Kb/s的编码速率，编码速率分别为 14 Kb/s、16 Kb/s、18 Kb/s、20 Kb/s、22 Kb/s、24 Kb/s、26 Kb/s、28 Kb/s、30 Kb/s、32 Kb/s。 编码器的默认输 入为16 kHz采样，16 bit线性脉冲调制编码语音信号，也可对8 kHz采样的信号进行操作。解码器的输出可以为16 kHz或 8 kHz采样的 16 bit线性 PCM语音信号[1]。

G.729.1编解码器基于三阶段结构：嵌入式码本激励线性预测(CELP)编解码、时域带宽扩展(TDBWE)以及时域混叠消除(TDAC)的估计转换编解码。其中，嵌入式CELP阶段产生第1和第2层，生成8 Kb/s和12 Kb/s窄带合成信号(50～4 000 Hz)。TDBWE阶段产生在第3层，生成 14 Kb/s宽带输出信号(50～7 000 Hz)。TDAC阶段工作在改进离散余弦变换域(MDCT)，生成第4～12层，将信号从14 Kb/s提高到32 Kb/s。TDAC编解码同时代表50～4 000 Hz频带加权CELP编解码误码信号和 4 000～7 000 Hz频带输入信号。算法中处理帧长为20 ms，每帧宽带信号样点数为640[2]。

本文主要对其TDAC部分的MDCT变换进行改进并用程序实现。在G.729.1算法的时延中，用于MDCT分析(估计)的时延为20 ms，通过MDCT的快速算法来减少该部分的时延，从而提高算法的实时处理的性能。

改进的离散深余弦(MDCT)广泛应用于语音和音频编码、分析和研究滤波器的时域别名取消特性。这是一种最为繁琐的计算密集型算法，因此需要一种快速算法来实现，到目前为止，已经提出了多种快速算法来实现MDCT。在这其中许多算法推导变换的长度为N=2m。本文将介绍一种基于长度为N=5×2m的新方法。这种长度的变换已建议在语音和音频编码中使用，典型的采样速率为 8 kHz或 16 kHz， 帧延迟为 10 ms或 20 ms。ITUTG.729.1和3GPP2EVRC-WB以及新兴的ITU-TG..EVVBR标准中也提供了这种算法。本文对G.729.1中的MDCT引入了一种新的算法，该算法更简便和更易于实际应用，非常适合在语音算法中应用。

1 算法的基本原理

设{x(n)}，n=0，…，N-1代表输入采样序列，N 为帧长。在本文中，MDCT和IMDCT的定义如下：

式中，X(k)是 MDCT的系数，x(n)是重建样点。为了简便，本文中忽略了定义中的正常化因子，将(N/2×N)MDCT定义为矩阵M：

所以MDCT/IMDCT可以记为：

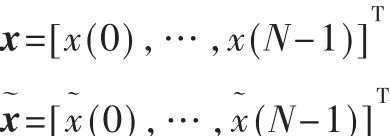
将N点的MDCT/IMDCT映射成为N/2点的DCT-IV如下[3]：

式中P为：

其中 IN/4和 JN/4为 N/4×N/4的单位矩阵及其相应的逆转矩阵。

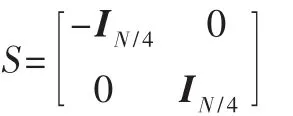
根据对称特性可以将DCT-IV矩阵映射成为DCT-Ⅱ矩阵，结果如下[4]：

式中，D是一个对角线矩阵，其元素为：

通过以上的变换可以看到，矩阵D和窗函数相乘后所得到的结果遵循IMDCT，这样就可以减少做N/2次的乘法，也即可以节省N/2的存储空间。MDCT可以通过逆变换从IMDCT中得到。然后进行逆DCT-Ⅱ变换。变换需要一种算法可以适合任意长度的序列。因此本文采用了既对频率状态进行抽取同时又可以执行递归直到DCT的长度为5点的方法。基于5点的DCT-Ⅱ是通过平面旋转的方法来取代系数x(3)与x(4)之间的3次乘法和3次加法，用同样的方法对x(0)和x(2)进行处理。该方法使处理的路径变短、结构的规律性增强、传输过程中数据的动态范围减少。基于5点的DCT-Ⅱ变换的方程如下：

逆DCT的变换方程如下：

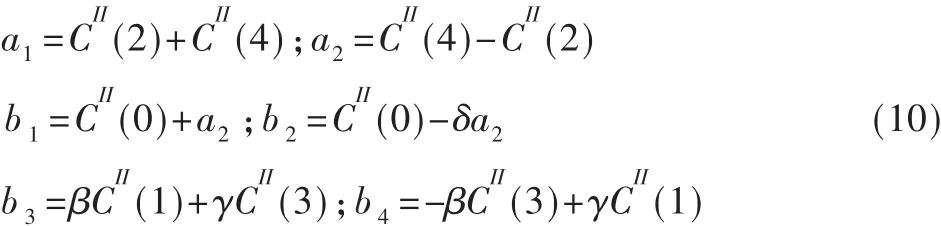
由于DCT-IV中的前项和后项乘法可以在MDCT和IMDCT分别合并窗函数，因此在许多应用实例中，MDCT都是使用下面的窗函数：

用该窗函数和传输因子整合成新的改进的窗函数，其表达式为：

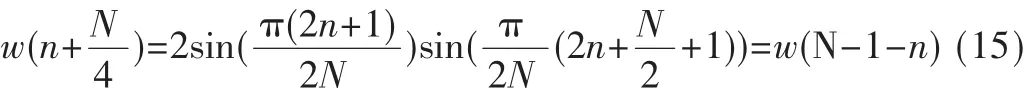
由此说明该窗是准对称的，与对称的正弦窗相比较，该窗也使用相同大小的存储空间。

2 算法的复杂度分析

设：N=5g2m(m≥2)和 NI=2m，RMF(N)和 RAF(N)分别代表N点MDCT的乘法和加法的复杂度，RMI(N)和RAI(N)分别代表N点IMDCT的乘法和加法的复杂度，RMD(5)和RAD(5)分别代表快速 5点 DCT-Ⅱ的乘法和加法的复杂度。进一步计算MDCT和IMDCT的复杂度用下面的计算公式：

由式(16)可知，MDCT/IMDCT算法的复杂度受到快速5点DCT-Ⅱ算法复杂度的限制。

3 算法的实现

经过改进后，新的MDCT变换算法如图1所示。图中，加窗所用的窗函数为一般情况下常使用的窗函数。

从以上分析可知，该算法的复杂度受到DCTII算法复杂度的限制，所以在做DCTII变换时用的是HEIDEMAN M T的基于5点的DCTII变换的算法。该算法进行5点的DCTII变换只需14次加法和4次乘法，而可以提高运算速度和节省运算时间。

图1 改进后新的MDCT变换算法

本文在G.729.1中的TDAC模块中引进了MDCT的快速算法，在G.729.1的默认模式下，该部分的时延为20 ms。通过使用本文中的方法进行改进，可以使该部分的时延降低约1/3，其存储空间也可节省约1/3。从而提高了该算法实现的实时性以及实际应用有了更大的可能性。在原来G.729.1的基础上实现了变速率，使该算法可以与G.729实现互操作，即该算法包含了G.729(因在原来G.729的基础上引入了TDBMW和TDAC技术)。

本改进算法的仿真结果(默认模式)如图2所示。

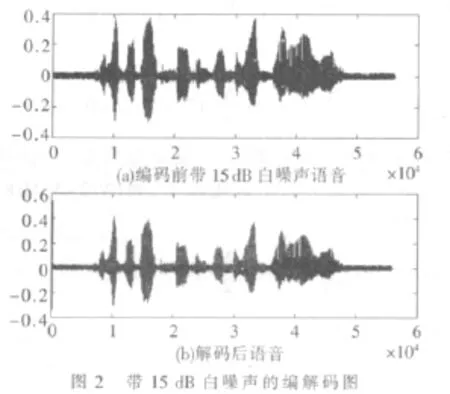
由图2可以看到，该算法的降噪性能并不是很理想，加15 dB白噪声的语音基本上不可懂，但是解码后的语音虽然包含一定的噪声，而人耳基本上可以识别。该算法在降噪方面还有一定改进的余地，G.729.1算法的改进还有很大的价值。

[1]ITU-T Rec.G.729.1.An 8-32 Kb/s scalable wideband coder bitstream interoperable with G.729.May.2006.

[2]贾懋珅，鲍长春，李锐.8～64 Kb/s超宽带嵌入式语音频编码方法[J].通信学报，2009(5).

[3]CHIVUKULA R K，REZNI Y A.Efficient implementation of a class of MDCT/IMDCT filterbanks for speech and audio coding applications[M].ICASSP，2008.

[4]HEIDEMAN M T.Computation of an odd-length DCT from a real-valued DFT of the same length[J].Signal Processing，IEEE Transactions， 1992，40(1):54-61.