类比法认识振动方向上存在恒力的简谐运动

杨 阳 刘成华

(江苏省前黄高级中学,江苏常州 213161)

类比是一种逻辑推理,也是抽象思维中的一种基本形式.它通过联想,把未知的事物(研究对象)对比寻常的、熟悉的事物(类比对象),然后依据两个对象之间存在着的某种类似或相似的关系,从已知对象具有的某种性质推出未知对象具有相应的性质.

类比推理有两个基本环节:

(1)选择类比对象.类比推理是以两个对象的比较为基础的,因此必须根据研究目的,从研究方法、形成结构、功能特征、因果联系等方面的相似之处出发,选择熟悉的、直观的事物作为类比对象.

(2)进行类比推理.如果对象 X有属性a,对象X′有属性a′,则对象 X有属性b时,对象 X′也可能有属性b′.

我们先回忆竖直弹簧振子的振动.

如图1(甲),当物体在平衡位置时弹簧伸长量为x0,重力和弹力相平衡,则 mg=kx0;

如图1(乙),当物体向下拉一小段距离 x(x＜x0),放手后物体所受合力 F=k(x0+x)-mg=kx,方向向上,指向平衡位置,而位移方向向下;

如图1(丙),物体在平衡位置上距离为 x时,物体所受合力F=mg-k(x0-x)=kx,方向向下,指向平衡位置,而位移方向向上.

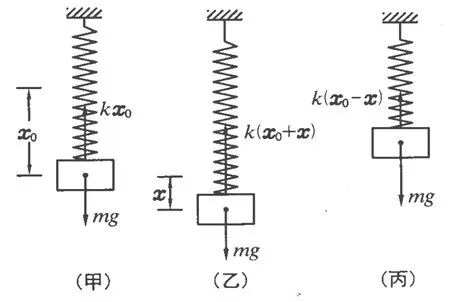
图1

从整个振动过程来分析,物体所受的合力跟它离平衡位置的位移x成正比,而方向始终跟位移相反,即F=-kx,所以竖直方向的弹簧振子的振动是简谐运动.

与水平弹簧振子的振动比较,在振动方向上的恒力——重力,改变了简谐运动的平衡位置,没有改变运动的性质.

竖直弹簧振子就是我们的类比对象.

例如,一些弹簧振子受到大小不变而方向随速度方向变化的滑动摩擦力、空气阻力等有阻力的振动问题,这与竖直弹簧振子受到的重力类似,因此通过类比分析,先来研究这个问题.

如图 2,在水平面上,劲度系数为 k的弹簧左端固定,右端振动的物体质量为m,与水平面的动摩擦因数为 μ.物体静止在O点时弹簧处于原长状态,现将弹簧拉长 A(弹簧弹力kA＞滑动摩擦力也是最大静摩擦力 f=μ mg)到达P点由静止释放.

物块在最右端P点静止释放,由于向左弹簧拉力F大于向右摩擦力 f,物块将向左加速运动,运动过程中摩擦阻力 f不变,与竖直弹簧振动类比,易证明物块做简谐运动,其平衡位置不是O点,而是在O点右方的O1点,设 OO1=x0,则振动振幅为 A1=A-x0(注意:振幅的计算是取平衡位置O1为起点),周期 T=但振动时间只有半个周期,即

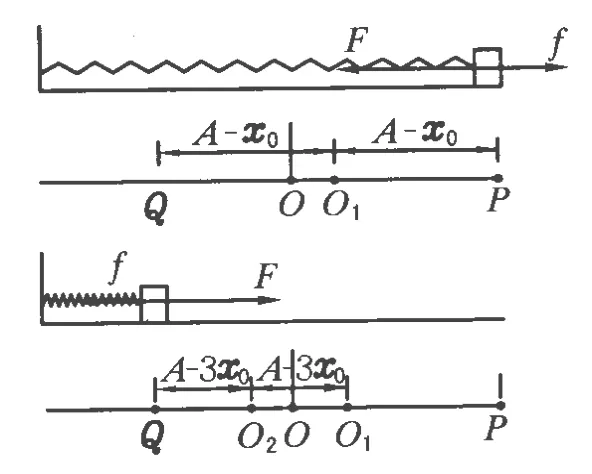
图2

物块到达最左端 Q点,如果向右的弹簧弹力F大于向左的摩擦力f,物块将向右加速运动,易知物块也是做简谐运动,但其平衡位置既不是O点,也不是O点右方的O1点,而是在 O点左方的O2点,且振幅为 A2=A1-2x0=A-3x0(注意:振幅的计算是取平衡位置 O2为起点),周期不变,时间不变,仍然为

物块到达最右端后,如果在 OO1的外侧,则向左弹簧拉力F一定大于向右摩擦力f,物体运动就重复着上面的振动过程,平衡位置 O1、O2不变,周期 T也不变,每次振动时间不变,只是每次变换方向后振幅都减少 2x0=即每次改变方向后的振幅为等差数列.

例1.一劲度系数为 k的水平轻质弹簧,一端固定,另一端连接一质量为m的物块,物块可在有摩擦的水平面上滑动,原长时位于O点,现拉离物块到距离O点为A的P点释放,如图3,设物块在第2次通过O点前,在O点左方停住.

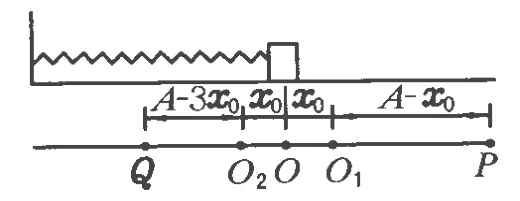
图3

(1)物块与桌面的摩擦因数μ应在什么范围内?

(2)求物块停住点与O点的最大距离,并回答这是不是物块在运动过程中所能到达的最大距离.(认为滑动摩擦因数与静摩擦因数相等)

分析:(1)物块只可能振动1次或2次.

(2)物块静止区域为O1O2,物块最远只能停在O2点,对应第(1)问第1种情况,此时应有 A1=A-x0=2x0,所以最远点距离 O点为这并不是物块在运动过程中所能到达的最大距离,在第(1)问第2种情况中物块可以越过O2点到达O2点左方.

下面再从能量的角度分析这种运动.

竖直弹簧振子在振动过程中动能与势能(包括重力势能和弹性势能)相互转化,总能量守恒,振幅不变,称为等幅振动、无阻尼振动.具有常量阻力的弹簧振动由于阻力的存在,阻力始终做负功,机械能减少,转化为内能,是阻尼振动,而且从前面的分析我们也可以看出其振幅是逐渐减小的.

但是我们知道阻力做功与振子走过的路程有关,完成振动 n次,其路程为 s=2n(A-nx0),阻力做负功-μ mgs,机械能减少 μ mgs,转化为内能 μ mgs=μ mg×2n(A-nx0),又第n次振动结束位置与O点距离即弹簧的伸长量(或缩短量)为 An-x0,由能量守恒定律得

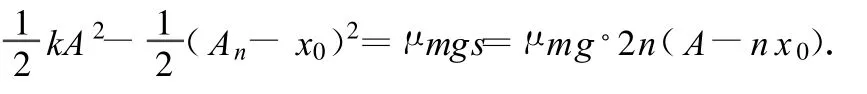
例 2.如图 4,将一水平放置的轻质弹簧(劲度系数为k)一端固定,另一端连接一质量为m的物块,物块与地面的滑动摩擦因数为μ,在弹簧伸长到最大距离瞬间,用手指弹物块使物块以速度 v0开始向墙运动.为保证物体多次往复运动,试确定速度v0.

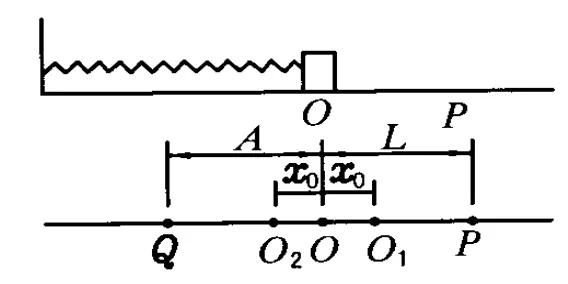
图4

分析:物块从P点向左运动时,根据能量守恒关系有

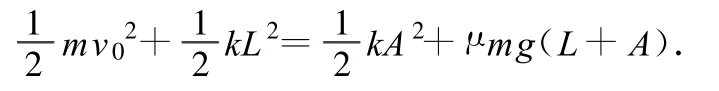
其中 A是弹簧的最大压缩量.

物块从 Q点向右运动时,由于保证物体多次往复运动,物块最远到达P点,因为 P点位置是弹簧最大伸长位置,如果到达 P点右侧弹簧将发生不可恢复的形变.则QO2≤O2P,即解得

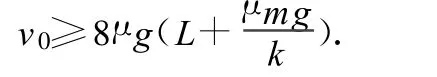
从前面的分析我们可以得到以下结论:

物块第n次振动振幅An=A-(2n-1)x0,呈现等差数列.(注意:振幅的计算是取平衡位置O1与 O2为起点);

第n次振动结束位置与O点距离即弹簧的伸长量(或缩短量)为 An-x0,也是等差数列;

振动路程s=2(A1+A2+…+An)=n(A1+An)=2n(A-nx0).

物块最终要静止,静止的位置不可能在区域O1O2以外,因为在区域O1O2以外弹簧弹力大于摩擦力,合外力不为零.静止的位置只可能在区域O1O2以内,或者说,物块如果在区域O1O2以内瞬间速度为零,物体就会静止.则

(1)如果第n次振动结束位置与O点距离An-x0＞x0,即 An＞2x0,物块第 n次振动结束位置在区域O1O2以外,将继续反向做第n+1次振动;

(2)如果第n次振动结束位置与O点距离An-x0≤x0,即 An≤2x0,物块第 n次振动结束位置在区域O1O2以内,并且停在区域 O1O2以内(An=2x0时对应停在平衡位置O1或O2).此时停止位置与O点距离即弹簧的伸长量(或缩短量)为 An-x0(x0＜An≤2x0)或者 x0-An(An≤x0).

图5

例3.图5是放置在水平面上的两根完全相同的轻质弹簧与质量为 m的物体组成的振子,每根弹簧的劲度系数均为k,弹簧的一端固定在墙上,另一端与物体相连接,物体与水平面间的静摩擦因数和滑动摩擦因数均为μ.当两弹簧恰为原长时,物体位于O点.现将物体向右拉离O点至x0处(不超过弹性限度),然后将物体由静止释放.设弹簧被压缩及拉长时其整体并不弯曲,一直保持在一直线上.现规定物体从最右端运动到最左端(或从最左端运动到最右端)为一个振动过程.求:

(1)从释放到物体停止运动,物体共进行了多少个振动过程?

(2)从释放到物体停止运动,物体共用了多少时间?

(3)物体最后停在什么位置?

(4)整个过程中物体克服摩擦力做了多少功?

分析:以弹簧为原长时物体(视作质点)的位置O为坐标原点,物体的运动轨迹为 x轴,并规定向右为正,如图6所示.

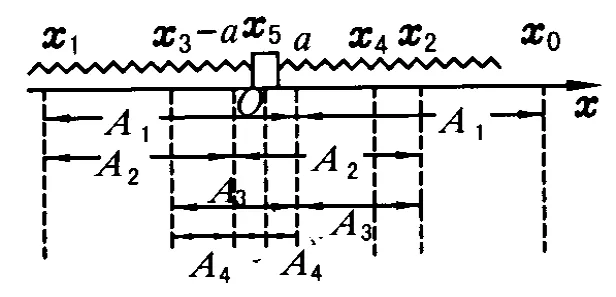
图6

物体在水平面上做直线运动.它受到弹力与摩擦力的作用,取力的正方向与 x的正方向一致,则物体运动时所受的合力为

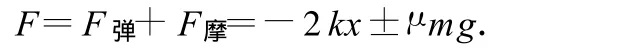
物体向左运动时,第 2项取正号,物体向右运动时,第2项取负号.

当物体向左(右)运动时,在 x=a(x=-a)处所受合外力为零,由此得

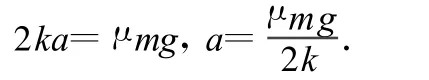
当 x处于±a之间的区域时,即当-a＜x＜a时,物体所受弹力的大小小于最大静摩擦力(亦为μ mg,与滑动摩擦力相同),在此区域物体一旦速度为零,便永久地停在那里,因为引起运动趋势的弹力将被静摩擦力抵消掉.

现在,物体由 x0处静止释放向左运动,物体所受的合外力为

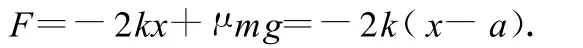
与竖直弹簧振子类比,物体在做简谐运动,其平衡点为x-a=0,即 x=a处,其振幅为

周期为

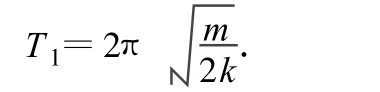
物体一直运动到最左端,即第1个振动过程的最末一点 x1,这时其速度成为零.x1点在 x=a点左方,与 x=a点的距离为振幅A1,则

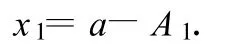
物体在x1点向右运动时即不再是上述的简谐运动,因为这时摩擦力反向,物体所受合力变为

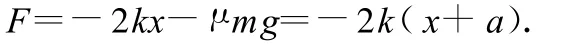
同样与竖直弹簧振子类比,这个新的简谐运动的平衡点在 x+a=0,即 x=-a处,其振幅为

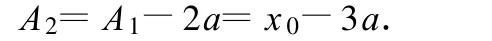
周期为

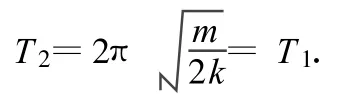
直到运动到右端第2个振动过程的最末点 x2=A2-a=x0-4a.第3个振动过程又是另一振幅的同频简谐运动,以后依此类推,由图6可以看出,有

而

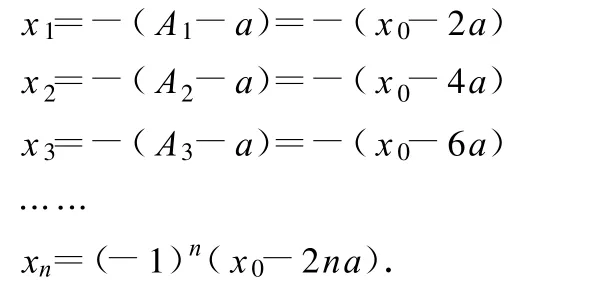
下面回答本题的4个问题:

若 x0＜a,则物体将于 x0处静止不动;若 x0＞a,则物体将做前面分析的简谐运动.

(1)物体停止运动的条件是当其位置 x满足-a＜x＜a时其速度为零,即某一个振动过程的末一点 xn落入-a与a之间,而前一振动过程的末端xn-1尚在此区间之外.

这样的 N应满足AN-1＞a,AN＜a,由An=x0-(2n-1)a知,上式即

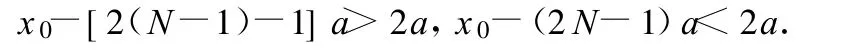
亦即 x0+a＞2Na,x0-a＜2Na.由此得

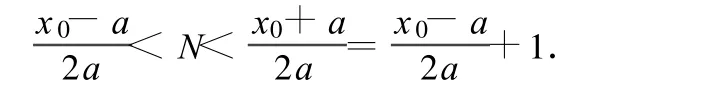
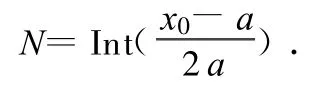
式中Int(C)即为C的整数部分.

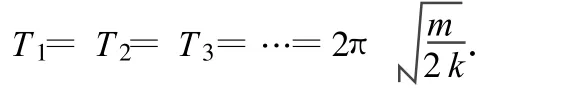
而每个振动过程均历时半个周期,因此物体在停止运动前共用时间为

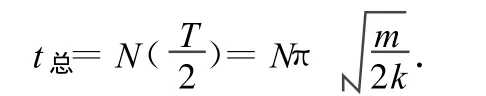
(3)物体停止的位置即为第 N个振动过程的最末点xN.xN可用An的通式计算得出xn=(-1)n(x0-2na),由此得xN=(-1)N(x0-2Na).

(4)物体克服摩擦力所做的功可有两种计算方法.

第1种:摩擦力所做的功等于物体开始时的能量与停止时能量之差,而这两个时刻物体只有弹性势能,于是

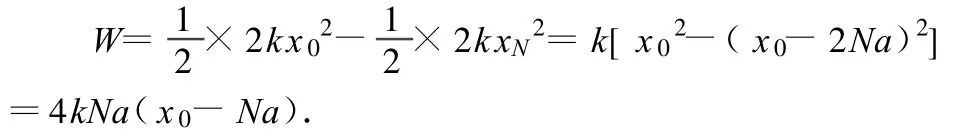
第2种:直接用摩擦力乘以物体走过的总路程

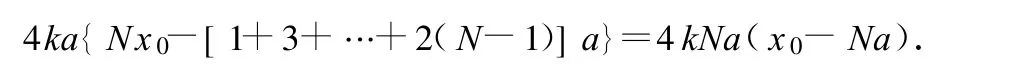
类比是科学研究中十分有用的一个方法.对于陌生的物理情景,通过与我们熟悉的模型类比,找出规律,比较相同点和不同点,是使学生快速理解掌握未知的陌生的物理情景的有效方法.