对斜面上的平抛运动图像的修正

邹 俊

(江苏省丹阳市吕叔湘中学,江苏丹阳 212300)

本刊2009年第9期刊出了“从高难到口算— —巧用求异思维妙解难题”一文中给出了斜面上平抛运动的4种巧妙解法,读后深受启发.笔者经过推敲后感到原文所配图有所不妥.在此提出我的意见,供大家参考.

原题.如图1所示,在倾角为θ的斜面顶端A处以初速度v0水平抛出一个小球,小球最后落在斜面上的另一点B上,空气阻力不计,求运动过程中小球离开斜面的最大距离H是多少?

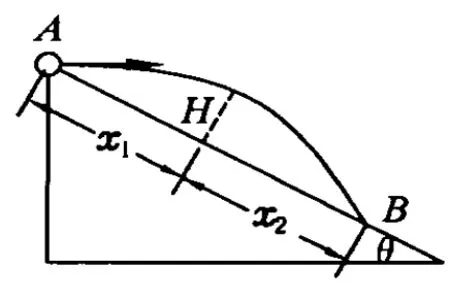
图1

图2

笔者认为图1所示的平抛物体的运动轨迹是错误的.读者可以注意到,小球在空中运动的轨迹以最高点为界的话,左右两段弧线几乎是对称的.该示意图不能反映小球真正的运动情况,小球的实际运动应该是离开斜面阶段沿斜面的位移 x1小些,靠近斜面阶段沿斜面的位移 x2大些,较为精确的的图应该如图2所示.

图3

我们可以借助原文解法分析,如图3小球经过速度和加速度的分解之后,小球的平抛运动就可以看作两个方向运动的合运动.y方向的运动为初速度v0y=v0sinθ,加速度 ay=gcosθ的先匀减速后匀加速运动,当 vy=0时,小球离斜面最远,x方向的运动为初速度v0x=v0cosθ,ax=gsinθ的匀加速运动.设小球抛出经过时间 t距离斜面最远,由于y方向是类竖直上抛运动,所以小球从离斜面最高点落到斜面上的时间也等于t.同时注意到小球 x方向有初速度,即得小球从运动到距离斜面最远过程中 x方向位移为

小球从距离斜面最远回到斜面过程中x方向的位移为

由平抛运动不难解出

把(3)式代入(1)、(2)式化简得

表1

从表1知道θ=37°时,x1只有约 x2的了,图像的修正就不容忽视.从学生理解问题的角度,教师也可以适当地夸大 x1和 x2的长度差异,引导学生思考运动分解后小球沿斜面运动的情况.本题中经过分解小球在沿斜面方向是初速度不为零的匀加速直线运动,而在水平地面上的斜抛运动,经过分解后小球在沿地面方向是个匀速直线运动.引导学生分析其中的差异,会增进学生使用运动的合成与分解规律解决问题的能力.