向心加速度表示速度方向变化的快慢吗?
徐 学 朱 斌
(1.江苏省苏州中学园区校,江苏苏州 215021; 2.江苏兴化安丰高级中学,江苏兴化 225766)
当物体做曲线运动时,加速度可以分解为沿着速度方向的切向加速度和垂直于速度方向的向心加速度,切向加速度改变速度的大小,向心加速度改变速度的方向.当物体做匀速圆周运动时,速度的大小将不发生变化.只存在改变速度方向的向心加速度,向心加速度的作用是只改变速度的方向.从加速度的物理意义来看,加速度是表示速度变化快慢的物理量.因此向心加速度的物理意义表示的是速度方向变化的快慢.果真如此吗?
日前笔者在高三物理的复习中遇到这样的一道题:
题目.甲、乙两个质点,分别做不同的圆周运动,下面的说法中正确的是
(A)线速度较大的质点,速度变化较快.
(B)角速度较大的质点,速度方向变化较快.
(C)向心加速度较大的质点,速度方向变化较快.
(D)向心加速度较大的质点,速度变化较快.

图1
分析1:许多学生选择了选项(B).他们认为物体在做圆周运动时,在Δt时间内,物体的速度由 v1变为 v2,如图1所示,把 v1平移至v1′,则 v1′与 v2之间的夹角为 Δθ,Δθ就是在Δt时间内速度方向的变化量就表示在单位时间内速度方向变化量,也表示速度方向变化的快慢.由图可知,弧 AB对应的圆心角 Δθ′=Δθ,而因此ω就表示速度方向变化快慢的物理量.
分析2:也有不少学生认为(C)选项正确.他们觉得加速度是表示速度变化快慢的物理量,加速度可以分解为切向加速度和向心加速度.切向加速度改变速度的大小,向心加速度仅改变速度的方向,所以向心加速度是表示速度方向变化快慢的物理量.在阳光出版社2009年10月份出版的《全品学练考》的第11页就是这样论述的“向心加速度就是反映速度方向变化快慢的物理量”.
两种分析看来都有道理.究竟是ω表示速度方向变化快慢呢?还是a表示速度方向变化快慢.
探究:如果我们设想这样的特例 ωA=ωB,则 TA=TB.在一个周期内两个物体速度方向均改变2π,所以两个物体速度方向变化快慢是一样的,如果 rA=2rB,则 a向A=rAωA2,a向B=rBωB2,则 a向A=2a向B,虽然 a向A>a向B,但是两者速度方向改变快慢却是一样的.因此向心加速度不能表示速度方向变化快慢.(C)选项是错误的.
那么为什么向心加速度不能表示速度方向变化快慢呢?
分析:如图2设物体做变速圆周运动,在Δt时间内,物体与圆心O连线扫过的圆心角为Δθ,在速度由 v1变化为v2,把 v1平移至 v1′,作出速度的变化量 Δv.物体的加速度把Δv沿着v2和垂直于 v2分解为Δv1和Δv2,向心加速度,当 Δt→0,则 sinΔθ≈Δθ,则上式所以速度方向改变的快慢ω除了与向心加速度有关,还与物体做圆周运动的半径r有关.在物体的运动半径 r没有确定的前提下“向心加速度表示速度方向变化快慢的物理量”是错误的.
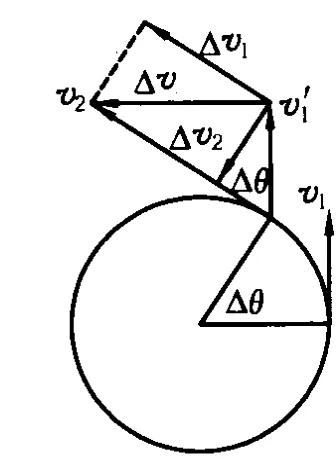
图2

图3
若物体做匀速圆周运动(v仅表现为方向改变)结论是否正确呢?如图3,可以看到,虽然速度 v仅表现为速度v的方向的变化,Δv是Δθ与v的乘积,Δv除了与速度方向改变量的大小Δθ有关,而且与物体的速度 v有关.而v=ω r,是与圆周运动的半径有关的物理量.物体的向心加速度仍旧是由 ω和r两个物理量共同决定,在物体的运动半径没有确定的前提下,向心加速度表示速度方向变化快慢这个结论也是错误的.
结论:物体的角速度是表示物体做圆周运动时速度方向变化快慢的物理量,物体的向心加速度不能表示物体做圆周运动的速度方向改变的快慢.仅当物体做圆周运动的半径一定时,才能表示物体速度方向变化的快慢.

