器材拣选决策的改进节约算法

葛 阳，王晓峰， 郝 冰，宁剑平 GE Yang,WANG Xiao-feng,HAO Bing,NING Jian-ping

（1.军械工程学院，河北 石家庄 050003；2.63869部队，吉林 白城 137001；3.76127部队，湖南 郴州 424202）

0 引 言

1 拣选作业的数学模型

假设： （1）货位间距为常数，h为货位高度，b为货位宽度，长度忽略不计。 （2）器材外形规则，周转货箱装箱能力仅与待装器材体积有关。 （3）器材摆放位置可视为货格的中心点上，货位坐标为（x,y ），表示位于第x层第y列。 （4）货箱容积大于任一货位内器材的体积。

符号： （xlk,ylk）——第l次取货，第k步巷道车停留在货架的第xlk层第ylk列；A（ i,j,m）——货架第i层第j列第m种器材库存数量 （已知）；B（ xik,yik,m）——第l次取货，第k步拣选第m种器材的数量；dm——调拨单中需要调拨的第m种器材的数量 （已知）；vm——第m种器材的体积 （已知）；V0——货箱的容积 （已知）。

假设巷道车在横向和纵向的速度是恒定的，影响拣选作业效率的主要因素就是巷道车行走距离的多少，所以优化的目标就是寻求一条最短的拣选路径。当拣选器材较多时，受拣货箱容积和承重的限制 （对于小件器材一般只考虑货箱容积的限制），可能无法一次完成拣选作业，需要分多次进行，因此，巷道车在整个拣选作业过程中所行走的距离就是进行每一次拣选路径的距离之和。

目标函数：

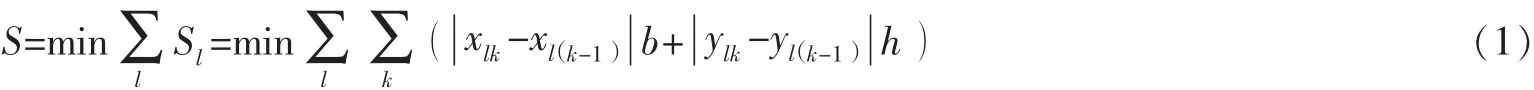
式 （1）中，S代表巷道车行走的最短距离，Sl表示第l次取货时，巷道车所走的距离，xlk-xl（k-1）b表示巷道车第l次第k步取货， 由货位 （xl（k-1）,yl（k-1））移动到货位 （xlk,ylk）时横向行走的距离， 同理ylk-yl（k-1）h表示纵向的行走距离。由于巷道车一般有两个电机驱动，一个负责横向移动，另外一个负责纵向移动，所以这里认为巷道车行走的距离就是巷道车在横向和纵向行走的距离之和。

约束条件：

每次拣选的器材体积之和小于等于货箱的容积，即：

拣选第m种器材的数量之和等于调拨单中第m种器材的数量，即：

对第i层第j列拣选的第m种器材的数量小于等于该货位上存放的第m种的数量，即：

货架存放的第m种器材的数量大于等于调拨单中该种器材的数量，即：

2 节约算法求解

拣选路径最优问题，已被证明是NP-难问题[2]，精确算法的计算量太大，一般采用近似算法或启发式算法，节约算法是一种常见的启发式算法，由于它简单实用在配送领域的路线规划上被广泛应用，本文将其引入到器材拣选作业中，以求得路径优化的满意解 （不一定是最优解）。

2.1 节约量公式

设巷道口为P0，N个货位分别是P1,P2,…,PN，已知其中任意两个货位 Pi和Pj之间的距离为 dij别为Pi和 Pj的坐标 ）。从巷道口开始拣选货位Pi和Pj，有两种方案，一是一次性完成两个货位的拣选后回到巷道口，二是往返两次分别拣选这两个货位，前者比后者行走距离的节约量为：

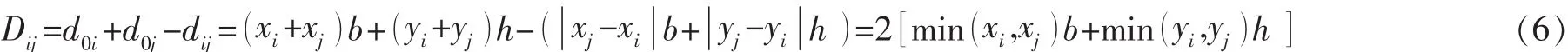
式 （6）就是著名的节约量公式。由推导结果可知，Dij≥0。

2.2 节约算法的思路

由于同一种器材可能存放于多个货位，入库年份也可能不同，如果随机拣选，入库较早的器材可能一直不被拣选到，随时间推移，器材过了保质期就难免报废，造成浪费。所以，首先要根据 “先进先出” （或 “用旧存新”）原则及式 （3）确定好待拣货位及数量，其次是将所有待拣货位两两组对，并计算其行走距离节约量，将节约量按由大到小顺序排列，选择节约量最大的两个货位，判断这两个货位待拣器材体积之和是否超过货箱的容积，如果不超过货箱的容积，则将这两个货位合并为一次拣选，如果超过货箱的容积，则不合并这两个货位，转而判断节约量稍小的另两个货位能否合并为一次拣选。直到所有可能合并为一次拣选的货位全部合并，最终得到巷道车行走距离优化的满意解。节约算法流程如图1所示。

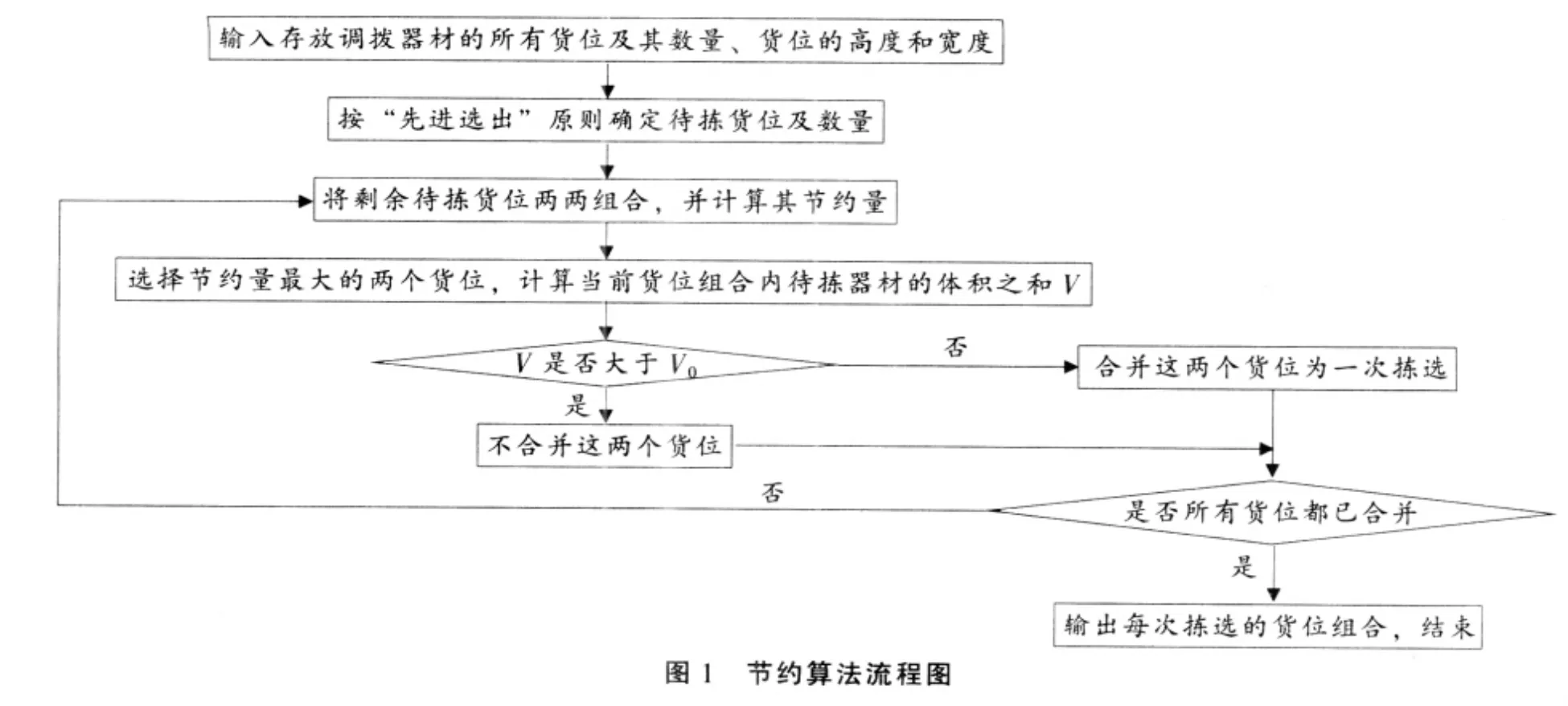
根据节约算法，3算例分析中的算例可得最终的拣选路线 （见表4）为：r1=（0→16→17→7→5→0 ）；r2=（0→8→15→6→0 ）； r3=（0→4→14→11→0 ）； r4=（0→2→3→0 ）； r5=（0→12→13→9→10→0）；r6=（0→1→0 ）。可以看出一共分6次拣选，巷道车行走总距离为534米。

2.3 节约算法的不足及改进

由3算例分析中的计算过程可以看出节约算法应用在器材拣选中还存在一些缺陷，需要改进。一是每个货位内的待拣器材数量不允许分割必须一次性拣完，这可能导致货箱不能装满，影响货箱容积的利用率，从而使拣选次数增加；二是每次拣选路线，货位都是按节约量的大小和货位序号进行排列的，货位的前后左右的位置可能较乱，造成巷道车在一次拣选过程中往复行走，使得行走距离增加，如算例中第1次拣选路线：r1=（0→16→17→7→5→0 ）， 巷道车行走的距离为178米， 如果按照 （0→7→17→16→5→0 ）顺序拣选， 则巷道车行走的距离为166米。所以需要对以上两点不足进行改进。

针对货位存放的待拣器材数量不能分割问题，本文提出以下改进思路：将待拣货位两两组合，并计算其节约量，选择节约量最大的两个货位：①如果它们存放的待拣器材体积之和小于货箱容积，则合并它们一次拣选，并进一步寻找与这两个货位之一合并带来最大节约量的货位，把这个货位也合并到当前次拣选路线上，直到该线路上待拣器材的体积之和等于或大于货箱容积，合并最后一个货位使得货箱刚好满载或不能再装其他器材。②如果这两个货位器材体积之和等于货箱的容积，则合并它们在一条线路上拣选。③如果这两个货位器材体积之和大于货箱容积，则合并它们在一条线路上拣选，并使货箱满载或不能再装其他器材，将剩余的器材和其他待拣货位组成一个新的拣选决策问题，重复上述方法，直到所有货位全部被合并。

针对巷道车在一次拣选过程可能多次往复问题，本文提出以下改进方法：对于M层N列的固定货架，令r为不大于M/2的最大整数；将1～r层货位按列号从小到大排序；将r+1～M层货位按列号从大到小排序；在每一次拣选过程中先拣选1～r层货位再拣选r+1～M层货位，则可避免巷道车往复问题。

改进的节约算法相比传统的节约算法：一是允许货位存放的待拣器材分多次拣选，提高货箱利用率；二是将每一次要拣选的货位进行排序，避免巷道车多次往复，减少其行走的距离。改进的节约算法具体流程如图2所示。

按改进的节约算法，再计算3算例分析中的实例，如表5所示，可得以下拣选路线：

r1= （0→8→7→17→16→0 ）； r2= （0→15→8→5→4→0 ）； r3= （0→6→4→14→11→12→13→0）；r4=（0→3→2→13→0 ）； r5=（0→1→13→9→10→0 ）， 共分5次拣选， 巷道车行走的总距离为492米。

3 算例分析

自动化立体器材仓库某一巷道货架共10行 （层）72列，货位高和宽均为1m，货箱容积为20dm3，根据器材调拨单要拣选5种器材，随机产生调拨单和器材货位对照表如表1所示 （为简化计算这里认为器材体积可直接相加）。要求制定拣选计划，使得拣选距离最短。

3.1 确定待拣货位

根据 “先进先出”原则和调拨单数量要求，可确定以下待拣货位及数量如表2所示。

3.2 计算节约量

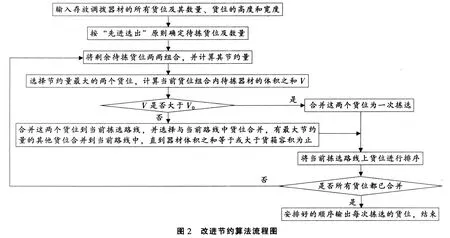
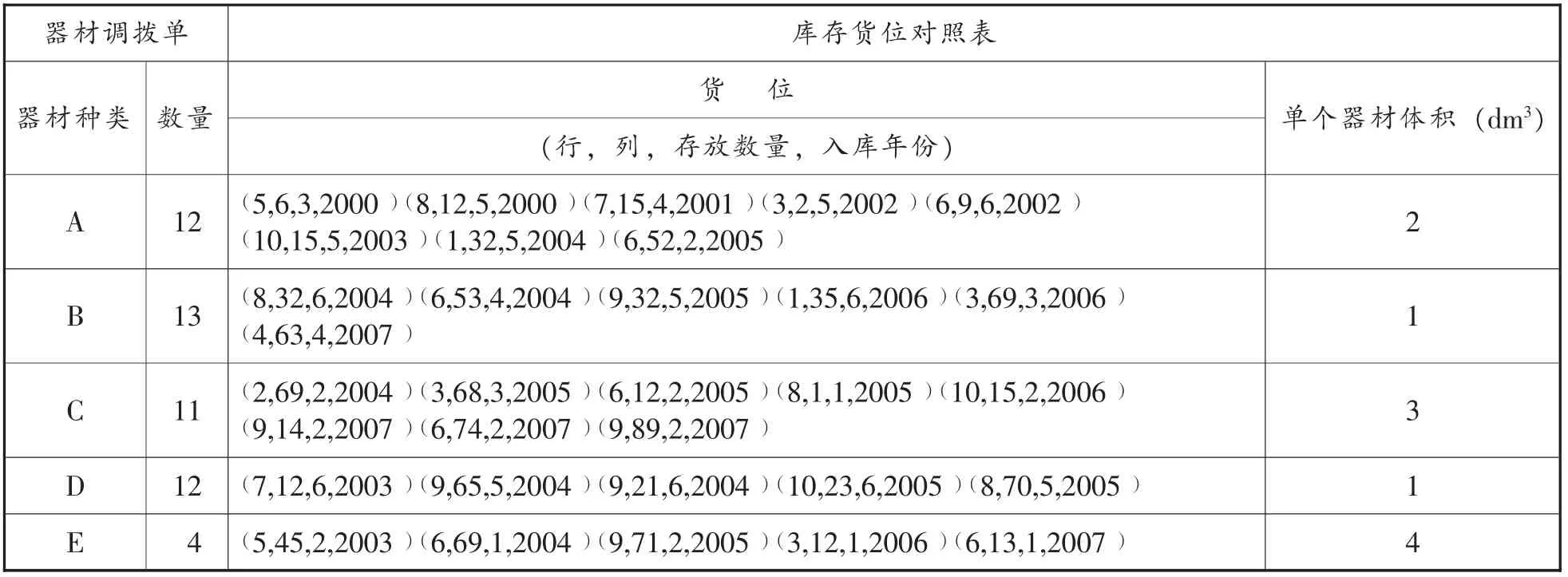
表1 器材调拨单及库存货位对照表

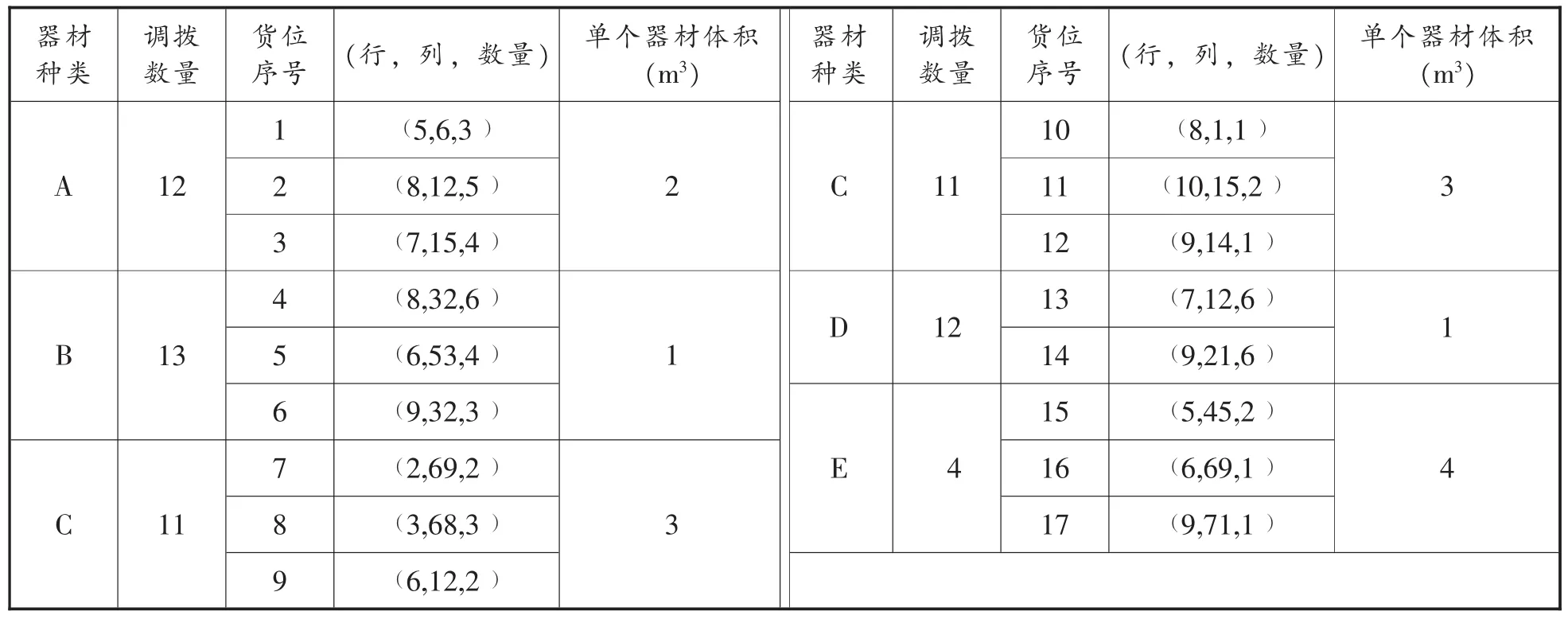
表2 待拣货位表

将待拣货位两两组对，计算距离节约量如表3所示。

3.3 节约算法求解

按照图1所示的节约算法流程及已确定的待拣货位和数量，可得表4所示决策结果 （具体步骤略）。

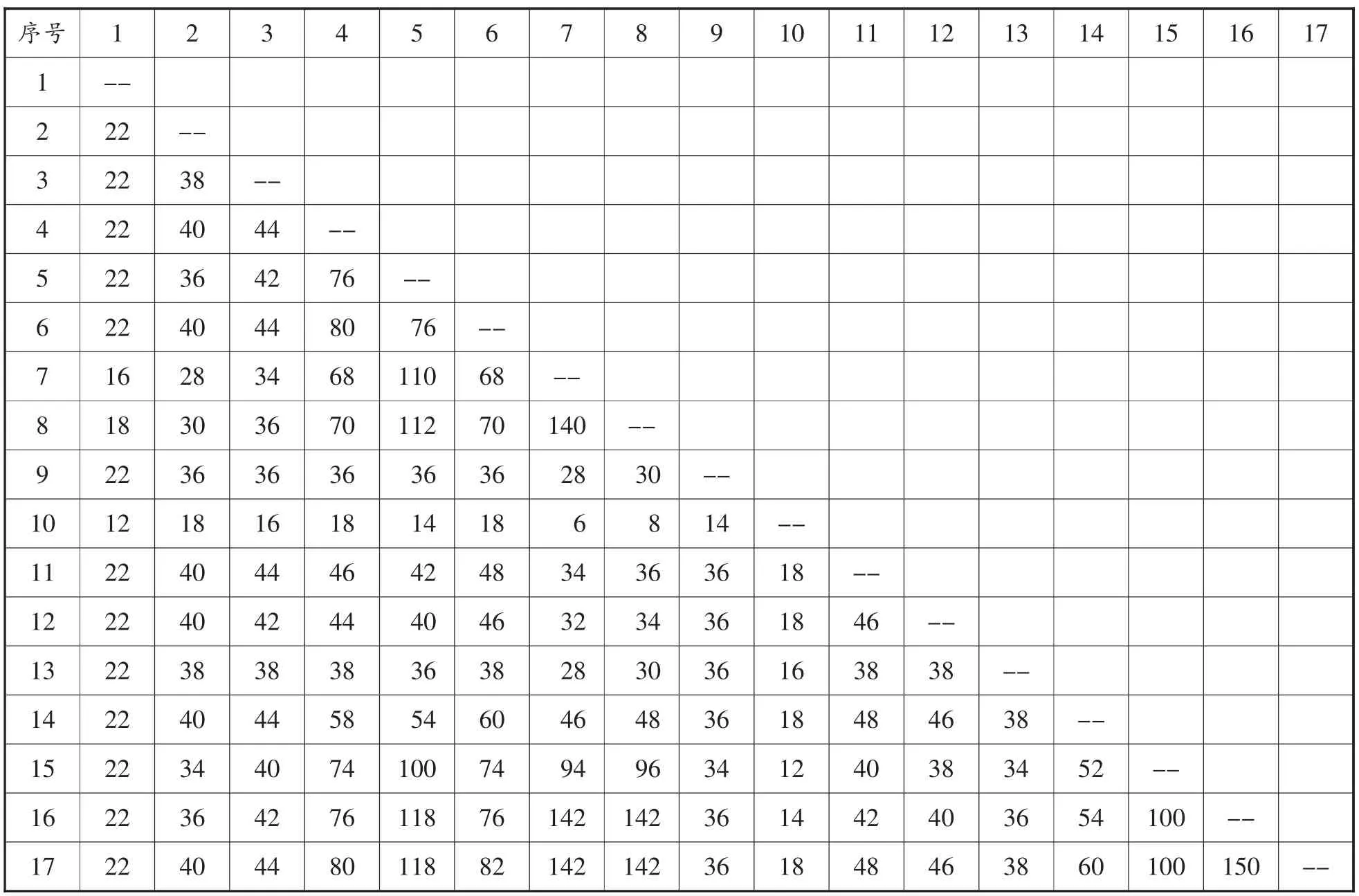
表3 货位组合距离节约值表

3.4 改进节约算法求解

利用改进节约算法进行求解，具体步骤如下。

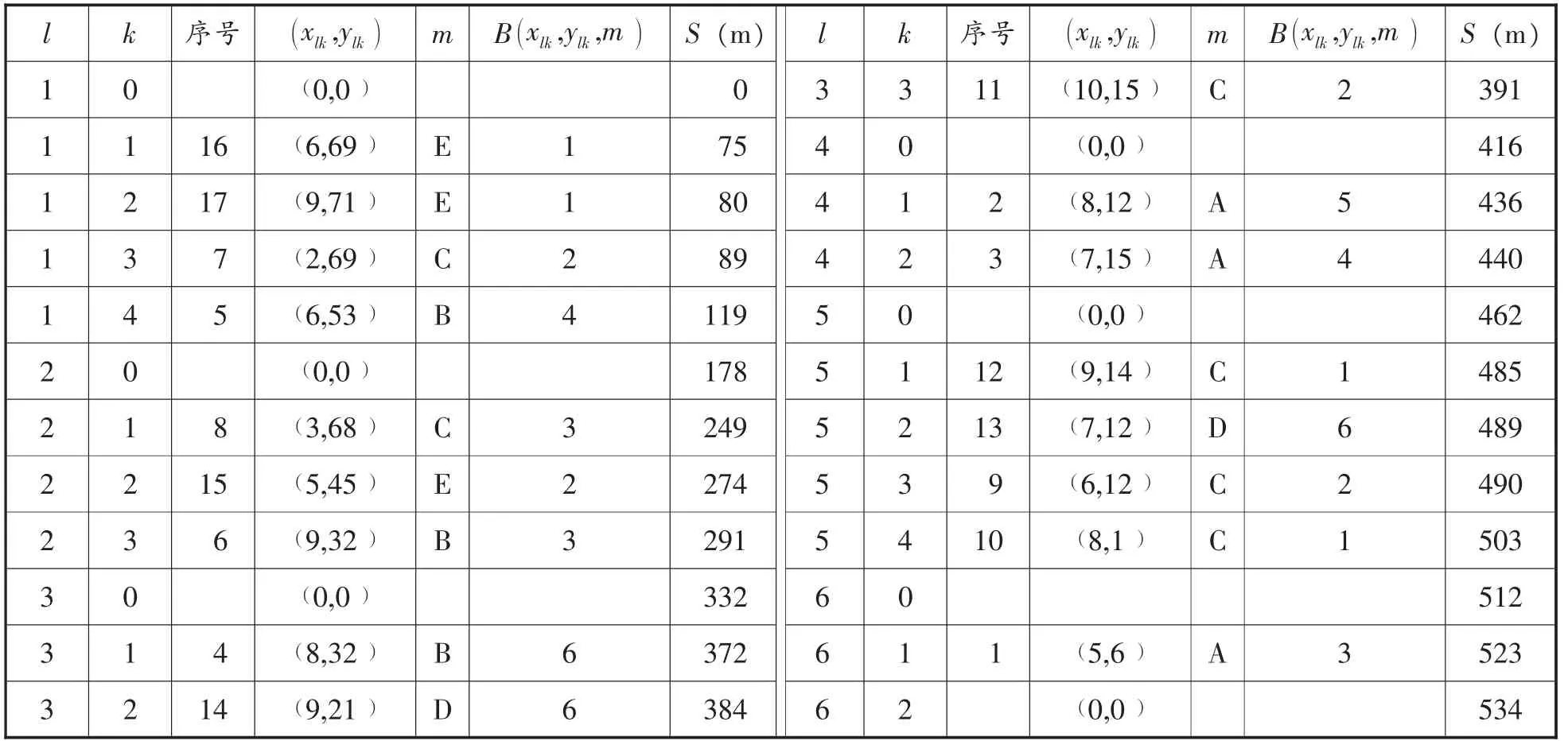
表4 节约算法决策结果

（1）选择节约量最大的16、17货位，器材体积为1×4+1×4=8，拣货箱未装满，在与货位16和货位17有关的组合中查找最大节约量为16、7货位 （或16、8，17、7，17、8），将货位7加入当前拣选序列，此时器材体积为8+2×3=14，拣货箱仍未装满，在货位16、17、7有关的组合中查找最大节约量为16、8货位，将货位8加入当前拣选序列，此时拣货箱只能再拣选货位8内2个器材就装满，巷道车返回巷道口，此时货位8还剩余1个器材等待拣选。这样可以确定第一次拣选的货位 （数量）为7（2 ）、8（2 ）、16（1 ）、17（1 ）。

（2）将已经拣选完成的货位7、16、17从待拣选货位中删除，重复步骤 （1），此时应注意货位8内器材数量为1，应保留与剩余的待拣货位组成新的拣选决策问题，按照 （1）中的步骤进行，直至所有待拣货位全部合并，可以确定第二次拣选的货位 （数量） 为4（5）、5（4）、8（1）、15（2）；第三次为4（1）、6（3）、11（2）、12（1）、13（1）、14（6）；第四次为2（5）、3（4）、13（2）；第五次为1（3）、9（2）、10（1）、13（3）。

经过以上三步分析计算，可得拣选决策结果，如表5所示。

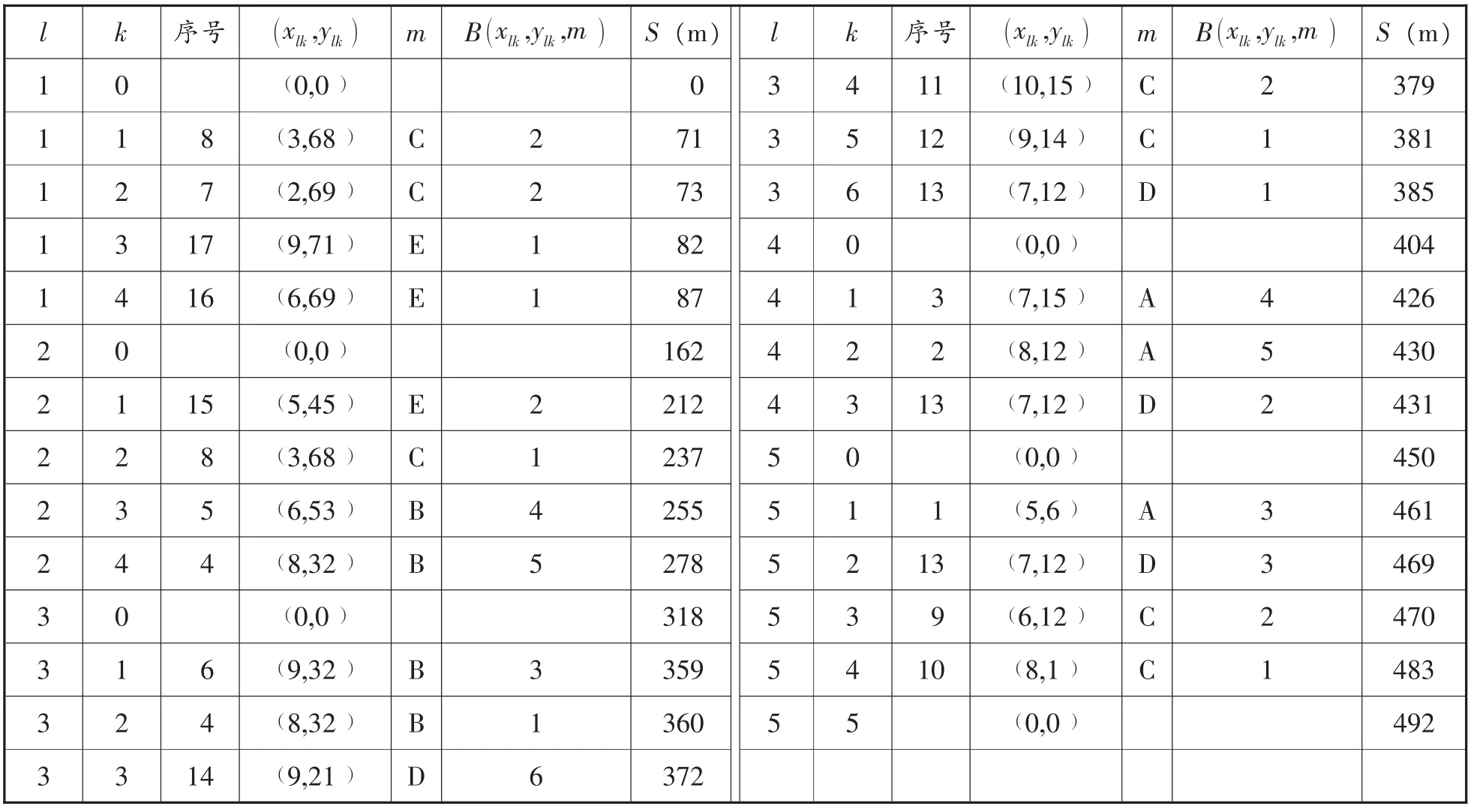
表5 改进节约算法决策结果

3.5 结果分析

由计算结果可以看出，在拣选作业决策上，利用改进节约式算法比传统的节约算法更能减少拣选次数和巷道车的行走距离，说明在拣选作业中利用改进的节约式算法方法是可行和正确的。

4 结 论

本文首先建立了的器材拣选作业的路径优化模型，利用传统节约算法计进行货位拣选的安排决策，分析了传统节约算法用于器材拣选作业中存在的不足，并针对两点不足进行了改进，使得拣选次数更少，拣选行走距离更短，为自动化立体器材仓库的拣选优化问题提供了一种新的思路。

[1] 李诗珍.配送中心拣货作业优化设计与控制研究[D].成都：西南交通大学 （博士学位论文），2008:2－4.

[2] 常发亮，刘増晓，辛征,等.自动化立体仓库拣选作业路径优化问题研究[J].系统工程理论与实践，2007(2):139－143.

[3] 于洁，苏志忠，孙燕飞.蚁群算法在拣货路径优化中的应用研究[J].电脑知识与技术，2008(4):466－467.

[4] 陈一永，许力.C－K节约算法在配载车辆调度问题上的应用研究[J].商场现代化，2009(562):149.