管道输送粉体粒子起电电荷分布实验

孙可平，王树友，王丽芳

(上海海事大学文理学院，上海 200135)

0 引言

对于管道内粉体粒子的静电起电机理，不少学者［1-3]曾用经典的偶电层理论进行解释.偶电层理论确实能解释大多数固体材料的静电起电规律，但粉体粒子兼具固体和流体两相特征，其在管道内的起电涉及大量粒子与管道表面的随机碰撞，起电规律复杂，用偶电层理论解释其起电机理过于简单.为此，本文设计粉体粒子在管道输送过程中的特殊起电模型［4].其要点为:在固体管道内依靠气力输送粉体粒子时，粉体粒子会反复碰撞管道内壁，经历多次摩擦起电，同时又不断释放电荷;当起电量大于释放电荷量时，粉体粒子的电荷量将逐渐增加，最终达到1个平衡值.

虽然单个粒子的起电过程不连续，但大量粉体粒子起电时的电荷转移量可认为是连续的.考虑到起电过程中镜像电荷的影响、已存在空间电荷的影响以及粒子本身电荷的驰豫影响，粒子瞬时电荷量与碰撞次数的1阶导数方程为

式中:qm为粉体粒子单位质量的瞬时电荷量;qm∞为粉体粒子单位质量的平衡电荷量(即最大电荷量);n为单个粒子与管壁的碰撞次数;n0为粉体粒子起电的特征参数.根据初始条件(n=0，qm=qm0)，得

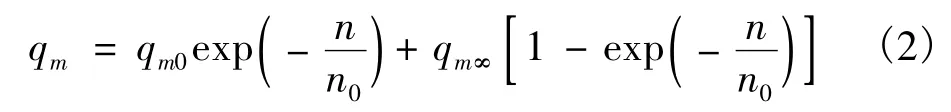
引入1个反映粒子碰撞起电特性的参数——碰撞起电系数k，其定义为

当1个粒子随机与管壁碰撞时，碰撞次数的几率密度函数可用1个二项式分布表示.大量粉体粒子碰撞次数的几率密度函数

当qm0=0且|qm|≪|qm∞|时，即在粒子起电的初始阶段，式(5)可简化为

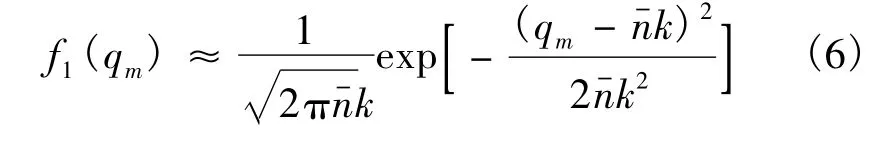
1 实验设备和实验程序

以文献［4]中的“管道输送粉体粒子静电起电新模型”为基础，本文设计1套管道输送中的粉体粒子静电起电电荷分布实验系统，用相关分析仪器进行研究.图1为实验系统示意.实验使用普通粉体粒子，中值直径为7 μm，粒子质量密度为2.3×103kg/m3.为保证实验粒子的连续供应(即在小流量下的粉体粒子也能持续流动)，首先对台式供料器进行改进，使粉体粒子可在空气裹携下进入1个小的虹吸喷嘴.［5]粉体粒子被喷射器扩散后，进入1个内径为4.6 mm的不锈钢直管.直管长度有0.05 m，0.25 m，0.50 m，1.00 m 和2.00 m等5种规格.空气的平均速度范围为36～77 m/s，空气相对湿度约为10%.穿过该直管后，单个粉体粒子的电荷和直径用E-SPRART分析仪(Electrical-Single Particle Aerodynamic Relaxation Time Analyzer)测 量.E-SPRART分析仪是由 MAZUMDER等［6]研制的基于粒子在静电场和声场中的动力学特征的1个测量分析系统.

图1 实验系统示意

2 实验结果

图2为测量得到的粉体粒子穿越整个管道后的电荷分布.

图2 粉体粒子穿越整个管道后的电荷分布

由图2可知，粉体粒子电荷分布很宽，从负到正都有.分布曲线与正态分布曲线类似，左边有个较长的尾部.这条由实验得到的电荷分布曲线形状，与理论计算得出的碰撞起电系数分布图像一致.

图3 管道长度对粒子单位质量电荷平均值的影响

图4 方差与粒子单位质量电荷平均值的相对关系

图5 方差系数与粒子单位质量电荷平均值的相对关系

3 实验结果分析

用式(7)可以对实验数据进行更详细的分析.实验测量和理论计算得到的静电电荷分布见图6.

图6 使用3种实验参数数据得到的电荷分布

图7 粒子与管壁的平均碰撞次数与管道长度的关系

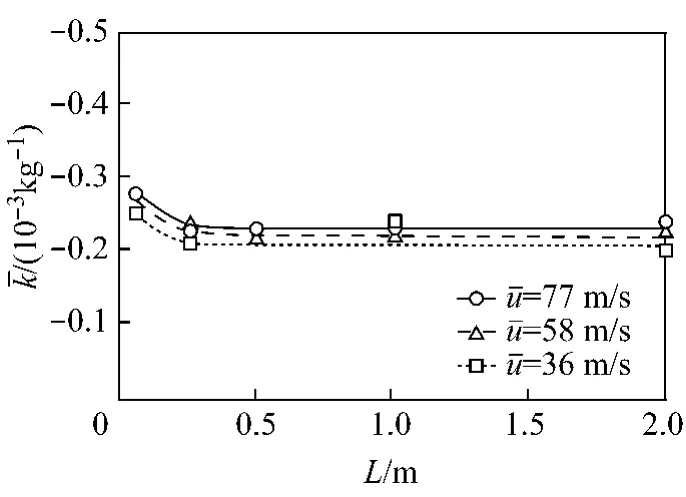
图8 碰撞起电系数平均值与管道长度的关系

碰撞起电系数的标准偏差σk与管道长度的关系曲线见图9.由图可知，σk随管道长度的增加而减少.值得注意的是，碰撞起电系数的平均值随管道长度的增大快速变成常数，其标准偏差却随管道长度的增大而呈斜线下降，与图8显著不同.

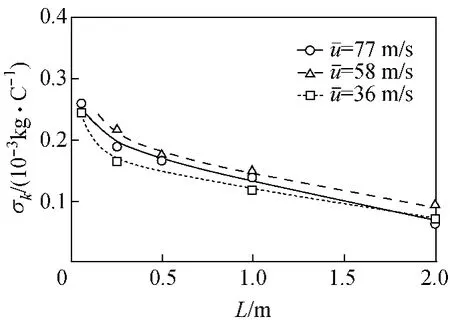
图9 碰撞起电系数的标准偏差与管道长度的关系

5 结论

通过对管道输送粉体粒子起电电荷分布实验的研究，得出以下结论:

(1)粉体粒子电荷从负到正呈广泛分布，说明大量粒子在管道内的起电状况比预想的更复杂.粒子电荷分布实验曲线虽然在电荷极性分布、几率密度极值方面与理论预测有所不同，但分布形态与文献［4]理论分析结果基本一致，说明物理模型基本合理.

［1]LEES P，MCALLISTER D，SMITH J R.An experimental and computational study of electrostatic fields arising during the pumping of powder into small metal and plastic containers［J].IEEE Trans Industry Applications，1985，21(5):1306-1312.

［2]MAURER B.Discharge due to electrostatic charging of particles in large storage silos［J].Germany Chem Eng，1979，4(2):189-195.

［3]孙可平，封根宝.气力输送管道内粉体空间电荷的测量方法［J].上海海运学院学报，1995，16(3):61-67.

［4]于格非，许龙，孙可平.管道输送粉体粒子静电起电新模型研究［J].北京理工大学学报，2009，29(S):71-73.

［5]MASUDA H，MATSUSARA S，SHIMOMURA H.Measurements of powder flow rate in gas-solids pipe flow based on the static electrification of particles［J].Adv Powder Technol，1994，5(3):241-254.

［6]MAZUMDER M K，WARE R E，YOKOYAMA T，et al.Measurement of particles size and electrostatic charge distributions on toners using ESPART analyzer［J].IEEE Trans Industry Applications，1991，27(4):611-619.