倒谱形状规整在噪声鲁棒性语音识别中的应用
杜 俊,戴礼荣,王仁华
(中国科学技术大学电子工程与信息科学系科大讯飞语音实验室,安徽合肥230027)
1 引言
随着自动语音识别(ASR:Automatic Speech Recognition)技术的发展,语音识别器的噪声鲁棒性在实际系统的开发中得到了越来越多的关注。各种各样的噪声鲁棒性技术层出不穷,既有特征域方法也有模型域方法[1-2]。由于模型域方法对运算复杂度要求更高,因此本文中我们关注于特征域方法。在特征域方法中,有一大类称为特征规整方法。首先最简单的是倒谱均值规整(CMN:Cepstral Mean Normalization),CMN虽然简单,但却是一种非常有效的去除时不变信道影响的途径,在很多实际系统中都加以采用;CMN的一个自然扩展是倒谱均值方差规整(MVN:M ean and V ariance Normalization)[3],它通过同时对均值和方差做规整,在达到对信道影响去除的基础上,也能对加性噪声进行很好的抑制。从统计学角度来看,均值和方差分别是和一阶矩和二阶矩相关的,因此自然而然就会想到更为一般化的倒谱高阶矩规整(HOCMN:High Order Cepstral M oment Normalization)[4],实验证明HOCMN确实有更好的噪声鲁棒性。此外,从累积分布函数匹配(Cumu lative Density Function M atching)的角度,有人提出了所谓的双高斯规整(DGN:Double Gaussian Norm alization)[5],DGN方法基于这样一个假设:噪声环境下语音特征分布往往表现出双峰特点。上面这些规整方法都是基于参数化模型,另外还有一类方法是基于非参数化模型的,比如使用累积直方图的直方图均衡(HEQ:H istogram EQualization)[6]。HEQ相比于 CMN和MVN最大的优势在于其非线性变换特性,不仅仅匹配特征分布的均值方差,而是考虑了特征整体分布。针对传统HEQ方法的某些缺陷,又有一系列改进算法,如分数位直方图均衡(Quantile HEQ)[7]、渐进式直方图均衡(Progressive HEQ)[8]和多项式拟合直方图均衡(Polynomial-fitHEQ)[9]。
我们提出的倒谱形状规整(CSN:Cepstral Shape Normalization)方法可以说不仅考虑了以上各种方法存在的缺陷,而且具有更加明确的物理意义。首先CMN和MVN方法本身过于简单,无法对付复杂的噪声环境;HOCMN虽然有所改进,但是其解法并不直接,特别是奇数阶和偶数阶还要分开考虑;HEQ需要较多的数据量来计算累积分布函数,这对于句子级规整来说,总是一个问题。其次,在文献[10-12]中,讨论了语音特征分布的建模问题,并且我们的初步实验表明在噪声环境下语音倒谱特征分布每一维都可以用一般化高斯分布(GGD:Generalized Gaussian Density)来很好的近似。综合以上两方面讨论,提出了CSN方法。它不仅物理意义明确,而且解法也很简单,只需要估计形状因子,对数据量的要求很小。
下面我们将分几部分对CSN方法加以介绍。首先在第二节中,将从原理出发对CSN进行分析和推导;然后在第三节和第四节中,我们将给出实验配置和实验结果,最后在第五节中给出结论。
2 倒谱形状规整(CSN)方法介绍
2.1 语音特征分布分析
在介绍CSN方法之前,我们首先来对噪声环境下的语音特征分布进行初步的分析。在图1中,我们给出了干净环境和噪声环境下各维特征分布的对比,这里的特征我们都做了MVN预处理,因为我们只关心分布形状的变化。我们观察到:在干净环境下,C0维和对数能量维的分布呈现出双峰,而其他维都是单峰的;在噪声环境下(信噪比0dB时),各维分布形状都发生了变化。不过我们发现所有维(包括C0和对数能量)都比较像高斯分布,区别在于不同维分布形状的峰度和偏度不同。
受此启发,我们引入一般化高斯分布(GGD)[12],这里我们用它来很好的拟合噪声环境下的语音特征分布。对于统计信号 x,假设具有零均值和单位方差,那么其一般化高斯分布的概率密度函数如下:
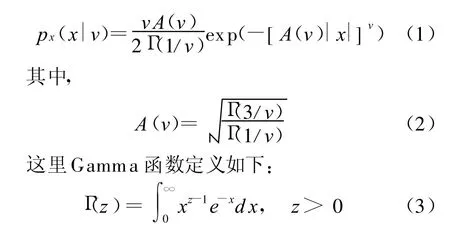
A(v)定义了GGD分布的散度(Dispersion)和尺度(Scale),参数v则描述了指数衰减的速率,一般反映了分布的形状(Shape)或者偏度(Skewness)。图2给出了不同v值对应的概率密度分布图,可以看出,v越小会产生越明显的拖尾和更尖锐的峰。当v=2时,GGD对应于标准高斯或者正态分布。
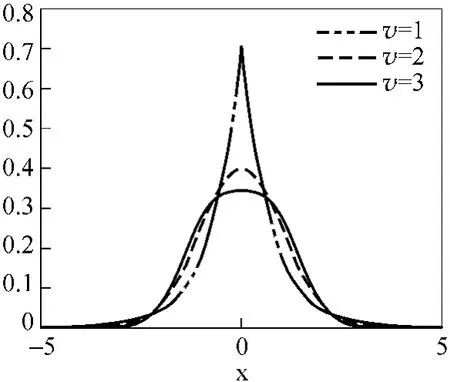
图2 不同v值对应的概率密度函数分布图
2.2 CSN算法描述
基于2.1节的分析,CSN算法可以概述为以下两个步骤(同时对训练和测试数据处理)。步骤1:对倒谱参数进行MVN预处理。
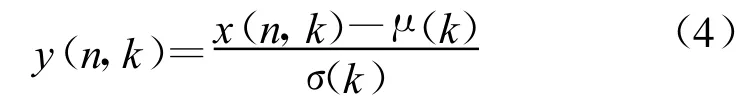
此处x(n,k)表示第n帧原始特征向量的第k维,μ(k)和σ(k)分别表示当前句子第k维特征向量的均值和标准差。
步骤2:利用指数因子进行形状规整。
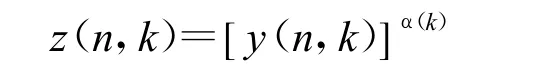
α(k)是第k维形状因子,和GGD分布里面的形状参数v类似。公式(5)中我们的目的就是使得变换之后的特征满足一个由GGD分布表征的参考分布。
为了求出形状因子α(k),这里采用矩匹配估计(MME:Moment M atching Estim ator)[12]。首先我们定义形状参数为v0的GGD分布的r阶绝对中心矩(Absolute CentralM oment):
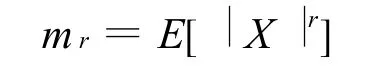
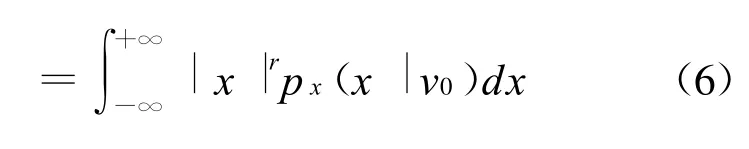
我们把公式(1)带入上式,则可以进一步得到:
接着定义一般化高斯比函数(Generalized Gaussian Ratio Function):

可以看出,公式(8)是根据GGD分布的参数得到的;另一方面,我们利用当前句子本身信息可以得到一般化高斯比函数的估计形式如下:

根据MME准则,我们可以得到形状因子的方程:

很显然,只要求出上述方程的根,就能得到形状因子。可以证明,上式左边函数是关于形状因子的单调函数,因此我们可以采用数值迭代方法快速找到方程的根。最后,我们讨论一下公式(10)中两个自由参数v0和r的确定。我们初步做了一些挑选实验发现当v0=2和r=2时,可以达到最佳性能,其实这组参数具有很强的物理意义。首先,v0=2表示我们采用的参考分布是标准高斯分布;其次,r=2表示公式(7)中我们采用的是统计学里面很重要的物理量—峰度(Kurtosis)。
2.3 特征的时序平滑(Temporal Smoothing)
虽然CSN规整方法能有效地使得测试和训练在统计上达到匹配,但是在某些情况下,由非稳态噪声引起时序上的毛刺,无法通过规整算法进行很好的处理,一般使用一个简单的平滑滤波器解决这个问题,比如本文中采用的ARMA滤波器[13]。
3 实验配置介绍
我们的CSN方法将在aurora2和aurora3两个数据库上加以验证。这两个数据库都是专门为验证噪声鲁棒性算法设计的。Aurora2是人工加噪(包括加性噪声和信道影响)的英文数字串任务,干净数据来源来TIDigits数据库。定义了两种训练方式,一种是干净训练(Clean Condition Training),即训练中只有干净数据;另一种是加噪训练(M u lti Condition Training),即将各种环境下加噪之后的数据混在一起训练,本文实验只采用了干净训练,因为这种情况下测试和训练的不匹配程度最高,能很好的体现规整算法的有效性。测试集按照不同信噪比和噪声环境的组合划分了很多子集,如果按照大类可分为SetA/SetB/SetC三个集合,其中SetA的噪声环境是和加噪训练集完全匹配的,SetB的加性噪声环境和加噪训练集不匹配,而SetC在加性噪声和信道影响两方面都不匹配。
Aurora3也是数字串任务,不过它的数据都是在各种真实的车载环境下采集的,并且包含四种语言:丹麦语、德语、西班牙语和芬兰语。根据测试和训练的匹配程度定义了三种实验模式:高度匹配(Well-Matched)、中度不匹配(M id-M ismatch)、高度不匹配(High-Mismatch)。
实验中我们采用的前端特征包括12维MFCC、C0和对数能量,再加上这些特征对应的一阶和二阶动态扩展特征,其中C0和对数能量每次只选其一。所有的规整方法只对静态特征处理。后端训练和测试部分采用的是aurora任务提供的标准配置,具体可参见文献[14-15]。
4 实验结果与分析
4.1 CSN方法和其它方法对比
这一小节中,我们将CSN方法和四种传统规整方法(MVN,DGN,HEQ,HOCMN)在性能方面进行对比,并且选择对数能量而不是C0。由于M VN是最简单的规整算法,所以可以看成是基线系统,另外HOCMN中奇数阶和偶数阶分别设成3和4。
从表1中可以看出,在aurora2数据库上,CSN方法在不同集合上均表现出最佳性能。并且和MVN相比,总体词错误率有38.0%的相对下降。

表1 Aurora2数据库干净训练方式下CSN方法和其他规整方法在不同测试集上的性能比较
从信噪比的角度,我们在表2中也做了对比。我们发现在高信噪比时,CSN方法和其他方法都可比;而在低信噪比时(5dB以下),CSN要明显好于其他方法。

表2 Aurora2数据库干净训练方式下CSN方法和其他规整方法在不同信噪比时的性能比较
另外,规整算法的有效性还可以通过下面定义的平均距离来度量:
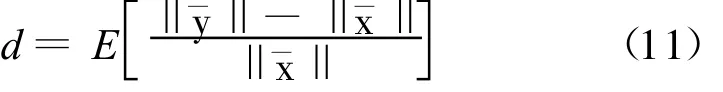

表3 Aurora2数据库CSN方法和其他规整方法关于平均距离度量的比较
下面我们再来看看在aurora3数据库上的对比结果。如表4所示,CSN方法在三种模式下(高度匹配、中度不匹配和高度不匹配)的平均性能都取得了最好性能,特别是在高度不匹配的时候更为明显。并且和M VN相比,总体词错误率有25%的相对下降。另外,从不同语言来看,CSN在绝大多数时候也都是最佳。如果对比表1和表4,我们发现传统方法如 DGN、HEQ、HOCMN,在 aurora2和 aurora3两个数据库上的性能排序并不完全一致,这也说明了我们的CSN方法在不同数据库上的表现更加稳定。
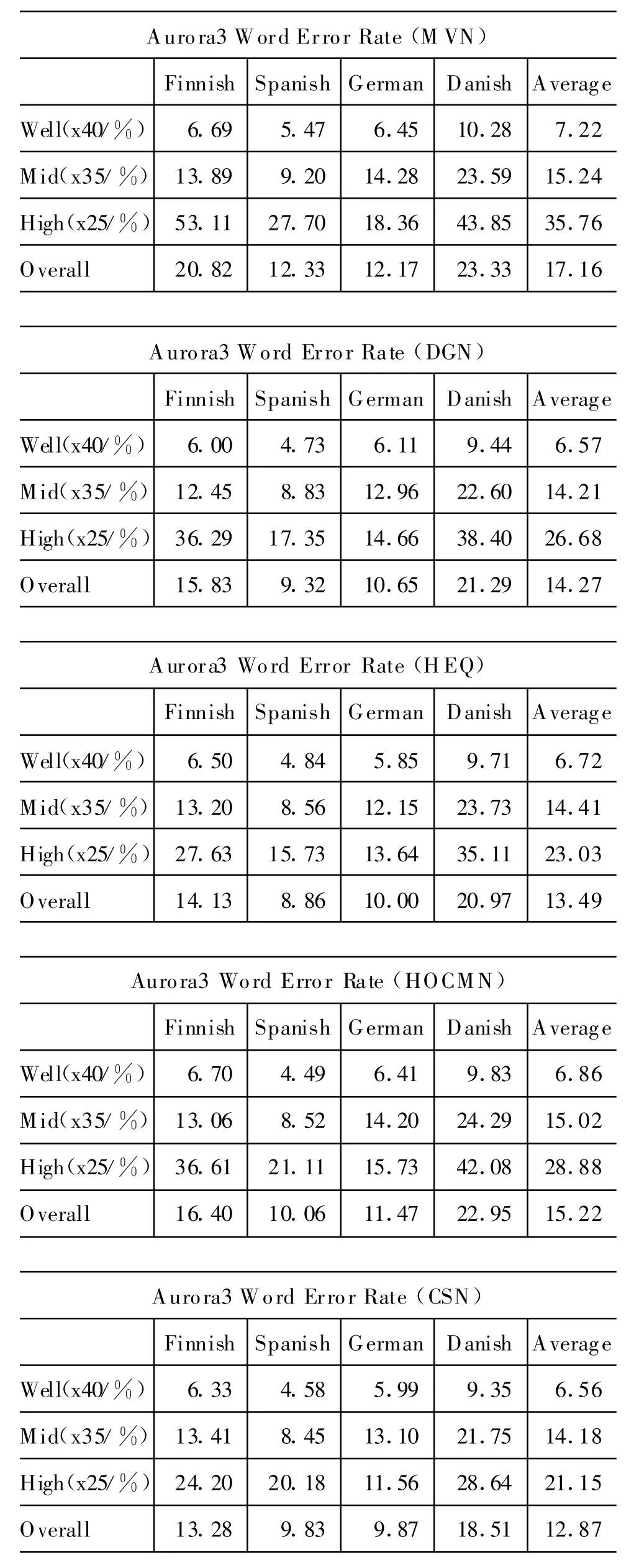
表4 Aurora3数据库CSN方法和其它规整方法的性能比较
4.2 考虑各种改进的CSN方法
为了得到进一步的性能提升,考虑将下面几种技术和CSN结合在一起使用:1)采用C0代替对数能量,有实验室表明C0在噪声环境下更加鲁棒;2)之前提到的规整算法都是基于句子级,其实当句子很长时,有时采用分段规整效果会更好,即对于当前帧,左右各取L/2帧组成一段数据,再计算各种统计量,我们发现段规整在aurora2上有效果,但aurora3上效果并不明显;3)加入M阶的ARMA平滑滤波器。

图3 Aurora2数据库各种技术和CSN结合后的性能比较
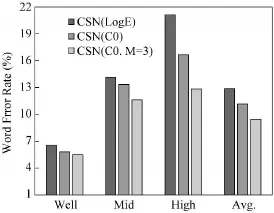
图4 Aurora3数据库各种技术和CSN结合后的性能比较
各种改进之后的性能对比如图3和图4所示。图中,LogE表示未做任何改进的CSN,C0表示用C0替换LogE,L表示采用长度为L的段级规整,M表示使用M阶ARMA滤波器。可见改进后效果比较明显,相比于未做任何改进的CSN,最好性能在aurora2和aurora3两个库上分别带来词错误率18.9%和26.4%的相对下降。
5 结论与展望
本文中提出的CSN规整算法,直接对特征分布的形状进行规整,实验证明非常有效,比MVN方法好了很多,相比其他传统方法也是一致变好。并且通过一些对CSN的简单改进,进一步带来了提升。在将来的工作中,我们会考虑将CSN算法和其它鲁棒性技术进一步结合,以期带来更好的性能。
[1] 丁沛,曹志刚.基于语音增强失真补偿的抗噪声语音识别技术[J].中文信息学报,2004,18(5):64-69.
[2] Y.Gong.Speech Recognition in Noisy Environments:A Survey[J].Speech Communication,1995,16(3):261-291.
[3] O.V iikki and K.Laurila.Cepstral Domain Segmental Feature Vector Normalization for Noise Robust Speech Recognition[J].Speech Communication,1998,25(1):133-147.
[4] C.-W.Hsu and L.-S.Lee.Higher Order Cepstral M oment Normalization(HOCMN)for Robust Speech Recognition[C]//IEEE Proc.of ICASSP,2004:197-200.
[5] B.Liu,L.-R.Dai,J.-Y.Li and R.-H.Wang.Double Gaussian Based Feature Normalization for Robust Speech Recognition[C]//Proc.of ISCSLP,2004,253-256.
[6] A.de la Torre,J.C.Segura,C.Benitez,A.M.Peinado and A.J.Rubio.Non-linear Transformations of the Feature Space for Robust Speech Recognition[C]//IEEE Proc.of ICASSP,2002:401-404.
[7] F.Hilger and H.Ney.Quantile Based H istogram E-qualization for Noise Robust Speech Recognition[C]//Proc.of EUROSPEECH,2001:1135-1138.
[8] S.-N.Tsai and L.-S.Lee.A New Feature Extraction Front-End for Robust Speech Recognition using Progressive H istogram Equalization and Mu lti-Eigenvector Temporal Filtering[C]//Proc.of ICSLP,2004:165-168.
[9] S.-H.Lin,Y.-M.Yeh and B.Chen.Exp loiting Polynom ial-fit H istogram Equalization and Temporal Average for Robust Speech Recognition[C]//Proc.of ICSLP,2006,2522-2525.
[10] S.Gazor and W.Zhang.Speech Probability Distribution[J].IEEE Signal Processing Letters,2003,10(7):204-207.
[11] J.W.Shin,J.-H.Chang and N.S.K im.Statistical M odeling o f Speech Signals Based on Generalized Gamma Distribution[J].IEEE Signal Processing Letters,2005,12(3):258-261.
[12] K.Kokkinakis and A.K.Nandi.Speech Modelling Based on Generalized Gaussian Probability Density Functions[C]//IEEE Proc.of ICASSP,2005:381-384.
[13] C.-P.Chen,J.Bilmes and K.K irchhoff.Low-Resource Noise-robust Feature Post-processing on Aurora2.0[C]//Proc.of ICSLP,2002:2445-2448.
[14] H.G.H irsch and D.Pearce.The AURORA Experimental Framework for the Performance Evaluations of Speech Recognition Systems under Noisy Conditions[C]//Proc.of ISCA ITRW ASR,2000:181-188.
[15] A.M oreno,et al.SpeechDat-Car:A Large Speech Database for Automotive Environments[C]//Proc.of LREC,2000:373-378.

