灰预测模式评估观光农业之游客量

梁大庆,张俊斌

(1.台湾虎尾科技大学,台湾 云林 63201;2.台湾中州科技大学,台湾 彰化 51450)

1 前 言

时代的潮流与变迁,农业产业的转型成了解决农业产业问题的重要方向。休闲农业将农村资源提供观光游憩使用,以提高农民的所得与福祉,并增加游憩资源的供给,以满足游客的需求。台湾休闲农业的推展有两个方向:其一为农业生产结构的提振,其二为休闲游憩机会的提供。为满足休闲活动需求的增加与多样化的要求等多方面考虑,于1993年起实施 “休闲农业区设置管理办法”,随着1996年 “休闲农业辅导办法”的修正完成,休闲农业的推动也有显著之发展。近年台湾地区政治与经济环境产生颇大的变化,所面对的环境亦不断的变迁,相关的产业亦不断地改变。以观光旅游产业为例,餐饮、旅馆、航空、运输、旅行业等多项产业过去都是观光产业的主干,而农业观光休闲产业已被认为是未来发展的优先选择[1],振兴观光还有助于活络关联产业。酒产业与酒文化向来与日常生活习习相关,在台湾酒产业渐渐地影响地方生活文化,可说是带动观光产业的火车头。南投埔里酒厂是台湾的酒乡,现已转型为休闲观光酒厂,设有酒文化馆及产品展示中心,并结合当地观光资源共同推展文化活动,以 “文化酿酒、艺术观光”为主轴,配合邻近观光游憩景点,孕育旅游空间,活络埔里的酒文化观光特色,以吸引更多的观光客到埔里來旅游和消费,埔里酒厂不仅是生产制造者,也是文化历史保存者,更是观光发展的推手[2]。虽自921震灾重创后,使得南投地区观光一落千丈,如今埔里酒厂为埔里地区观光产业的重点区域,因此以埔里酒厂为例进行分析,实具有指标性之意义。

目前关于观光旅游产业之预测,多半是透过单变量与多变量之解释变量来建立预测模型。但传统计量经济学及统计分析需要庞大样本数据作为建模的基础,且必须符合统计上的相关检定,才会有较佳的预测精确度;相较于灰色系统理论是针对系统模型之不确定性及信息之不完整性下,只需少量数据便可建立预测模型,灰色系统理论更为简便[3]。因应科技时代的快速变化,以往需要收集大量数据样本才能预测长期规律的预测模型,在现实环境中较没效率;反而是样本数据比较少,计算过程简单,较具时效性的灰色预测模型渐渐地被广泛应用于各领域中。H sing et al.将灰色理论应用于职灾类型的分析与预测[4];Chen et al.应用灰预测理论预测台湾3G行动电话市场[5];余尚武等应用动量权重及灰预测傅立叶残差修正模型于台湾股票市场电子股之投资组合策略[6];Wang使用模糊时间序列与灰色马可夫修正预测模型来预测观光需求,证实灰马可夫修正预测模型能改善GM(1,1)预测模型对于数据随机波动性较大之缺点[3]。本研究应用GM(1,1)、滚动检验、灰色马可夫以及灰色傅立叶级数残差修正预测模型来预测埔里酒厂游客量,并对它们进行比较与分析,总结各预测模型对所选择数据型态的适性,以提供未来游客量评估之参考依据。

2 基地概况

秉承 “文化酿酒、艺术观光”的传承与经营理念,埔里酒厂营造 “绍兴故乡”在埔里生根发展,不仅已经是属于地方的一个活的产业文化,更已成为一个具有酒历史内容的产业体,且具指标性意义的重点游憩产业。

2.1 区域地理位置

酒厂位处台湾南投县埔里镇内,其位置如图1、图2。而埔里镇位居南投县北部,东与东北面临接仁爱乡,南临鱼池乡,西与西北面接国姓乡,以埔里是皆为中心,西距草屯镇41 km,西北距台中61 km,东距雾社23 km,南距日月潭17 km,如图3。

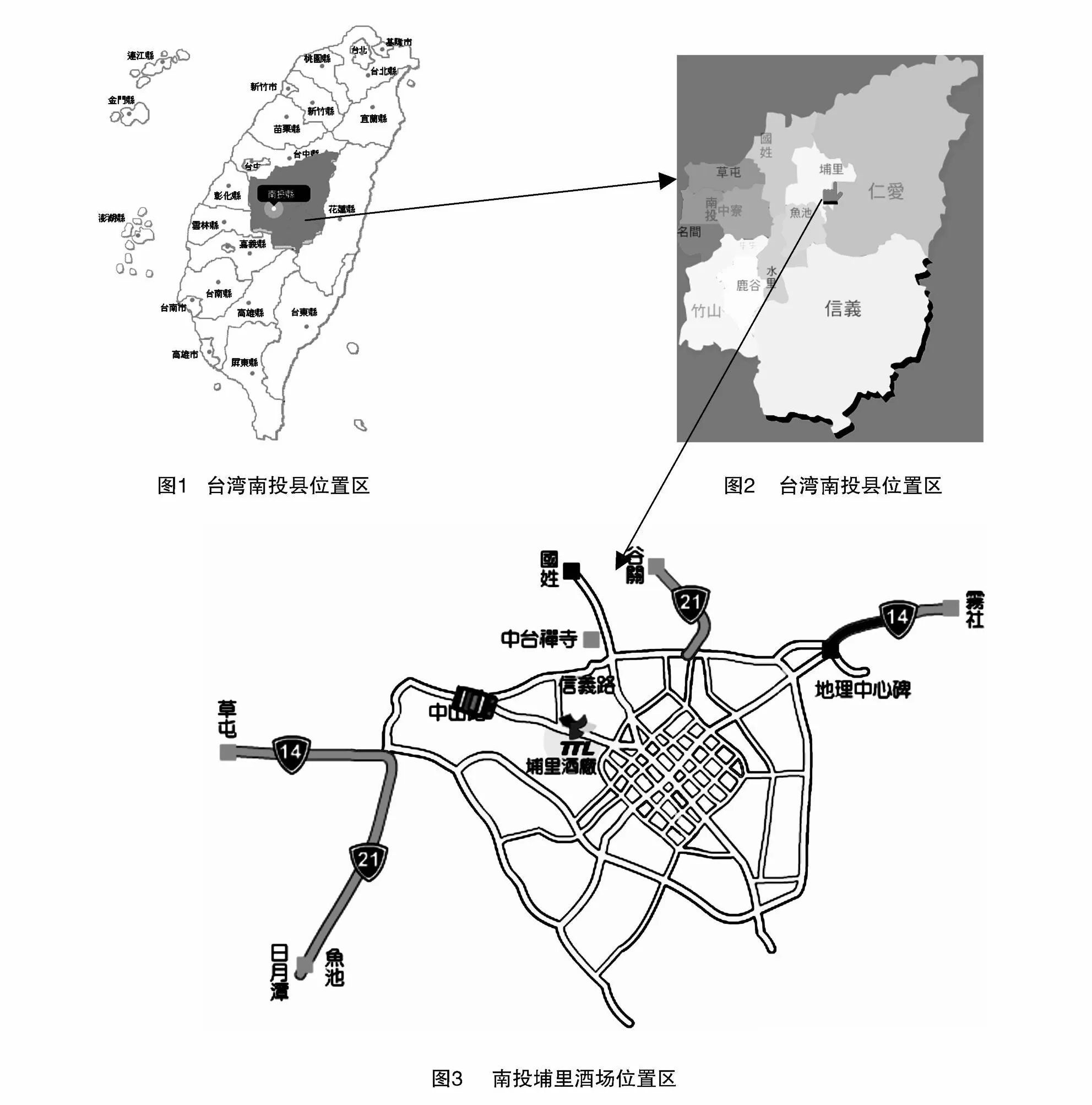
2.2 产业特色

埔里酒厂成立于1902年日据大正年间,其前身为埔里社制酒株式会社,大正11年日人禁止民间制酒,台湾总督府专卖局于这一年的6月30日接收,改名为埔里出张所,台湾光复后,埔里酒场由省政府烟酒公卖局管辖,这时的埔里酒厂只生产米酒、太白酒、糯米酒,而且生产不多,后来才改以生产绍兴酒为主。埔里酒厂生产的绍兴酒,之所以香醇芬芳广受酒客欢迎,原因之一是拜埔里水质甘良之所赐,酒厂生产酒的水来自爱兰台地的泉水,近几年来埔里酒厂除了积极推出爱兰白酒、爱兰喜酒、吟酿清酒等新酒之外,同时还大力推动观光,设立酒文化馆,举办酒文化活动,为酒厂的发展找到新的契机,目前酒厂已成为埔里地区最热门的一个观光景点。藉由 “产业文化化、文化产业化”的策略,并且结合地方艺文,观光资源,为国内 “观光酒厂”经营休闲游憩方向经营成功的案例。

3 研究方法

灰预测理论属于灰色系统理论的研究内容之一,该理论是由邓聚龙教授于1982年所提出,主要是针对系统模型之不明确性及信息之不完整性之下,进行关于系统的关联分析及模型建构,并借着预测及决策的方法来探讨及了解系统的情况。并能对事物的不确定性、多变量输入、离散的数据及数据的不完整性做有效的处理。其中灰预测即是以GM(1,1)模型为基础,对现有数据所进行预测的预测方法,找出某一数列间各个元素之未来动态状况,不需要太多数据,且数学基础较简单[7]。

3.1 灰预测GM(1,1)模型

灰预测理论的基础是针对系统过去已发生之数据序列,透过累加生成进行数据处理,以提供建模之中间讯息,弱化原始数列的随机性,从而发现、揭示潜在的规律,并由规律中预测未来可能的情况[1]。

滚动检验 (Rolling Checking)是利用同一序列前面几个数据 (通常为4笔)来建立GM(1,1)模型,预测下一个数据后,再舍弃原始序列中第1笔数据,加入第5笔数据建立GM(1,1)模型,预测第6笔数据,依此类推的做到原始数据的最后一笔数据为止[7]。由于滚动检验法是基于新讯息优于旧讯息的观点,调整序列发展趋势的变化度,因此对趋势发展变化较为强烈的数据更能显示预测的精确度。

3.2 灰色马可夫预测模型

灰色马可夫预测模型M arkov GM(1,1),是由田自力与刘碧发于1996年提出,认为GM(1,1)预测模型适用于数据数据少且符合所谓 “广义能量系统”的预测,只需少量的数据 (超过4个)即可建立预测模型;但其拟合函数只是一条平滑的指数函数曲线,对于趋势变动较大的数据拟合较差,预测精确度也较低,故将GM(1,1)预测模型与马可夫转移矩阵预测的优点相结合,充分利用历史数据给予的信息,提高数据随机波动性较大之预测精确度,且适于长期预测,有效的提升GM(1,1)预测模型对于此类数据的预测精确度[8]。

3.3 灰色傅立叶级数残差修正预测模型

傅立叶残差修正方法分为傅立叶级数残差修正法、傅立叶余弦级数残差修正法及傅立叶正弦级数残差修正法,本研究将以GM(1,1)傅立叶级数残差修正预测模型来预测游客量,透过傅立叶函数适用于周期性系统表达之特性,以改善GM(1,1)预测模型做一次累加生成后的指数函数图形常会因为社会环境的变迁、循环,而在不同时期有不同的指数率,造成此类大趋势之周期性数据预测精确度较差。

3.4 残差检验

利用建模所得到的预测数据和原始数据间做残差比较,以了解实际值和预测值间之误差及模型精确度。

4 实证研究与分析

由于游客量的变化对于观光旅游业者之经营管理具有决策性的影响,因此本研究整理统计南投埔里酒厂2008年1月至2009年3月之游客量,如表1所示。首先探讨游客量之变化情形,再利用GM(1,1)、滚动检验、灰色马可夫以及灰色傅立叶级数残差修正方法建立预测模型,对它们进行比较、分析,并预测2009年4月之游客人次。

4.1 游客量变化之探讨

由图4之结果可知,埔里酒厂每月游客量平均在15万人次以上;而7月、8月暑假期间,学生旅游族群较多时期,游客量突破20万人次,但相对于9月学生开学时期,其游客量由20万人次骤降只剩10万人次,惟至此后游客量均达15万人次以上,显见埔里酒厂确实拥有相当高的观光游憩潜力。

表1 埔里酒厂游客量统计表

4.2 预测结果之探讨

在观光旅游市场中有很多未知的讯息,例如:气候、景气、流感疫情等因素,使得观光旅游地区之游客人次具有不确定性、波动性及周期性等特征,故本研究应用前述研究方法建立预测模型,据以预测游客之数量。

4.2.1 GM(1,1)模式 以南投埔里酒厂统计2008年1月至2009年3月之游客量,建立原始数列(165 625,169 179,167 931,166 036),再由3.1节所介绍之GM(1,1)公式求得预测值 ,其预测结果如表2所示。由表2可知,最大残差值为48.11%,最小残差值为 0.06%,平均残差值为10.50%,最佳模型精确度为99.94%,最差模型精确度为51.89%,平均精确度为89.50%,显示预测模型预测效果在可接受的水平内。

4.2.2 滚动检验 本研究利用滚动检验法新讯息优于旧讯息的特性,且对于趋势发展变化较为强烈的数据有较高的精确度,建立预测模型,即以(165 625,169 179,167 931,166 036)预测2008年5月之游客量;以 (169 179,167 931,166 036,169 479)预测2008年6月之游客量;以(167 931,166 036,169 479,152 581)预测2008年7月之游客量,以此类推的做到原始数据的最后一笔数据为止。由表3预测结果得知,最小残差值为2.97%,最大残差值为101.94%,平均残差值为25.68%。然而,造成2008年9月实际值与预测值间之误差过大的主要原因,是因滚动检验法以新信息取代旧信息,因而无法反应过去旧信息之波动性及周期性之变化,以致无法精确预测游客量,故滚动检验法较不适合此类具波动性及周期性数据型态之预测。

表2 GM(1,1)之预测结果

表3 滚动检验之预测结果

4.2.3 灰色马可夫 GM(1,1)预测模型能展现预测序列的发展变化总趋势,且只需少量数据(4笔以上)即可建模预测;但其拟合函数只是一条平滑的指数函数曲线,对于随机性较大的数据拟合较差,预测精确度也较低,而马可夫链则适用数据随机性较大的预测,并可用来确定状态的转移概率。在进行灰色马可夫预测模型时,首先要建立灰预测GM(1,1)模型,再加入马可夫过程,而输入变量是依据最小平均残差值所选出的最适建模点数和状态参考数据笔数,因而Grey M arkov的所有相关参数设定如表4所示。

表4 灰色马可夫参数设定表

由Grey Markov预测模式所求得的预测值与实际值间的残差均明显偏低,平均残差值为3.53%,预测模型之平均精确度高达96.47%,显示预测模型之准确度相当高,如表5所示。

4.2.4 灰色傅立叶级数残差修正预测模型当GM(1,1)预测模型之原始序列经过累加生成后,会出现明显的指数规律,但实际系统发展时会受各种因素影响,不可能以某一定速度发展,而是不同时期有不同的指数率发展。因此本研究利用傅立叶函数适用于周期性系统表达之特性,依据GM(1,1)建模方法求出预测值X(0)(j),并将预测值和实际值做残差比较,得到残差序列E(j)(108,-222,110,-4 881,104 83,-44 066,-60 978,51 498,6 695,-5 890,-818,-19 120,-5 944,-29370,-53 283),再利用傅立叶级数作残差修正,得到修正后残差Ea(j),预测结果如表6所示。由表6得知,最大残差值为4.29%,最小残差值为0.58%,其平均精确度高达97.66%。

表5 灰色马可夫之预测结果

4.2.5 各预测模型之比较 由表7及图4研究结果显示,滚动检验法之预测精度较差,其平均残差值为25.68%,平均精确度为74.32%。灰色马可夫及灰色傅立叶级数残差修正预测模型之预测精确度均高达95%以上,显见灰色马可夫及灰色傅立叶级数残差修正预测模型皆适合此类观光旅游需求之预测,唯透过此两种预测模型预测2009年4月游客量与埔里酒厂于2009年5月所公布的游客量统计资料相比时,灰色马可夫预测之游客量为148 487人次,其残差值为26.41%,而灰色傅立叶级数残差修正预测模型之游客量为197 559人次,其残差值为2.09%,显然灰色傅立叶级数残差修正预测模型之预测较为精准,且较灰色马可夫预测模型更适于此类具波动、周期性质的数据型态之预测。

表6 灰色傅立叶预测结果

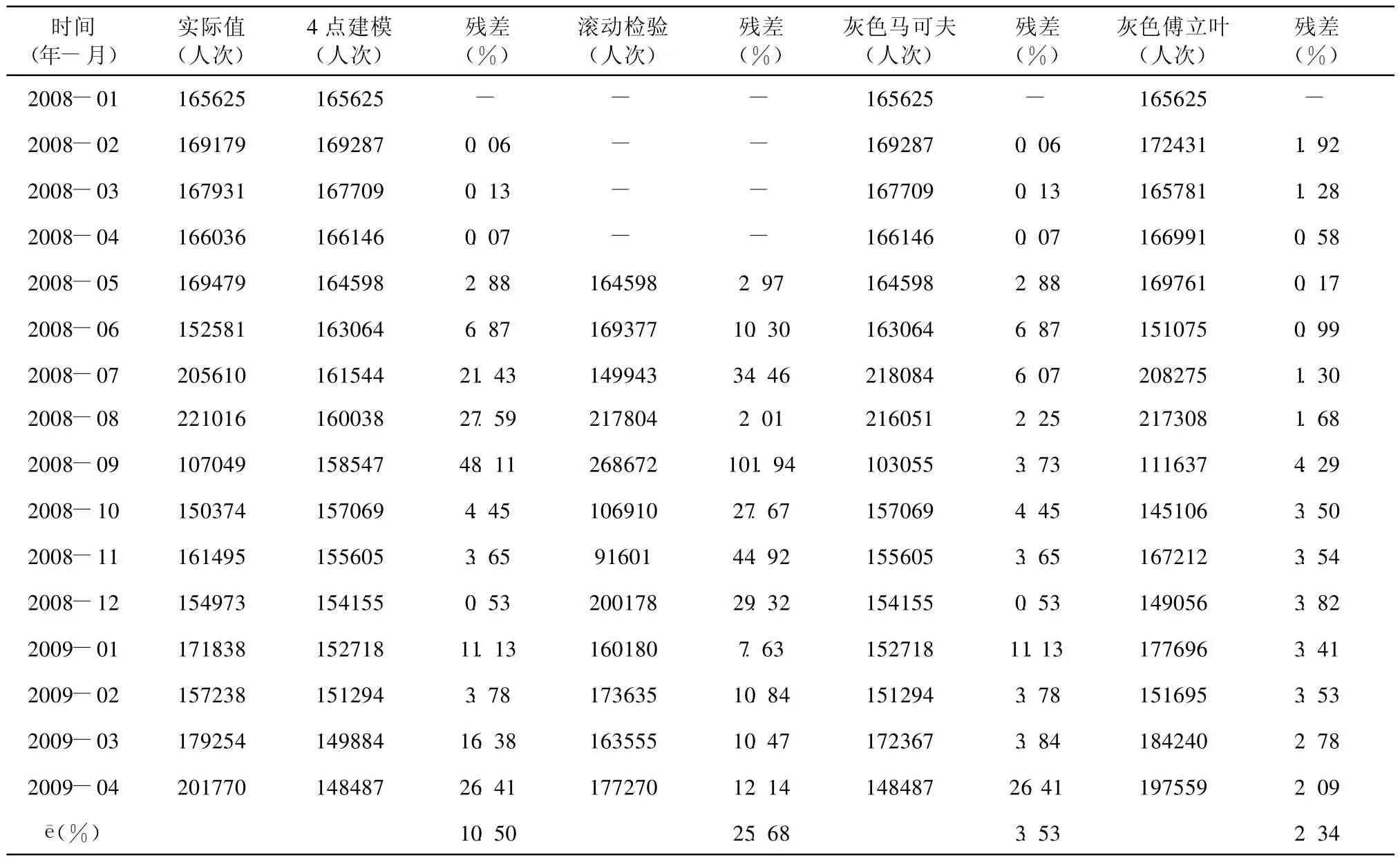
表7 各预测模型之比较及2009-04之预测值

图4 预测模型之比较

5 结论与建议

以灰预测少量数据的特性,采用GM(1,1)、滚动检验、灰色马可夫以及灰色傅立叶级数残差修正预测模型建构游客量预测模型,并以2008年1月至2009年3月南投埔里酒厂游客量统计资料为建模样本进行预测分析。研究结果显示,灰色马可夫及灰色傅立叶级数残差修正预测模型均适合此类观光旅游需求之预测,其中灰色傅立叶级数残差修正预测模型之预测精确度高达97.66%,主要是因游客量之趋势变化受到旅游地点、交通路线、旅游潮流、气候因素、景气因素、流感疫情等影响,而具有周期波动的特性,因此使用具周期波动性质的预测模型最为适合。然而马可夫之长期预测及数据随机波动较大的特性与傅立叶函数适用于周期性系统表达之特性,恰可以弥补灰色预测的局限。

此外,灰色马可夫及灰色傅立叶级数残差修正预测模型皆需使用较多的历史数据才会有较佳的预测精度,才能反映其长期的整体趋势及周期性质,进而订定更精确、更完善的计划及投资策略,相对必须花费较多数据搜集的时间成本与前置成本。希望本研究建立之埔里酒厂游客量预测模型能提供后续研究者针对相关议题之参考,以及提供相关单位、地方政府与民间企业之相关策划部门,做为对未来农业休闲观光需求政策方针之拟订与观光市场营销、营运策略之参考。

[1]高俊雄译.观光旅游地区发展[M].台北︰桂鲁有限公司,1998.

[2]黄跃雯,黄亦锡,叶碧华,等.酒类观光对地方区域发展冲击之研究 [J].观光研究学报,2003,10(1):1-19.

[3]Wang C H.Predicting tourism demand using fuzzy time series and hybrid g rey theory[J].Tou rism Managem ent,2004,25(3):367-374.

[4]Hsing C Y,Chang Y C,Yang CC,et al.An assessment of occupational accident impact factors using the grey system[J].Jou rnal of Occupational Safety and Health,2004(14):58-68.

[5]Chen H S,Yan T M,Kung C Y.A pplication of grey prediction theory to forecast 3G mobile phone in Taiw anese market[J].Journal of Grey System,2008,11(1):43-48.

[6]余尚武,卢瑞山,林盈成.应用动量权重及灰预测傅立叶残差修正模型于台湾股票市场电子股之投资组合策略[J].电子商务学报,2009,11(1):259-286.

[7]温坤礼,黄宜丰,陈繁,等.灰预测原理与应用[M].台北:全华科技图书公司,2002.

[8]田自力,刘碧发.灰色马尔可夫链预测模型 [C]//台湾第一届灰色系统理论与应用研讨会.1996:157-161.