基于桩-土相互作用的内河架空直立式码头地震响应分析

周世良，吴飞桥，李 怡

（1.重庆交通大学河海学院，重庆400074；2.长江航运规划设计院，武汉430030）

随着内河航运事业的发展，内河架空直立式码头结构正被越来越多的应用于内河码头中，成为内河集装箱码头中最重要的结构型式。与此同时，三峡库区的蓄水增加了库区诱发地震的可能性，为了保证码头结构在地震荷载作用下能够安全工作，对其抗震性能进行全面的研究是十分必要的。现有的研究中，其计算模型都是将桩基础在嵌固点处截断并假设为弹性嵌固，不考虑桩土相互作用对结构抗震的影响。这样的处理方法在土体覆盖层较薄的地区是合理的，不仅结构的计算方便，而且能满足工程要求。但在土体覆盖层较厚的地区，桩土相互作用是一个不可忽略的因素［1-3］，如果仍采用上述处理方法就会与实际情况不符，导致计算结果存在偏差。本文结合实际工程，采用有限元法，分别建立桩-土-码头结构模型和不考虑桩土相互作用的2种码头结构计算模型，通过模态分析和动力时程分析，研究不同的计算模型对码头岸坡土体覆盖层较厚地区内河架空直立式码头抗震性能的影响。

1 理论依据

1.1 有限元法的基本步骤［4］

（1）连续体的离散化。

结构的离散化是将被分析的结构用选定的单元划分为有限单元体，把单元的一些指定点作为单元的结点，以单元的集合来代替原结构。

（2）位移模式的选择。

将单元中任一点位移用节点位移与坐标函数来表示，该坐标函数称为位移模式或位移函数

式中：｛f｝为单元内任一点的位移矩阵；［N］为单元的形函数矩阵；｛δ｝为单元节点位移矩阵。

（3）单元刚度矩阵。

利用虚位移或最小势能原理建立单元刚度方程

式中：｛F｝e为等效节点力列阵；［k］e为单元刚度矩阵；｛δ｝e为单元节点位移矩阵。

（4）总体刚度矩阵。

对单元进行组装建立结构的刚度方程

式中：［k］为整体刚度矩阵；｛δ｝为整个结构体的结点位移列阵；｛F ｝为荷载列阵。

（5）求解方程组。

对整体刚度方程进行求解，计算出各结点位移，再利用以上几个方程，可计算出各单元任一点的位移、应变及应力。

1.2 动力方程及求解［5］

桩-土-码头结构体系在地震动作用下任意时刻t的运动方程为

采用混合法求解式（4），将荷载划分为多个荷载步，每个荷载步采用牛顿-拉普森法求解，而每个迭代子步采用Newmark法计算。

2 模型的建立

2.1 计算参数

取寸滩港一期工程的码头结构作为内河架空直立式码头的一般型式，桩基和上部结构为现浇混凝土结构，采用线弹性本构模型，弹性模量为30 GPa，泊松比为0.167，密度为2 500 kg/m3；岸坡覆盖层土体采用Drucker-Prager弹塑性本构模型，其土体参数和弹塑性本构关系见表1。

表1 岸坡覆盖层土体参数Tab.1 Soil parameters for solpe overburden

2.2 边界条件与网格划分

分别建立桩-土-码头结构体系模型（模型Ⅰ）、地基刚性假定的码头结构模型（模型Ⅱ）以及工程计算简化的码头结构模型［6］（模型Ⅲ）（图1）。模型Ⅱ的桩基在土层表面处弹性嵌固，通过与模型Ⅰ的对比分析，研究桩土相互作用对码头结构抗震性能的影响；模型Ⅲ是工程中框架码头结构计算常采用的计算模型，其桩基在弹性嵌固点处嵌固，通过与模型Ⅰ的对比分析，研究与桩-土-码头结构模型相比所产生的偏差。码头结构采用梁单元，岸坡土体采用平面应变单元，由于2种单元间的自由度不对应，故需用约束方程约束rz方向的自由度。模型Ⅰ在岸坡土体底部固定，为了消除有限元边界对地震波的影响，土体两侧采用粘弹性边界；模型Ⅱ、Ⅲ在嵌固点处固定。

图1 码头地震响应分析有限元模型Fig.1 Finite element models for the seismic response analysis of the wharf

2.3 计算荷载及其输入

为了准确模拟地震发生时的实际情况，并满足弹塑性动力时程分析的要求，将同时考虑地震荷载和结构自重。由于采用的码头岸坡属于Ⅱ类场地，故选用El-Centro和Taft地震波，按抗震设防烈度的要求，调整加速度峰值后输入。桩-土-码头结构体系计算模型，采用土层底部输入地震波，而地基刚性假定下的码头结构模型则是采用桩基底部输入地震波，其中地基刚性假定模型输入的地震波是将桩-土-结构计算模型中的地震波在该模型土体中的自由场反应分析得到的地表时程，工程计算简化模型仍采用原地震波输入。

3 码头地震响应分析

3.1 模态分析

通过模态分析得到上述2种体系3种计算模型的前2阶固有频率，并分析其变化规律。为了考虑结构阻尼的影响，采用瑞雷阻尼并由前2阶频率值计算出相应的系数（表2）。

由表2可以看出，模型Ⅱ的基频最大，采用桩-土-码头结构模型和工程计算简化模型时，模型的基频将变小，周期变长，而且模型Ⅲ的基频要小于模型Ⅰ的基频。

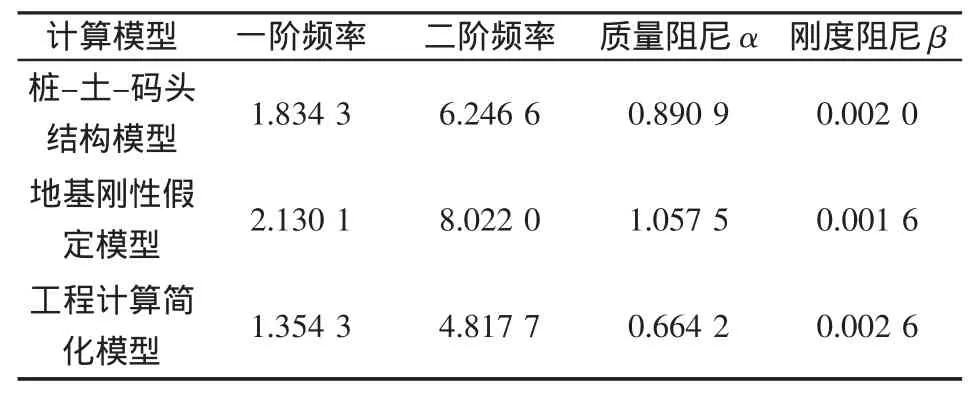
表2 模型的前2阶固有频率和瑞雷阻尼系数Tab.2 First and second natural frequencies and Rayleigh damping of the models

3.2 时程分析

为了方便比较，将考虑相互作用后码头的内力和变形与不考虑相互作用的情况下的比值（称为折减系数）作为分析指标，分别考察码头结构的最大水平位移以及主要立柱的轴力、剪力和弯矩的变化情况（表3及图2～图4）。

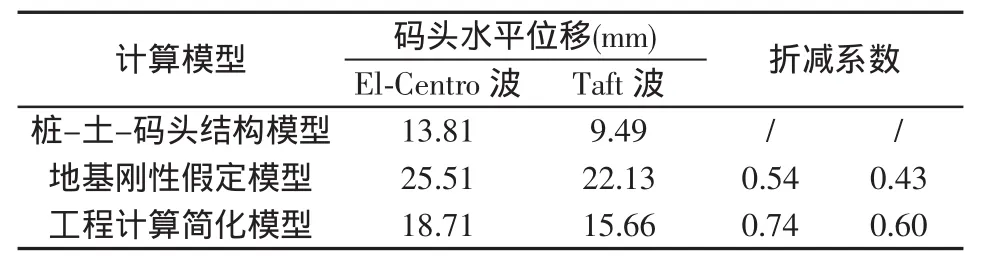
表3 码头各计算模型的水平位移值及折减系数Tab.3 Horizontal displacements and reduction factors of the models

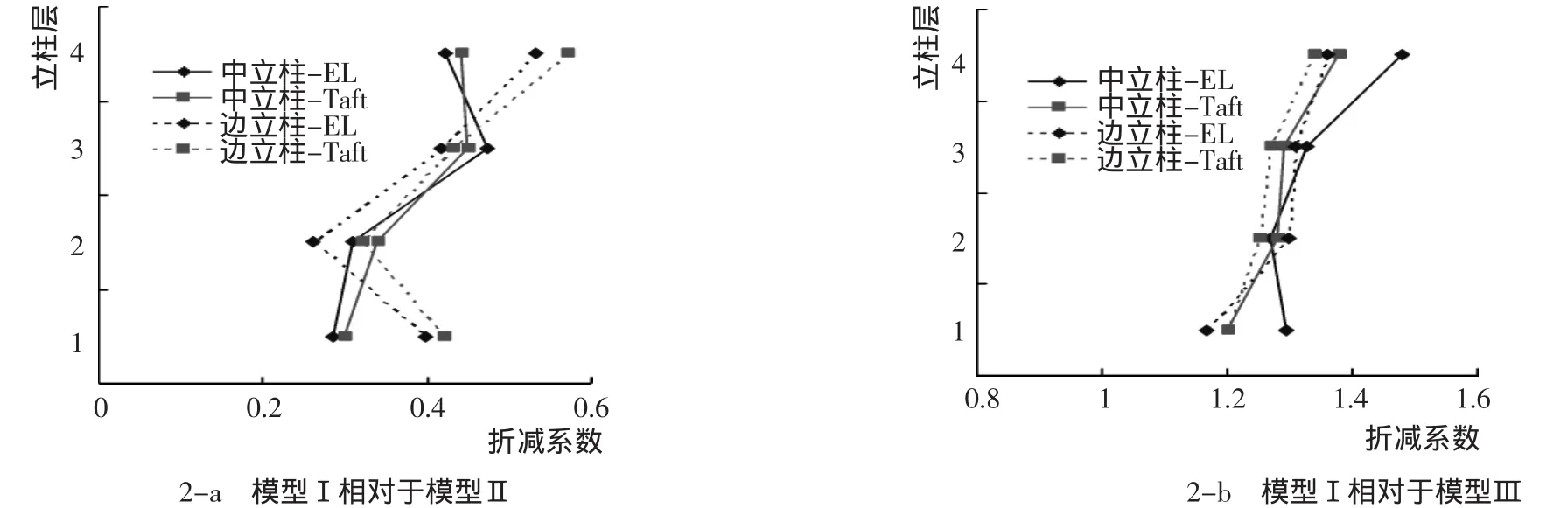
图2 立柱剪力折减图Fig.2 Shear reductions of column

图3 立柱轴力折减图Fig.3 Axial load reductions of column

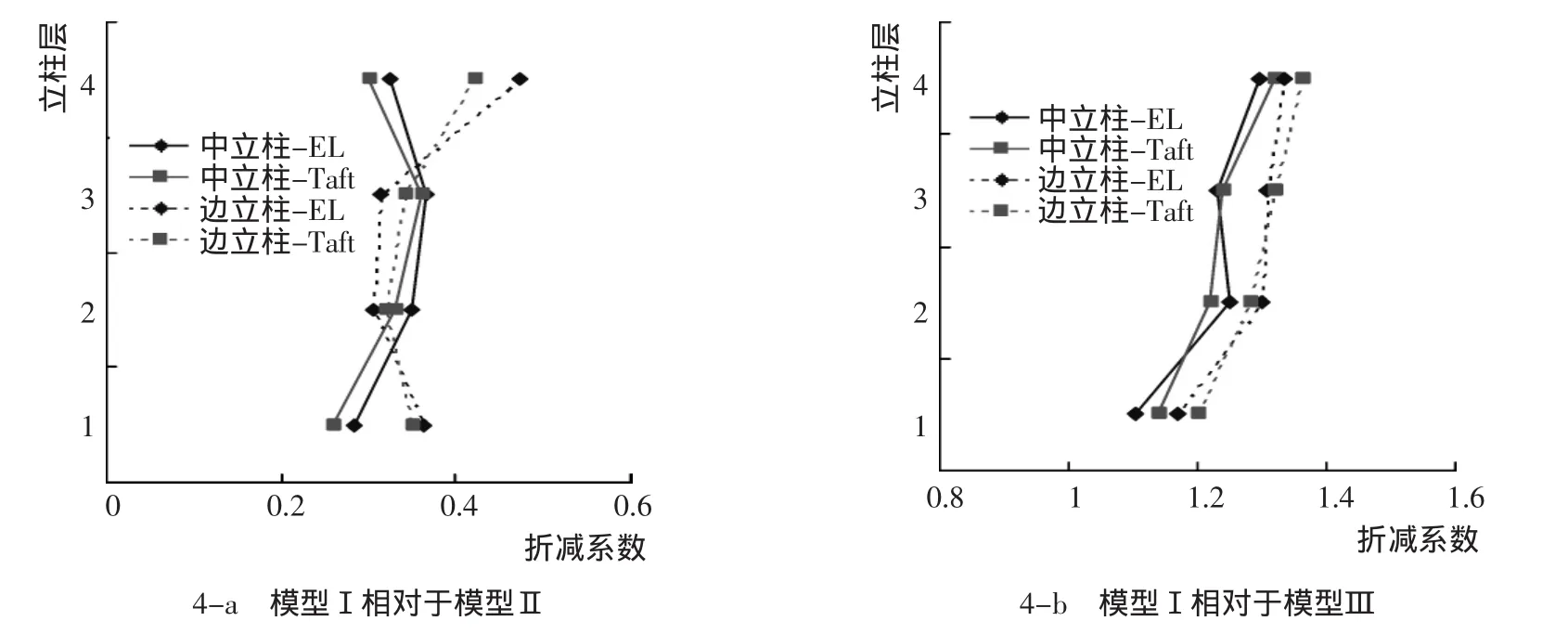
图4 立柱弯矩折减图Fig.4 Bending moment reductions of column

由图2可见，模型Ⅰ相对于模型Ⅱ的折减系数分布在0.25～0.60；对于中间立柱的剪力，下层立柱的折减比上层的大；对于两边立柱的剪力，中间层的折减比靠近底部和顶部的大。模型Ⅰ相对于模型Ⅲ的折减系数均大于1，其分布主要集中在1.3附近，而且下层立柱剪力的折减系数要比上层的小。由图3可见，立柱轴力峰值的折减系数均在1附近，并且在各层均匀分布。由图4可见，弯矩折减系数与剪力折减系数沿立柱层变化规律基本相同。

由表2可以看出，不同的地震波引起的水平位移的折减系数不同，但均小于1，并且模型Ⅰ相对于模型Ⅱ的折减系数要小于模型Ⅰ相对于模型Ⅲ的折减系数。模型Ⅱ的最大水平位移值大于模型Ⅰ的值，这是因为经过岸坡土体的自由场反应，放大了地震波，导致码头结构的水平位移相应变大；而模型Ⅲ的最大水平位移值也大于模型Ⅰ，但是通过前面的分析，其对应的弯矩值却小，这是因为框架码头的上部结构刚度大于桩基的刚度，码头结构的水平位移主要由桩基贡献，而由于岸坡的存在，模型Ⅰ桩基的自由长度变小、刚度变大，使码头在立柱内力变大的情况下，水平位移反而减小。

4 结论

通过上述对内河架空直立式码头的地震响应分析，可以得出如下结论：

（1）桩-土-码头结构模型的基频比地基刚性假定模型的基频小，比工程计算简化模型的基频大，所以当采用工程计算简化模型作为内河框架码头结构计算模型时，求解该计算模型的基本频率所得到的结果将小于实际值。

（2）桩-土-码头结构模型中立柱的位移、剪力和弯矩值比地基刚性假定模型相应的计算值小，存在一定的折减规律，但是轴力值却基本不受影响；桩-土-码头结构模型中立柱的剪力和弯矩值比工程计算简化模型相应的计算值大，但是位移反而减小，轴力值基本不受影响。

（3）当采用工程计算简化模型，对内河码头岸坡土体覆盖层较厚地区的集装箱码头结构进行抗震分析时，立柱剪力和弯矩计算结果比实际值要小，而位移值偏大，所以不建议采用该模型进行抗震分析，而改用桩-土-码头结构模型。

［1］李永梅，孙国富，王松涛，等.桩-土-杆系结构的动力相互作用［J］.建筑结构学报，2002，23（2）：75-81.LI Y M，SUN G F，WANG S T，et al.Dynamic Interaction of Pile-Soil-Frame Structure［J］.Journal of Building Structures，2002，23（2）：75-81.

［2］贾宏宇.框架集装箱码头结构抗震分析［D］.重庆：重庆交通大学，2009.

［3］郑子龙，郑昕阳.水运工程水下震动台的应用研究与进展［J］.水道港口，2010，31（3）：214-229.ZHENG Z L，ZHENG X Y.Construction and application of underwater shaking table for water transport engineering［J］.Journal of Waterway and Harbor，2010，31（3）：214-229.

［4］刘立平.水平地震作用下桩-土-上部结构弹塑性动力相互作用分析［D］.重庆：重庆大学，2004.

［5］杨小卫.桩-土-结构动力相互作用的数值分析［M］.武汉：武汉理工大学，2006.

［6］黄建勇，王多垠.内河架空直立式集装箱码头结构计算模型探讨［J］.水道港口，2008，39（1）：59-62.HUANG J Y，WANG D Y.Study on calculation model of inland river suspended vertical container terminal［J］.Journal of Waterway and Harbor，2008，39（1）：59-62.