商品供应链中修正模型研究

黄 凯

供应链通常是指企业通过对信息流、物流、资金流的控制，将供应商、制造商、分销商、零售商直到最终用户连成一个整体的功能链。在经济学上，供应链是由许多参与者组成的，这些参与者因为追求自身效用的最大化在供应链进行了一组交换。作为经济学分析的基本单元，新古典模型中对交换行为的解释是“边际效用的交换”，或者MU=P=MC。对于消费者而言，他支付的价格是他的效用损失，而他从购买的商品中获得的消费满足是他的效用获得；对于生产者而言，他生产商品投入的成本是效用损失，而出售价格则是对这种效用损失的补偿。最后交换在均衡点停止，形成稳定的供应链。

一.传统供应链模型及其不足

正如很多学者已经阐述的那样，新古典模型并不能完全解释交换行为，因为它有一个隐含条件：生产者和消费者具有完全相同的信息。委托代理的概念有助于我们从另一个角度观察，这就是经典的委托代理模型，因为模型中只有两个交易者，所以称为双主体模型。

1.经典委托代理关系-双主体模型

委托代理模型精确地描述了这样一类问题：存在两个参与者，一方是委托人，另一方是代理人，在供应链问题上，委托人是买主，代理人是卖主。买主的目标是促使卖主按照自己的利益选择行动，但是却不能直接观测到卖主选择的行动（或观测成本很高），只能观测到另外一些变量，这些变量是由卖主的行动与其它的外生随机因素共同决定的，所以只代表卖主行动的不完全信息。买主只能根据这些信息，用支付货币多少的行动来决定奖励或惩罚卖主，以激励其选择对买主最有利的行动。对于这种关系最一般模型为：

其中各符号的含义如下：

A：代理人所有可选择的行动的集合；

a：代理人选择的一个特定的行动 a∈A；

π：委托人所要求的结果变量，它具有可观测性，如产出、产品质量、委托者收益等等，π是代理人选择a和随机变量θ共同决定的，所以π可以被转换为一个随机变量；

s：委托人设计的交易合同，即委托人支付给代理人的报酬，或代理人收益；

v=v[π-s(x)]：委托人的VNM期望效用函数；

u=u[s(x)-c(a)]：代理人的VNM期望效用函数；

c=c(a)：代理人的成本函数，它是代理人选择a的函数，c′＞0 c＂＞0；

f(π，a)：与代理人选择的行动a相对应的随机变量π的密度函数；

使用一阶条件方法与拉格朗日方法整理得到传统模型的莫里斯·霍姆斯特姆条件：

因为μ≠0，这一条件说明委托人与代理人的边际效用之比不等于常数，不可实现帕累托最优风险分担。买主将根据商品质量观察代理人的真实努力程度而支付货币，所以卖主的收入决定于似然率，即买主的信心。

2.经典委托代理模型存在的不足

随着社会分工的深入，一个消费者可以委托中介去代替他完成购买，如果越来越多的消费者都委托同一个代理人完成购买，一个专业的代理机构就分化出来了，于是，在产业链上生成了一个无法被合并在“买主”或“卖主”的新的环节，这样双主体的经典模型就不适用了。

在现实生活中，的确大量存在这样一类参与者，他们担任商品交换的中间环节，并为商品在流通中追加价值，这类参与者可能是加工商、贸易商或仓储商等等，这是构成了供应链的必要条件，也是供应链不能用经典方式来解释的地方。例如，一个最简单的中间商，他只是从生产者手中购买到产品，然后销售给消费者。我们很难说这个中间商边际成本递增，因为大多数中间商进货成本随购买数量的增加而降低，我们也很难说这个中间商边际效用递减，因为中间商本人并不消费这些商品。更不用说很多中间环节担负着深加工、贴牌、包装、运输、存储、组合、分类等服务功能，兼生产与流通两种角色于一身，更加难以直接套用经典模型来解释。在分工高度发达的市场经济条件下，这种委托行为越来越复杂，经过的环节越来越多，供应链由此形成。

一旦最终消费者通过复杂的委托代理关系来购买一种商品，就产生了更加严重的信息不对称问题，供应链中的上下游参与者各自享有自己的私有信息，由于上游参与者的信息价值远大于下游参与者的信息价值，供应链参与者之间既有逆向选择，又有道德风险。逆向选择表现在代理人（上游参与者）拥有比委托人（下游参与者）更全面更准确的第一手市场信息；道德风险是委托人无法观测代理人的行动，上游参与者工作努力程度不能被观察到，且没有披露自己私有信息的意愿。下游参与者的效用程度取决于他制定的契约，信息的价值更多的体现在改善下游参与者的收益，这个过程经典模型是无法解释的。比如：

（1）大量存在的中间环节参与者，由于他们并不是商品的真正提供者，所以他们本身并不知道商品的真实质量水平，于是在中间商与消费者发生交易的时候，买卖双方都缺乏真实信息，那么这种交易将如何进行呢？

（2）如果在供应链上的一个环节发生了道德风险或是逆向选择，对整个供应链会有什么影响？

（3）买主试图利用货币奖惩来激励生产者提供高质量的农产品，但其货币去无法直接支付给该农产品的生产者，而是支付给了中间环节，买主的这一激励措施在传递中会被扭曲吗？

为了正确解释现代经济生活中大量通过供应链发生商品交换的现象，有必要对传统的委托代理模型进行修改，对中间环节的市场行为加以描述。

二、供应链委托代理模型的基本假定

在买方市场的条件下，商品和生产与流通都是以最终购买者的意愿为准，购买者的“货币选票”最终决定了所有参与者的行为，那么也可以这样来理解整个供应链的目标，即购买者效用的最大化。用信息经济学的角度来解释，买方掌握着“强制合同”：假定时间足够长，消费者总会了解到商品的真实质量水平q，并根据消费满足程度u(q)支付需求价格s[u(q)]。定义质量最优水平为q*，若消费者观察到商品的真实质量q＜q*，总可以制定出支付价格s[u(q)]＜s[u(q*)]，且若决定商品质量的原因除参与者的行为以外，还受到随机因素的影响，则q是一个随机变量，服从密度函数为f(q)的分布。这时强制合同表示为：∀q∈Q，即代理人只有提供最有利于消费者的质量q*，才有可能得到最有利于自己的价格s[u(q*)]。总之，若买方市场条件存在，供应链可以描述为连续委托代理关系，且最初委托人必然是货币持有者。或者说，买方市场是连续委托供应链模型的首要假定。

为了用委托代理关系把供应链模型化，还要做一些必要的假定：

1、单一商品假定。假定一个供应链只流通一种商品。如果一个供应链同时流通多种商品，则对消费者提供的效用分别是ui,i=1,2,…n。消费者分别支付需求价格s(ui)。数学上，可以解释为消费者获得总效用∑ui或者平均效用∑ui/n，这相当于把多种商品折合为一种“平均商品”。这样处理的好处在于，省略掉了各种商品之间的“替代”或“互补”关系对委托代理关系的干扰。

2、单位交易假定。假定商品流通的数量为一个固定数量。这是因为新古典经济学认为消费者对商品存在边际效用递减，通过固定交易数量来排除这一干扰，把交易数量定义为1个单位。

3、质量目标假定。假定商品质量是影响消费者效用的唯一解释变量。消费者对商品的评价是一个复杂的过程，其中很多是与经济活动无关的，比如风俗、偏好、广告等，但是这些因素与供应链无关，也应该排除在模型之外。按照这个假定，质量就是最初委托人追求的唯一效用来源，有：

三、供应链委托代理模型

如果这些假定成立，供应链可以用信息经济学的观点解释为：购买者作为最初委托人，通过流通环节的各代理人，把需求信息传递给最终生产者，并根据自己获得的效用，通过支付货币来实施奖罚，因此购买价格就成了第二参与者的效用获得。现实生活中，一般的消费品供应链通常是：

如上图，定义参与者Pi,i=1,…n，即有5个主体参与。其中P1是消费者，P5是生产者，Pi,(i≠1,5)是中间商，它的现实表现形式可能是加工厂、批发商、零售商或者同业协会等，Pi在第i个环节中是代理人，而在第i+1个环节中是委托人。

供应链的目标是消费者从商品消费中获得的效用，影响消费者效用水平的因素很多，从本文研究的目的出发，引入假定：商品质量q是影响消费者效用的唯一解释变量，q的解释变量包括随机因素θ和各参与者的努力水平ai，即：

一般来讲，消费者能观测到q的水平，但是观测不到各参与者的努力水平ai，那么在给定的质量水平(q＜q*)时，消费者无从判断这是由于随机因素θ（比如气候变化）还是努力水平不足(ai＜ai*)造成的，所以消费者只能根据自己的效用满足情况决定购买的价格水平pb。定义消费者效用获得是u(q)，若u(q)＞pb，或者消费者剩余 p1=u(q)-pb＞0时，消费者会发生购买行为。这样，购买价格实际是消费者效用剩余的函数p=s1[u(q)]。综上所述，供应链的目的是消费者剩余的期望值最大化，目标函数表示为：

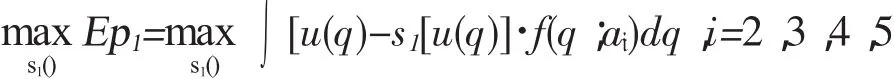
第二参与者（零售商）的效用p2来自于p1支付的s1[(u(q))，对第三参与者的奖惩合同是s2[s1()]。所以P2的期望效用函数 Ep2：s1[(u(q)]-s2(s1)-c2(a2)，其中 s1()是P1和P2的交易价格，c2(a2)是P2的努力成本；

第三参与者（批发商）P3的期望效用函数Ep3：s2(s1)-s3(s2)-c3(a3)；

第四参与者（总经销）P4的期望效用函数Ep4：s3(s2)-s4(s3)-c4(a4)；

第五参与者（生产商）P5的期望效用函数Ep5：s4(s3)-c5(a5)；s4(s3)相当于出厂价，而 c5(a5)相当于生产成本，按照经典理论的解释，当s4(s3)=c5(a5)时，即最后一个单位产品的边际成本等于销售价格时，生产商就停止生产。实际上，当两者的差小一个常数时5，生产就停止了，5被称为P5的保留效用水平。

综上所述，供应链中的委托代理模型是由一组参与者两两交易产生的委托代理链条。

四、供应链模型求解

在信息经济学中，最优合同取决于信息分布状态。传统模型中，当交易双方信息对称时，委托人用参与约束IC强迫代理人做出有利于自己的选择；而当信息不对称时，委托人应当使用激励相容约束诱导代理人做出有利于自己的选择。这一结论在供应链模型中同样适用，不同的情况是由于参与者众多，所以信息分布的类型更多。

1.信息对称型

供应链每个环节的委托人了解本环节的真实信息，此时，每一个环节都可以通过强制合同来消除激励相容约束。

（1）最初委托代理关系：

（2）中间委托代理关系：

由拉格朗日函数求取最优化一阶条件得：

（3）最终委托代理关系：

由拉格朗日函数求取最优化一阶条件得：

综合以上三点可知：供应链是委托代理中的一种特殊情况，其特点是在每一个环节的委托代理关系中遵循“边际替代率相等”的法则，也就是委托人与代理人的边际效用相同，或 λi＝1；i=1，2，3，4。在信息对称时，无论供应链怎样安排，都可以实现最优风险分担。为求取最优激励合同的条件，构造规划：

用拉格朗日函数求取最优化一阶条件得：

可见，在现实经济中，要形成一个健康的委托代理链关系，并不需要支付高昂的交易成本去构筑一个完全对称的信息链条，让买主知道整个供应的全部情况，只要每个参与者在本交易环节了解到充分的信息，就可以阻止代理人的道德风险。在满足委托人效用对代理人努力的边际期望水平等于代理人在报酬和努力边际成本之间的边际替代率条件下，委托代理链实现了最优激励。总之，实现各个环节的信息对称不是委托代理链管理的目标模式，所谓建立全统一的商品交易大市场也就是以此为目标的，显然这是一个具有重要现实意义的结论。

2.信息不对称型

由于某些环节的委托人不了解本环节的真实信息，只有结果变量q可以被观测到，所以委托人只能根据q来制定奖惩函数。此时，这些环节必须建立激励相容约束。用规划的形式表现为：

（1）如果不对称信息发生在最初环节：

根据莫里斯·霍姆斯特姆条件，使用一阶条件方法与拉格朗日方法整理得：

若μ≠0，信息不对称条件下单调似然函数是线性的，或者说，在委托人认看来，代理人的努力水平与可观测变量的提高是同比例增长的。在信息不对称条件下，以发生信息不对称的环节为界，委托代理链分成三段，这样做同样也有助于简代求解。如下图：

对以上委托代理链分三段求解，对于左侧的“非激励相容及附加约束段”，可用由拉格朗日函数求取最优化一阶条件得：

对于右侧的“非激励相容约束段”，也可用由拉格朗日函数求取最优化一阶条件得：

对于中间的激励相容约束段{Qk+1,Pk+2}：它相当于一个经典的信息不对称条件下的解，它的数学表达式为：

其中IA为附加约束条件，它的含义是在参与者P1,P2,…Pk,Qk+1之间合理的分配。上式的求解过程分成两步：

第一步，只考虑目标函数和参与约束IC，上式等价于：

仍由拉格朗日函数求取最优化一阶条件得：

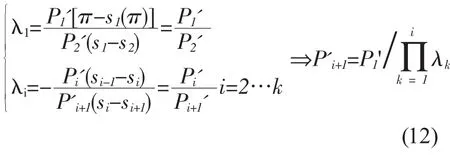
第二步，考虑附加约束条件IA，opt[s1(π*)-s1(π)；P1,P2,…Pk,Qk+1]，按照微观经济学弹性与效用分摊原理，不难得知联立方程组：

其中△pi代表第i个参与者分摊的负效用，Ei可以理解为第i个参与者的可观测变量π对效用的弹性。

可见，由于委托代理双方都处于信息劣势造成的可观测目标变量的损失π*-π是由激励兼容约束段的所有参与者共同分担的，其分担比例决定于效用弹性之比。

式（14）以隐函数的方式定义了信息对称情况下的最优合同。

五.结 论

本文证明了：商品供应链所代表的委托代理关系，并不是经典委托代理关系的简单迭加，而是一类新的扩展类型。信息结构对商品供应链有着重要的影响。因此，改善信息状况可以很大程度规范商品供应链，消除逆向选择。由于商品供应链主体众多，这类模型的求解方法比两个主体构成的经典模型要复杂得多，由于篇幅的限制，本文还不可能把参与者的风险态度、相互之间的效用影响纳入其中，这一领域还有巨大的研究潜力和研究价值。

［1］张维迎.博弈论与信息经济学[M].上海：上海三联书店，2004.

［2］韩建新.信息经济学[M].北京：北京图书馆出版社，2000.

［3］罗荣桂.张光明.非对称信息条件下的委托一代理模型及风险分析[J].武汉理工大学学报(社会科学版),2005,(6):362-365.

［4］马费成.龙鹜.不完全信息与非对称信息[J].情报理论与实践,2003(1):93-96.

［5］张爱，袁治平，张清辉.供应链企业委托代理问题的研究[J].工业工程与管理，2003,(3):52-55.

［6］杨治宇，马士华.供应链企业间的委托代理问题研究[J].计算机集成制造系统，2001，7(1)：19-22.

［7］Stigler,G.J.The economics of information.[J].Journal of Political Economy,1961(69):213-285.

［8］Rahi and Rohit.Optimal Incomplete Market with Asymmetric Information.[J].Journal of Economic Theory ,1995:65-67.

［9］Ha A.Supplier—buyer contracting：Asymmetric cost information and cut of level policy for buyer participation[J].Naval Re.arch Lagisties，2001(48)：41—64.

［10］Akerlof,G.A.The market for`lemons':Quality uncertainty and the marketmechanism.[J]AQuarterly Journal of Economics.1970(84):488-500