基于PCA-SVMR快速测定复方氯丙那林和对乙酰氨基酚

郭嘉伟，谢洪平

（1.第三军医大学药学院，重庆 400038；2.苏州大学药学院，江苏 苏州 215123）

1 引 言

近红外光谱（NIRS）分析方法是一种便捷、快速、无污染的分析测试技术，通过多元校正模型可实现多组分快速同时测定[1-2]。其关键技术环节之一是建立量测数据的校正模型，而常用的方法有多元线性回归、逐步回归、主成分回归和偏最小二乘（PLS）等[3]。这些方法均是建立在大量分布均匀的已知样本基础之上的传统的统计学习方法，然而，在实际的分析工作中往往难以获取大量的已知样本，同时，近红外数据与组分浓度间常呈现非线性映射关系，因此近红外光谱小样本体系的非线性建模方法将成为人们关注的问题[4-5]。建立在统计学理论基础上的支持向量机（Support Vector Machine，i.e.SVM）算法[6-7]可以有效地解决小样本体系的非线性建模的准确度问题，该类问题在药物复方制剂以及生产过程的快速测定中更为突出。《中国药典》对复方氯丙那林和复方对乙酰氨基酚两种制剂均难于实现多组分快速同时测定[8]，该文将以主成分分析（PCA）为基础，结合SVM回归（SVMR）即PCA－SVMR方法对该两类制剂在小样本情况下的快速测定方法进行研究，并对PCA-SVMR法在药物复方制剂中的应用进行方法学考察。

2 SVMR基本原理[9-11]和PCA-SVMR方法

统计学理论将通过使结构风险最小化来逼近实际风险，即控制函数集的复杂度使回归函数最平坦，等价于最小化若允许存在拟合误差（即引入松弛因子与，即式（1）为：

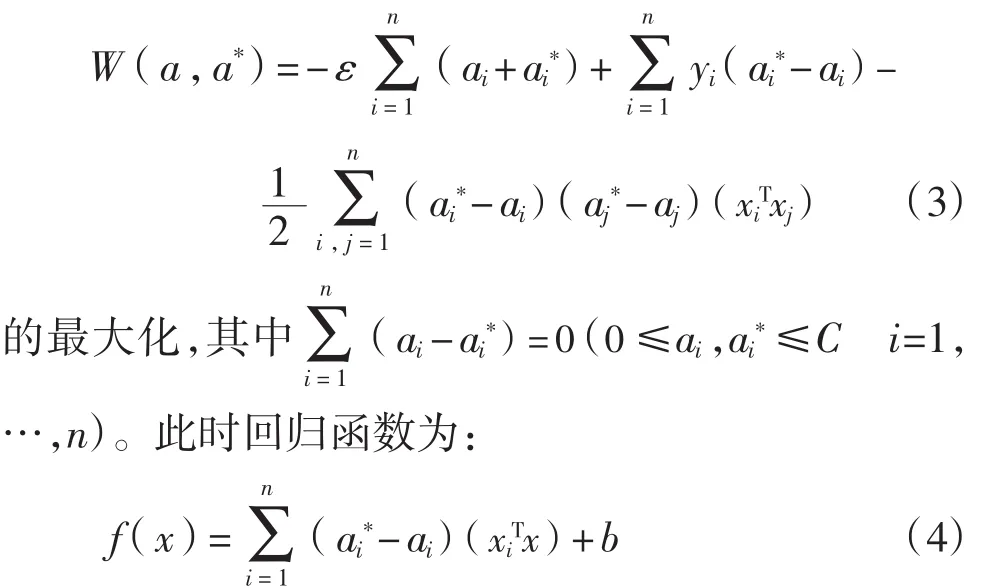
对于非线性映射，可以用泛函理论中满足Mercer条件的一种核函数K（xi·xj）将低维空间的非线性问题转换为高维空间中的线性问题，即式（3）和式（4）中在低维空间中的内积（xiT·xj）将用高维空间中的内积运算K（xi·xj）代替。其中SVM使用的核函数主要有多项式、径向基和Sigmoid等3种形式。

由于NIRS的量测信号较弱，干扰信号相对增强，特别是复方药物制剂中存在的多种有效组分和辅料将对被测组分构成严重的信号干扰，使多元校正模型的预测能力降低，在小样本体系中该类现象将更为突出。为了解决此问题，该文将以PCA方法提取其有用量测信息，再以SVMR方法建立其多元校正模型（即PCA-SVMR法）。

3 实 验

3.1 仪器与试药

傅里叶变换NEXU红外光谱仪（美国Thermo Electron公司），配有积分球漫反射采样系统。复方氯丙那林的试药：盐酸氯丙那林（纯度99.95%，浙江万邦药业有限公司），盐酸溴己新（纯度99.62%，浙江万邦药业有限公司），盐酸去氯羟嗪（纯度99.52%，上海大众制药厂），辅料硬脂酸镁和淀粉为药用规格，所有药品均由苏州第三制药厂有限责任公司提供（批号：20050412）。复方对乙酰氨基酚的试药：对乙酰氨基酚（纯度99.73%），阿司匹林（纯度100.28%），咖啡因（纯度99.38%），辅料柠檬酸、硫尿和淀粉均为药用规格，所有药品均由苏州第一制药厂提供（批号：20050209）。

3.2 采集样品的NIR光谱

分别将样品粉末直接装入普通玻璃瓶中，利用积分球漫反射采样系统测定其NIR光谱。光谱采集条件：以金箔为背景，波数范围10000～4000cm-1，分辨率8cm-1，扫描次数64次，每个样本以3次实验的平均光谱作为样本光谱，以吸收光谱的形式反映样品组分漫反射光谱的强度。

4 结果与讨论

4.1 样本的设计与制备

为了让定量模型能够有效地应用于实际的复方制剂样本和对PCA-SVMR方法在复方制剂中的应用进行方法学研究，以在复方氯丙那林胶囊和复方对乙酰氨基酚片法定合格含量标准的基础上并且适当增加可测定范围为原则，设计了建立两种制剂的含量测定模型的样本集。每类样本集包含了含量分布均匀的样本，其中，复方氯丙那林胶囊（30个样本）为：盐酸氯丙那林2.80%～4.37%、盐酸溴己新4.04%～9.91%和盐酸去氯羟嗪12.60%～19.91%；复方对乙酰氨基酚片（29个样本）：对乙酰氨基酚25.91%～58.29%、阿司匹林16.05%～28.45%和咖啡因3.59%～6.38%。该文对每类制剂的样本集中所含的三种有效组分的浓度变化方式进行了非线性设计，以使样本间保持线性独立。

4.2 数据处理方法

为了建立两种制剂的NIRS多元校正模型，所采用的SVM算法软件为网络共享Libsvm软件（由Chang Chih-chung和Lin Chih-jen提供），该文采用了在MATLAB环境下运行的Libsvm-MATLAB软件，而PCA-SVMR软件则在SVM软件的基础上由本实验室完成。PLS算法的相应软件以及预处理软件均由本实验室在MATLAB（V6.0）环境下编制。

4.3 光谱预处理与富信息光谱波段选择

在无信号波段明显发生了基线漂移，将导致量测数据不能准确反映组分的浓度变化，该文以无信息区间为基础采用基线平移的方法消除其光谱漂移。

对于波段的选择，既要保证模型有较好的拟合能力，更要保证模型有较强的预测能力，研究发现以PLSR方法确定的校正集的交互检验的根均方差（RMSECV）最小为标准所选择的光谱波段，具有最小的预测误差。基于此确定了两个样本集的富信息光谱波段为：复方对乙酰氨基酚片中有效组分对乙酰氨基酚为 7250～7450cm-1和 8600～8980cm-1、阿司匹林 5765～5915cm-1和 6110～6415cm-1、咖啡因 7 940～9620cm-1；复方氯丙那林的三个有效组分均为4000－10000cm-1。

4.4 建立PCA－SVMR多元校正模型

在没有先验知识的情况下，用径向基函数作为核函数往往能够得到较好的拟合结果[1]，故选择常用的径向基函数K（x，为核函数[6]。SVMR模型的3个参数误差精度ε、正则化系数C和径向基核函数的宽度σ以模型的预测平方相关系数最大为标准，采用全局优化的方法确定。

为了对PCA-SVMR方法所对立的模型进行方法学考察，选择了两种制剂分别建立PCA-SVMR和PLSR多元校正模型。在样本集中以被测组分的浓度分布均匀为原则，随机地将其分为校正集和预测集，其中复方氯丙那林的校正集和预测集分别为22和8、复方对乙酰氨基酚则为21和8。利用PCA-SVMR方法建立多元校正模型，其模型参数见表1和表2。

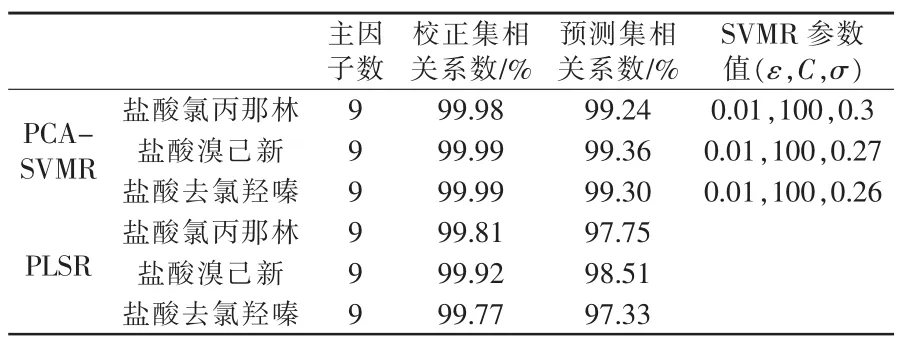
表1 复方氯丙那林胶囊的PCA-SVMR和PLSR模型

表2 复方对乙酰氨基酚片PCA-SVMR和PLSR模型

4.5 PCA-SVMR方法与PLSR法的比较研究

为了对PCA-SVMR方法在药物复方制剂中的多组分快速分析测定的特征进行方法学考察与研究，以两种模型制剂复方氯丙那林与复方对乙酰氨基酚分别考察了该方法与传统的稳健方法PLSR所建立的多元校正模型的模型特征和模型测定的准确度（表1和表2）。为了使两种方法具有可比性，它们均采用了相同的富信息光谱区间和主因子数。从表1和表2可知：PLSR方法具有较强的拟合能力，且强于预测能力，但预测能力严重依赖于其拟合能力的强弱，高预测能力的前提是模型必须具有高拟合能力，并且模型的预测稳定性也与其拟合样本的统计特征特别是分布均匀性存在很强的相关性，建立模型所选样本的代表性即成为模型预测能力强弱的重要因素或决定因素；对于PCA-SVMR方法，高预测能力并不一定需要高拟合能力为保障，复方氯丙那林的拟合能力略强于预测能力，而复方对乙酰氨基酚的预测能力却大大强于拟合能力，并且总体上两种模型制剂的预测能力优于PLSR。由于具有这样的特点，使基于传统统计学方法的PLSR在药物小样本体系中表现出了不稳定的特征，此时PCA-SVMR方法却具有明显的优势。这样的特征在药物生产和临床药学中显得尤为重要，因此该方法在药物分析中将具有重要的应用价值。

[1]瞿海斌，刘晓宣，程翼宇.中药材三七提取液近红外光谱的支持向量机回归校正方法 [J].高等学校化学学报，2004，25（1）：39-43.

[2]Baratieri S C，Barbosa J M，Freitas M P，et al.Multivariate analysis of nystatin and metronidazole in a semi-solid matrix by means of diffuse reflectance NIR spectroscopy and PLS regression[J].Journal of Pharmaceutical and Biomedical Analysis，2006（40）：51-55.

[3]刘平年.PLS法和PCA法在近红外光谱定量分析中的应用研究[J].广州食品工业科技，2004，20（4）：106-107，134.

[4]Pérez-Marín D，Garrido-Varo A，Guerrero J E.Nonlinear regression methods in NIRS quantitative analysis[J].Talanta，2007（72）：28-42.

[5]Chauchard F，Cogdill R，Roussel S，et al.Application of LS-SVM to non-linear phenomena in NIR spectroscopy:development of a robust and portable sensor for acidity prediction in grapes[J].Chemometrics and Intelligent Laboratory Systems，2004（71）：141-150.

[6]Vapnik V N.The nature of statistical learning theory[M].北京：清华大学出版社，2000.

[7]张学工.关于统计学习理论与支持向量机 [J].自动化学报，2000，26（1）：32-42.

[8]国家药典委员会.中华人民共和国药典（二部）[M].北京：化学工业出版社，2005.

[9]康宇飞，瞿海斌，沈 朋，等.预测毛吸管带电泳有效淌度的支持向量回归建模方法[J].分析化学，2004，32（9）：1 151-1155.

[10]David Sanchez A V.Advanced support vector machines and kernel methods[J].Neurocomputing，2003（55）：5-20.

[11]王定成，方廷健，唐 毅，等.支持向量机回归理论与控制的综述[J].模式识别与人工智能，2003，16（2）：192-197.