傅里叶级数图案设计初探

李雪枫,袁涛

(昆明理工大学机电工程学院,昆明650093)

艺术与数学有着极其丰富的普遍意义和极其深刻的美妙联系.多少世纪以来,艺术家在进行艺术的创作中,利用数学原理和数学方法而使画面充满了和谐与美感.古希腊雕塑家们曾把黄金分割用在他们的许多作品的比例中.伟大的达◦芬奇在其绘画研究中运用黄金矩形、比例和射影几何,取得了非凡的成就.今天,数学在为艺术家提供创造和传达他们思想的灵感和工具方面仍然起着积极的作用.艺术家利用数学思想创造更深邃的艺术.事实上,有很多艺术家正在进行与数学思想——多维空间和计算机再现技术的数学思想有关的艺术探索.

数学(特别是现代数学)的研究对象在很大程度上可以被看成是“思维的自由想象和创造”.因此,美学的因素在数学的研究中占有特别重要的地位,以致在一定程度上数学就可被看成一种艺术.数学理论以逻辑的严密性和规律性,在艺术的领域里借助于直觉、想象等非逻辑思维.提出新的概念和理论.所以,数学不仅有利于发展人们的逻辑思维,而且也有利于在人们的创造活动中对审美、直觉的发展.

近代计算机技术更是将数学与美术这两者紧密地结合起来,形成了一门崭新的边缘学科--数学美术学.1980年当计算机的图形功能日趋完善的时候,数学公式所具有的美学价值被曼德布尔鲁斯所发现①,这就打开了数学美术宝库的大门,使常人也有幸目睹了数学公式所蕴藏的美学内涵.由一些简单的数学公式经过上亿次迭代计算所产生的数学美术作品,可以用电脑根据实物自行改变大小进行组合形成局部图案,再自动拓展设计出复杂的图案,广泛用于印染、针织、装潢.许多复杂的绘制过程和难以得到的视觉效果,在电脑中变得轻而易举.

1 傅里叶级数及其展开图的绘制

1.1 傅里叶级数的概念

傅里叶级数原来主要应用于信号分析.自然界中周期现象的数学描述构成周期函数.傅里叶级数反映了一个周期函数可以分解为有限或无限多个不同频率的正弦(或余弦)信号之加权这样的一个基本事实,同时也说明了无限多个不同频率的正弦(或余弦)信号可以合成某一指定的周期信号.

下面是傅里叶级数的概念:

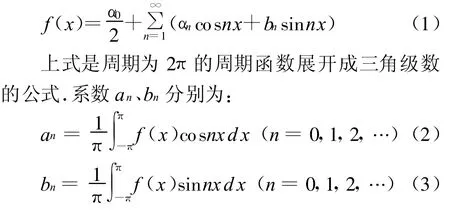
1.2 傅里叶级数图形的绘制

图2 是以上代码中在区间上的傅里叶展开图.

图1 级数图形

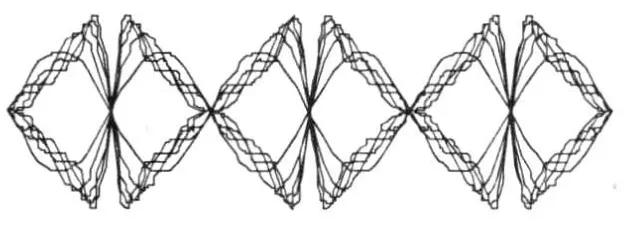
图2 不同区间的级数图形

通过以上一个简单的例子,我们可以看出:傅里叶级数图形非常具有节奏韵律感,并且,当改变变量的取值范围,就可以生成重复的、变化的图案,由此得到变化的单元及重复的有节奏的构图.

2 傅里叶级数图形在图案设计中的应用

2.1 傅里叶级数图形的形态特征

由于三角级数的周期性,傅里叶级数图形具有反复出现的形态特征,并且在反复的同时兼有大小的变化、高低的起伏,因而傅里叶级数图形具有强烈的节奏与韵律感,如图3所示;

傅里叶级数图形在构图上是对称、平衡的图形.如图4,这是一个完全对称、平衡的图形,结构规则,平稳统一,在视觉心理上偏于严谨和理性.我们在图案设计中采用这些形式能使图案产生安静、平稳和庄重之感.

图3 级数图形的节奏韵律

图4 级数图形的对称平衡

2.2 应用傅里叶级数进行图案设计

图案纹样的构成形式可分为独立式和连续式两类.独立式受外形左右,分为单独纹样和适合纹样;连续式多分为二方连续和四方连续等综合纹样.

(1)单独纹样图案的设计

单独纹样是图案组织中最基本的形式,由它进行组合、排列或者发展、衍生,可构成丰富的图案变化.当然,它可以进行正负形态的变化、或者比例变形.因此,又被称为基本形.单独纹样的应用范围很广泛:室内的装饰浮雕、壁饰、椅子背、服装的前身、领角、领带及皮包、发卡等;纺织品的床单、毛巾、手绢等以及在器物上.

图5 基本形1

图6 单独纹样1

图7 单独纹样2

图5 是傅里叶级数基本形.

图6 是将此基本形导入CorelDRAW软件中经90°旋转变化得到的单独纹样.

图7 是同一基本形在CorelDRAW软件中经逻辑运算设计得到的单独纹样.

(2)二方连续图案的设计

二方连续纹样是通过基本形的线型排列所形成的,是一种具有连续性的纹样图形.通常连续展开于左右(横)或上下(纵)两个方向.二方连续纹样主要应用在:地毯、瓷砖、墙线装饰、铁艺栏杆;纺织品桌布、床单边饰及各种装饰布边;盆边、碗边、碟边,还有服装衣摆、围巾边饰、挂包等等.

图8 是由与图5相同的基本形1创作出的二方连续纹样.将傅里叶级数基本形导入CorelDRAW软件中经旋转、拼接、翻转设计变化而来.

图8 二方连续纹样

(3)四方连续图案的设计

四方连续纹样是通过基本形的面型排列所形成的连续纹样.四方连续纹样适合于大面装饰,如纺织品、壁纸、建筑纹样、地砖等.

图11是由基本形2(图9)和单独纹样3(图10)共同创作出的四方连续纹样.

3 结 语

通过以上设计实例可以看出:傅里叶级数图形本身就具有很强的节奏性和美感.应用傅里叶级数的基本形、变体和其组合,创作出的图案体现出对称与平衡、节奏与韵律、变化与统一等形态特征.通过不同的构图方法,相同的基本形可以产生出多种纹样图形,并且创作出的图案形象丰富,图为形,地亦为形,图地互换,形成正负形态.傅里叶级数形成的图形具有强烈的数理关系和非人为的因素,其原始图形揭示了设计艺术形式规则中的数理内涵,也为设计艺术增添了理性化的表达方式,并在形态的创造方面赋予设计师更广阔的空间.

[1]张维忠.文化视野中的数学与数学教育[M].北京:人民教育出版社,2006:31-33.

[2]徐人平.设计数学[M].北京:化学工业出版社,2006:152-153.

[3]何 洁.数字图形构成[M].北京:清华大学出版社,2006:32-35.

[4][日]雨宫好文,佐藤幸男.信号处理入门[M].北京:科学出版社,2000:11-12.